基于贝叶斯平滑转移模型的汇率非线性协整关系研究

朱慧明， 周 峰， 曾昭法， 李 荣， 游万海

(1.湖南大学 工商管理学院,湖南 长沙 410082； 2.湖南大学 金融与统计学院,湖南 长沙 410079)



基于贝叶斯平滑转移模型的汇率非线性协整关系研究

朱慧明1， 周 峰1， 曾昭法2， 李 荣1， 游万海1

(1.湖南大学 工商管理学院,湖南 长沙 410082； 2.湖南大学 金融与统计学院,湖南 长沙 410079)

针对平滑转移模型参数估计不确定性导致的协整检验方法相对复杂问题，提出基于平滑转移模型的贝叶斯非线性协整分析。通过模型的统计结构分析，选择参数先验分布，结合参数的后验条件分布特征设计Metropolis-Hasting-Gibbs混合抽样方案，据此估计平滑转移模型的参数，并对回归残差进行贝叶斯单位根检验，解决参数估计过程中遇到的参数估计不确定性及协整检验复杂的问题；利用人民币对美元汇率与中美两国的利率数据进行实证分析。研究结果表明：MH-Gibbs抽样方案能够有效估计平滑转移模型的参数，中美汇率波动和利差之间存在平滑转移协整关系。

平滑转移模型；非线性协整；贝叶斯分析；MH-Gibbs抽样；汇率波动

0 引言

协整是由Engle和Granger[1]首次提出的，主要是用来描述经济与金融系统中非平稳同阶单整变量间的长期均衡关系。在经济时间序列协整关系的研究过程中，线性协整关系检验通常假定变量之间的长期均衡关系是线性的。但实际上，宏观经济与金融时间序列经常呈现非线性与非对称的特性。自从Balke等[2]首次采用门限机制转换模型有效地刻画变量之间的非线性，非平稳特性,研究金融时间序列非线性特征的协整模型逐步得到扩展，例如，门限机制协整模型(TR)，马尔科夫机制转换协整模型(MSR)，平滑转移机制协整模型(STR)。TR和MSR模型都是描述变量之间非连续跳跃间断的转换关系，而实际许多经济现象的转换机制是连续且平滑的，例如经济周期波动[3]和汇率波动[4]。Granger 和Teräsvirta[5]以及Teräsvirta等[6]提出了平滑转移回归模型并运用拉格朗日乘数(LM)检验模型的线性特征。Choi和Saikkonen[7]将非平稳时间序列线性协整关系推广到平滑转换协整，提出了协整Logistic平滑转移回归模型，文中采用Gauss-Newton方法估计模型参数，发现参数估计的偏差较小，并构造LM估计量检验协整向量的非线性，但估计量是一致但有偏的，因此不适合作假设检验。Kapetanios[8]构建了平滑转移误差修正模型，并通过使用泰勒展开式近似检验非线性。平滑转移模型在经济金融中，通过连续的转移函数，阐述变量之间的连续的变化关系，从而在金融、经济、能源等领域得到广泛的应用。Serra等[9]使用平滑转移误差修正模型拟合美国市场的玉米，乙醇，原油与汽油价格之间的关系，发现能源价格与粮食价格存在长期稳定的非线性关系。彭方平等[10]研究发现通货膨胀预期对我国货币政策有效性的影响呈现非线性和非对称的特征，货币政策效果在高低两个区制下是不同的。Ben Cheikh[11]和Béreau[12]通过研究得到结论，由于交易成本的存在，汇率波动机制呈现出平滑转换特征。

然而，在进行平滑机制检验时，转移参数在线性协整的原假设下是无法识别的，因此，检验统计量里包含控制转移状态的冗余参数。常用的多项式近似估计法和非线性最小二乘法存在参数估计不准确，有偏的问题, 并且假设检验统计量的统计性质未得到完全验证。贝叶斯分析方法在平滑转换模型参数估计与假设检验上的应用，避免了上面的一些问题。首先，模型结构的非线性变化并不影响参数后验分布的取得，即在非线性模型下贝叶斯分析方法同样可以适用；其次，运用贝叶斯分析方法估计平滑转换回归模型参数，解决了非线性最小二乘估计方法下参数估计有偏，难以收敛的问题。因此，在平滑转移回归模型中应用贝叶斯分析方法具有理论与现实意义，逐步得到学者的重视。(近年来，Wang和Holan[13]对平滑转移模型进行了贝叶斯分析，但未涉及到变量间协整关系的分析。Gefang[14]对Logistic型平滑转移误差修正模型进行贝叶斯推断，得到了冗余参数的后验分布，并研究了战后英国货币供给与产出之间的关系，结果表明两者存在长短期非线性调整关系；然而，该文主要是在假设变量间存在协整关系的前提下利用贝叶斯方法估计平滑转移误差修正模型，可能导致变量之间存在伪回归问题。因此，平滑转移协整检验的贝叶斯研究还有待进一步完善，通过设计协整检验过程，精确估计模型参数，从而获得有效的平滑转移协整检验方法。

本文结合贝叶斯方法和平滑转移模型构建贝叶斯平滑转移模型，据此研究贝叶斯平滑转移协整检验方法。通过MH-Gibbs混合抽样方法，有效估计平滑转移模型参数，解决参数估计不确定性问题；同时，结合MCMC抽样方法研究回归残差的平稳性，进行平滑转移协整关系的推断；并利用中美汇率波动和中美利差序列进行贝叶斯平滑转移协整的实证分析。

1 贝叶斯平滑转移协整模型构建

1.1 平滑转移模型结构分析

平滑转移模型扩展了门限模型，在描述长期均衡关系上进行了平滑转移的调节。平滑转移回归模型如下:

yt=μ1+β1xt+(μ2+β2xt)F(xt;λ1,λ2)+εt,t=1,2…T

(1)

此处，xt,yt都是一阶单整变量，误差项εt为一个高斯白噪声过程，且相互独立，εt～N(0,σ2)，转移函数有以下两种形式，分别是Exponential和Logistic型[15]，即

F1(xt;λ1,λ2)=1-exp(-λ1(xt-λ2)2)

(2)

F2(xt;λ1,λ2)=1/(1+exp(-λ1(xt-λ2))

(3)

其中，转移参数λ1控制转移的速度，满足λ1>0，λ2为位置参数。Exponential转移函数(2)表示对称的三机制(regime)平滑转移情形，对于给定的(λ1,λ2)，β1表示中间机制的系数，β1+β2F(xt;λ1,λ2)是两尾机制系数。当λ1增大时，模型在三机制之间的转换加快，当λ1=0时，只存在中间机制，当λ1→∞时，模型转化为线性形式。Logistic型转移函数(3)表示了两机制转移。当λ1=0，模型转化为线性形式；当λ1→∞时，转移函数退化为示性函数I(xt>λ2)，模型变为门限形式。当xt>λ2时，F(xt;λ1,λ2)=1，当xt<λ2时，F(xt;λ1,λ2)=0。

1.2 模型参数的贝叶斯分析

令y=(y1,y1,…,yT)′，e=(1,1,…,1)′，e是长度为T×1的列向量，x=(x1,x1,…,xT)′，F=diag(F(x1;λ1,λ2)，F(x2;λ1,λ2)，…F(xT;λ1,λ2))，ε=(ε1,ε2,…,εT)′，θ=(μ1,β1,μ2,β2)′，z=(e,x,Fe,Fx)，那么，平滑转移模型(1)可简化为：

y=zθ+ε,ε～N(0,σ2I)

(4)

其中，I为T×T的单位阵，则y～N(0,σ2I)，相应地，平滑转移回归模型的似然函数为：

(5)

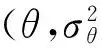
(6)

此处IG表示逆Gamma分布，G表示Gamma分布。

根据贝叶斯定理，通过参数的先验概率密度和似然函数的乘积可以得到平滑转换回归模型参数的联合后验概率密度函数。即

π(θ,λ1,λ2,σ2|Data) ∝L(θ,λ1,λ2,σ2|Data)π(θ,λ1,λ2,σ2)

∝L(θ,λ1,λ2,σ2|Data)π(θ)π(λ1)π(λ2)π(σ2)

(7)

由于参数的联合后验分布形式比较复杂，无法对其进行直接抽样，为了能够运用MCMC抽样算法，下面讨论模型参数的完全条件后验分布与贝叶斯估计：

(1)θ的完全条件后验分布。由贝叶斯条件概率的定义，参数θ的完全条件概率密度为

π(θ|Data,λ1,λ2,σ2) ∝π(θ,λ1,λ2,σ2|Data)/∫π(θ,λ1,λ2,σ2|Data)dθ

(8)

显然，θ的完全条件后验分布为正态分布，即

(9)

(2)σ2的完全条件后验分布。同样地，由条件概率的定义，参数σ2完全条件概率密度为

π(σ2|Data,θ,λ1,λ2)∝π(θ,λ1,λ2,σ2|Data)/∫π(θ,λ1,λ2,σ2|Data)dσ2∝(σ2)-a-1exp(-b/σ2)

(10)

其中，a=T/2+a0,b=b0+(y-zθ)′(y-zθ)/2。

显然，σ2的完全条件后验分布为逆Gamma分布，即

(σ2|Data,θ,λ1,λ2)～IG(a,b)

(11)

(12)

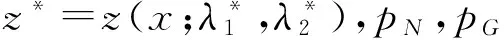
1.3MH-Gibbs混合抽样

根据以上的完全条件后验分布，利用Gibbs抽样方法进行抽样，同时在过程中嵌入Metropolis-Hasting算法对参数λ1,λ2进行抽样。此时MH-Gibbs混合抽样按下面的步骤进行：

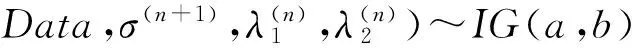
2 协整回归残差值平稳性的贝叶斯分析

2.1 单位根检验模型构建

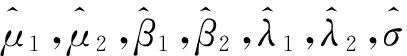
(13)

(14)

(1)ρ的后验分布。由条件概率的定义，

(15)

(16)

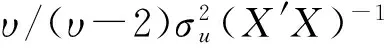
(17)

此处，b1为向量b中的第一个分量，a11是矩阵(X′X)-1中的第一个对角元素。

(18)

2.2 残差平稳性的贝叶斯检验

在贝叶斯理论框架中，贝叶斯因子是进行假设检验与模型选择的重要工具。若存在两个假设可供选择，利用现有数据进行假设检验，就需要用到贝叶斯因子。基于以上的残差回归模型，设原假设H0:|ρ|<1与备择假设H1:|ρ|>1,进行假设检验。模型中ρ为均匀分布，故用于检验的贝叶斯因子可以简化为：

(19)

若K01远大于1，则原假设不被拒绝，即表明残差序列是平稳的，否则就拒绝原假设H0,此时说明残差序列存在单位根。

3 实证分析

本文对2005年我国汇率制度改革以来，我国人民币对美元汇率波动和中美利差之间的关系进行贝叶斯平滑转移协整关系的探究。实证中，根据金中夏等[19]的观点，选择2005年8月到2013年7月的人民币对美元月汇率平均值、我国金融机构隔夜拆借利率月加权平均值和联邦基金利率月平均值作为原始样本。对已有的数据进行以下预处理：本月汇率值与上月汇率值的商作为本月汇率波动；我国金融机构隔夜拆借利率平均值与联邦基金利率月平均值之差作为中美利率利差。

3.1 平滑转移模型选择

首先进行汇率波动与中美利差之间的平滑转移回归的贝叶斯分析，得到模型参数的贝叶斯估计，选择拟合程度高的平滑转移模型。下面先设定模型的几种形式，探讨变量之间的非线性关系的存在性与非线性的形式。

(20)

(21)

(22)

在MH-Gibbs抽样过程中，首先对每个模型中的参数进行60000次抽样，舍弃其前10000次结果，取k=2对剩余序列进行稀释，得到模型参数估计的仿真图。图1～2分别给出了参数的Geweke收敛诊断图和后验概率密度图。

图1 参数的Geweke收敛性诊断图

由图1可知，参数的Geweke统计量的绝对值小于1.96，在95%的置信水平下，可判断迭代初的样本均值与迭代末的样本均值不存在显著差异，抽样获得的Markov链是收敛的。说明MH-Gibss抽样方案的收敛性很好。

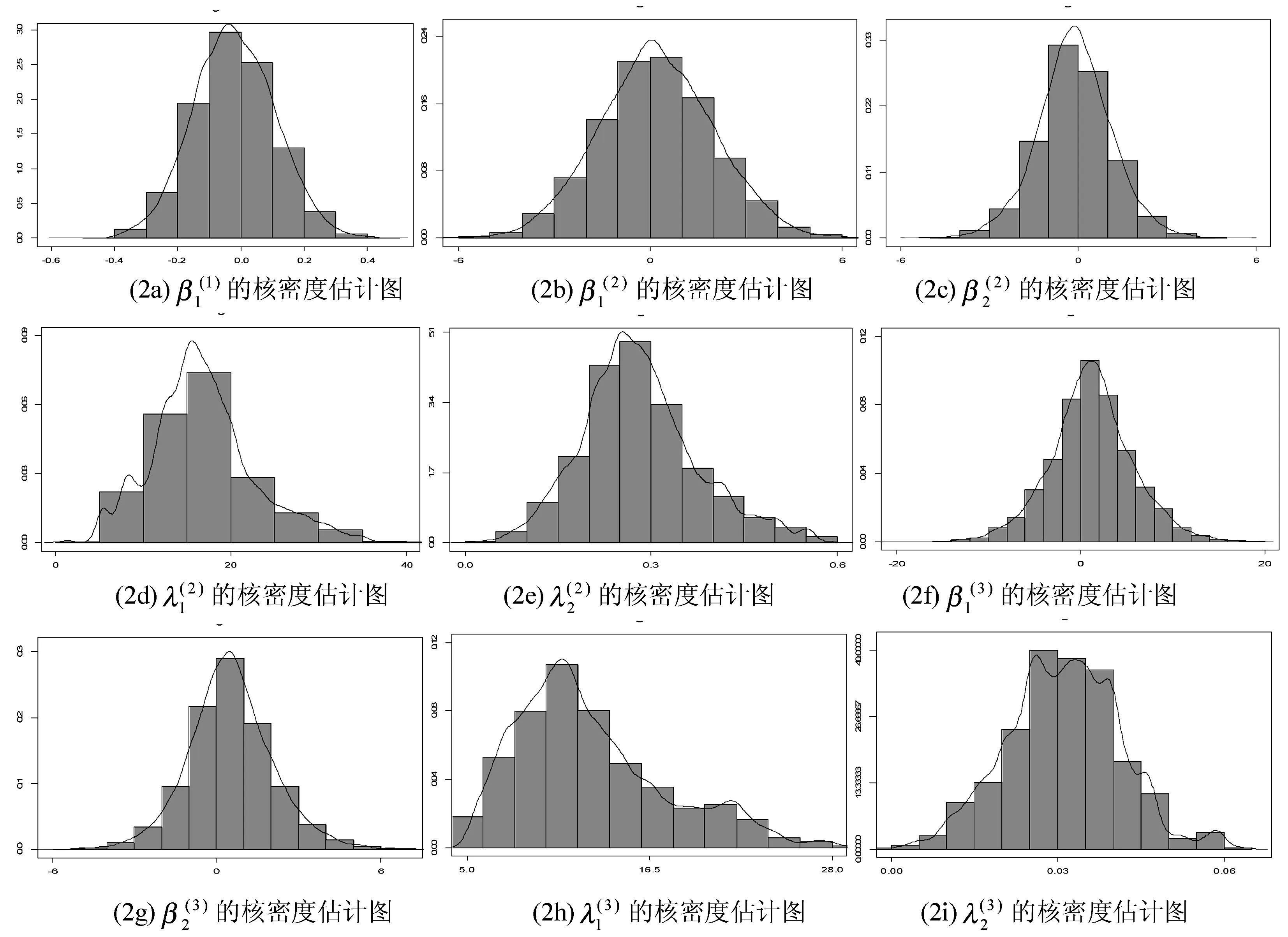
图2 参数后验概率密度图

根据MH-Gibbs抽样结果，利用MCMC数值计算方法可以模拟得出参数的贝叶斯估计值及特性。表1给出了上面三个模型中参数的估计值、标准差、MC误差、2.5%分位数、97.5%分位数以及模型的BIC值。

表1 贝叶斯STR模型的MCMC估计结果

3.2 平滑转移协整分析

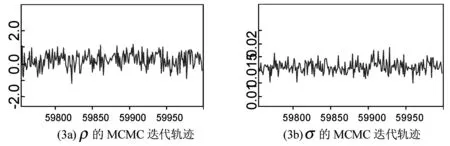
图3 参数的MCMC迭代轨迹

图4 参数的核密度估计图

从图3可以发现，参数的迭代轨迹基本平稳，没有呈现出明显的周期性和规律性；并且参数的自相关系数很快降低到0。从图4可以看出，各参数的概率密度曲线平滑，具有明显的单峰对称特征，表明参数估计的误差较小。这些特征说明抽样方法的有效性，模型各参数的样本分布准确收敛于参数的后验分布，从而保证由此迭代得到的参数估计的准确性。

根据Gibbs抽样结果，结合核密度估计图，可以根据模拟结果得到参数的贝叶斯估计值。表2给出了残差回归模型下参数的均值、标准差、MC误差、2.5%分位数、97.5%分位数及中位数的贝叶斯估计值。

表2 贝叶斯单位根检验模型的参数估计

从表2可以得到以下结论：首先，各参数的MC误差远远小于标准差，证明了Gibbs抽样方法的收敛有效性，其次，对汇率波动与中美利差的平滑转移回归残差进行单位根检验，参数ρ的估计值为0.1806，相应的95%的置信区间为(-0.7324,1.0300)。同时利用(19)式计算贝叶斯因子，得到P(|ρ|≥1)=0.03787, 则K01=25.4061远远大于1，从而也得出了回归残差平稳的结论。两步检验法证明了新汇率制度改革以来，人民币对美元汇率波动与中美利差之间存在非线性协整关系，两者之间存在长期的平滑转移调整机制，我国人民币的市场化趋势明显。

4 结束语

本文利用贝叶斯统计分析方法在平滑转移回归模型基础上对人民币对美元的汇率波动与中美利差数据进行平滑转移协整分析，避免平滑转移回归模型参数估计难以收敛且有偏的问题，简化平滑转移协整检验的算法，从而提高非线性协整检验的精确度和准确度，有助于我国宏观经济政策的正确执行。实证表明：新汇率制度改革以来，人民币兑美元汇率波动与中美利差存在长期的平滑转移协整关系。汇率与利率之间的联动机制得到了深化，在推行货币政策时，应该考虑对当期汇率市场的影响。未来研究可以考虑将更多影响汇率波动的变量引入模型，同时对转移变量进行贝叶斯选择，更好地发现汇率波动的影响因素。

[1] Engle R F, Granger C W J. Co-integration and error correction: representation, estimation, and testing [J]. Econometrica: journal of the Econometric Society, 1987, 55(2): 251-276.

[2] Balke N S, Fomby T B. Threshold cointegration[J]. International economic review, 1997, 38(3): 627- 645.

[3] 王成勇.多机制半参数平滑转换回归模型——兼论我国宏观经济运行周期[J].数理统计与管理,2012，31(1)：96-104.

[4] 王相宁,李文.基于SVAR模型的汇率影响因素分析[J].运筹与管理，2010，19(2)：134-139.

[5] Granger C W J, Terasvirta T. Modelling nonlinear economic relationships[M]. New York: Oxford University Press, 1993.

[6] EitrheimØ，Teräsvirta T. Testing the adequacy of smooth transition autoregressive models[J]. Journal of Econometrics, 1996, 74(1): 59-75.

[7] Choi I, Saikkonen P. Testing linearity in cointegrating smooth transition regressions[J]. The Econometrics Journal, 2004, 7(2): 341-365.

[8] Kapetanios G, Shin Y, Snell A. Testing for cointegration in nonlinear smooth transition error correction models[J]. Econometric Theory, 2006, 22(2): 279-303.

[9] Serra T, Zilberman D, Gil J M, et al. Nonlinearities in the US corn-ethanol-oil-gasoline price system[J]. Agricultural Economics, 2011, 42(1): 35- 45.

[10] 彭方平，胡新明，展凯.通胀预期与央行货币政策有效性[J].中国管理科学，2012，20(1)：1-7.

[11] Ben Cheikh N. Non-linearities in exchange rate pass-through: evidence from smooth transition models[J]. Economics Bulletin, 2012, 32(3): 2530-2545.

[12] Béreau S, Villavicencio A L, Mignon V. Nonlinear adjustment of the real exchange rate towards its equilibrium value: a panel smooth transition error correction modelling[J]. Economic Modelling, 2010, 27(1): 404- 416.

[13] Wang J C, Holan S H. Bayesian multi-regime smooth transition regression with ordered categorical variables[J]. Computational Statistics & Data Analysis, 2012, 56(12): 4165- 4179.

[14] Gefang D. Money‐output Causality revisited-a bayesian logistic smooth transition VECM perspective[J]. Oxford Bulletin of Economics and Statistics, 2012, 74(1): 131-151.

[15] Lopes H F, Salazar E. Bayesian model uncertainty in smooth transition autoregressions[J]. Journal of Time Series Analysis, 2006, 27(1): 99-117.

[16] Chib S, Greenberg E. Understanding the metropolis-hastings algorithm[J]. The American Statistician, 1995, 49(4): 327-335.

[17] Koop G. An objective bayesian analysis of common stochastic trends in international stock prices and exchange rates[J]. Journal of Empirical Finance, 1994, 1(3): 343-364.

[18] Meligkotsidou L, Tzavalis E, Vrontos I D. A bayesian analysis of uinit roots and structural breaks in the level, trend, and error variance of autoregressive models of economic series[J]. Econometric Reviews, 2011, 30(2): 208-249.

[19] 金中夏,陈浩.利率平价理论在中国的实现形式[J].金融研究，2012,(7):63-74.

Nonlinear Cointegration Analysis of Exchange Rate Based on Bayesian Smooth Transition Regression Model

ZHU Hui-ming1, ZHOU Feng1, ZENG Zhao-fa2, LI Rong1, YOU Wan-hai1

(1.CollegeofBusinessAdministration,HunanUniversity,Changsha410082,China; 2.CollegeofFinanceandStatistics,HunanUniversity,Changsha410082,China)

In the method of testing smooth transition cointegration, estimating parameters are uncertain and the problem of cointegration test is complex. This paper proposes a smooth transition regression model and conducts a Bayesian nonlinear cointegration analysis. Based on the selection of parameters prior of the model and the characteristics of the posterior conditional distributions of the parameters, Metropolis-Hasting within Gibbs sampling algorithm is designed to estimate the parameters and bayesian unit root test is utilized to test the stationarity of regression residual, addressing the uncertainty of parameters estimation and the complexity of cointegration test. At the same time, the research applies exchange rate of RMB against U.S. dollar and interest rate differential between China and U.S. to conduct an empirical analysis. The research outcome indicates that MH-Gibbs can effectively a estimate the parameters of the smooth transition model, and we find there is smooth transition cointegration relationship between exchange rate fluctuation and interest rate differential.

transition regression model; nonlinear cointegration; Bayesian analysis; MH-gibbs sampling; exchange rate fluctuation

2013-10- 02

国家自然科学基金创新研究群体项目(71221001)；国家自然科学基金资助项目(71171075，71031004)

朱慧明(1966-)，男，湖南湘潭人，教授、博士生导师，研究方向：贝叶斯计量经济模型；周峰(1991-)，女，硕士研究生，研究方向：金融工程与风险管理。

F831.5，O212.8

A

1007-3221(2015)04- 0225- 08