Origin在共振法测量固体材料的杨氏模量实验数据处理中的应用
2015-07-03余潇杭张军朋
余潇杭,张军朋
(华南师范大学,广东广州 510006)
杨氏模量反映固体材料抵抗外力产生拉伸(或压缩)形变的能力,根据动力学共振法原理,采用悬挂法来测量固体材料的杨氏模量能准确反映材料在微小形变时的物理性能,测得值精确稳定,对脆性材料也能测量,该方法被广泛使用[1-3]。
实验中求杨氏模量需要测出样品的固有频率,然而本实验无法直接测出,而是采用外延测量法测量基频共振频率来代替样品固有频率。这就需要先用已测出的数据绘制曲线,再按照曲线规律延长到求值范围,在延长线部分求出所要的值。这就对作图以及求延长线部分极值点的精确度提出更高要求。传统的手工作图和人主观确定极值点难免造成较大的误差,采用Origin软件的多项拟合(Fit Polynomial)、微分(Differentiate)和由X(Y)值求Y(X)值(find X(Y)from Y(X))功能,参考李艳琴等人《动力学共振法测量固体杨氏模量》一文中的实验数据[4],介绍一种用 Origin对该实验数据进行处理的方法,操作简单,精确直观。
1 实验原理
对于一长为L的细棒,如图1,棒的轴线沿x方向,那么棒在z方向的振动(棒的横振动)满足动力学方程式中η为棒上距左端x处横截面在z方向的位移,E为该棒的杨氏模量(单位为Pa),ρ为材料的密度,S为棒的横截面积,I为棒的某一截面对棒的中心轴线(x轴)的惯性矩[5]。
对于直径为d的圆棒,惯性矩I为:

根据特定的边界条件定出常数K,代入横截面的惯性矩I,就可以得到具体条件下的关系式,结合方程(1)的通解,可得到超越方程:cosKLchKL=1,其根依次是:

只要长度L确定,Kn就可以确定。第一个根“0”对应于静止状态,第二个根KnL=4.730 0,与此对应的振动频率为基频(固有频率)。从试样棒做基频振动波形图,即图2,可以看出,试样棒在作基频振动时存在两个节点,它们的位置距离端面0.224 L(距离另一端面为0.776 L)处。
将KnL=4.730 0代入式子(3),结合圆的面积公式,得到对于直接为d的圆棒,其杨氏模量为
其中,f1为圆棒的基频频率。

图1 棒的横振动
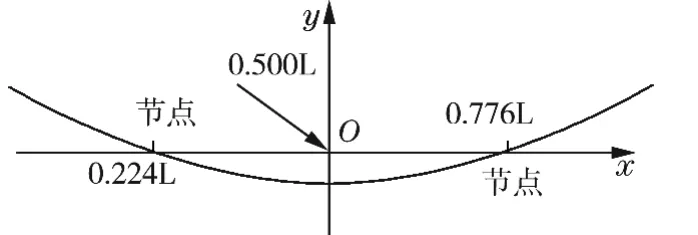
图2 基频振动波形图
由于式(5)在试样的直径与长度之比趋于零时才能满足,因此对试样的不同径长比作出修正,即
T1为修正系数,修正系数是由径长比确定的,如表 1 所示[6]。

表1 径长比与修正系数的关系
由于本实验的试样机械品质因数Q较大,最小约为 50,根据,两者相差较小,可以测量共振频率代替基频频率(固有频率)。
实验中,若要测量试样棒的基频频率,只能将悬线挂于0.224 L和0.776 L节点处,但该节点处的振动幅度几乎为零,很难激振和检测,故采用外延法测基频共振频率。即本实验采用测量棒上几个不同位置的共振频率,根据已测数据绘制曲线,将曲线按照原来规律延长,找到曲线最低点(即结点)所对应的频率,即为棒的固有频率f1。
2 实验数据处理
用Origin软件的多项拟合(Fit Polynomial)、微分(Differentiate)和由X(Y)值求Y(X)值(Find X(Y)from Y(X))功能对实验数据进行处理。
2.1 实验数据
本实验使用的仪器是SG-9动态型杨氏模量测试仪,示波器等。通过调节信号源频率,观察示波器上的电信号波形,测出悬线位于不同位置的共振频率f1,本文采用李艳琴等人《动力学共振法测量固体杨氏模量》一文中对于黄铜横棒测量到的实验数据进行处理,如表3所示,以此为例介绍Origin软件在该实验数据处理中的应用。

表2 悬线位于试样棒不同位置测到的共振频率
2.2 实验数据处理
第一步,数据输入。Origin启动后会自动生成一个工作表Worksheet,将表3的数据输入表格Data1中,其中悬线位置x(mm)数据置于x(X)列中,共振频率f(Hz)数据置于f(Y)列中,如图3所示。
第二步,绘制f-x散点图。选中Data1中的x(X)列和f(Y)列,然后点击菜单中的Plot中Symbol中的Scatter键,得到f-x散点图,如图3所示。
第三步,多项拟合f-x曲线。选中Graph1,点击菜单Analysis中Fitting中的Fit Polynomial(多项拟合)键,弹出选项对话框,勾选Polynomial Order为6次,即进行6次项拟合,并选择Find Specific X/Y中 Find Y from X,点击“OK”,得到 f-x曲线以及相关系数R值,如图4,R=0.998 83,说明拟合效果很好。同时,在Book1中还会生成一个表格Fit Polynomial Find Y from X,只要在该表格中“Enter x values”列中输入需要的 x值,“Y value”列就会自动输出该拟合好曲线上该x值对应的点的y值。该步骤是为了方便在接下来找到最低点坐标对应的x值之后,将x值输入该表格就可以找到最低点的y值,即材料的基频频率f1。
第四步,对频率-位置函数f(x)求微分。根据第三步,要知道曲线f-x最低点纵坐标,首先要确定最低点横坐标,即求曲线f-x的极小值点。在数学上,求一条曲线的极值点,即找到该曲线函数的导函数值为0的点,该点的横坐标即为曲线上最低点的横坐标。基于以上的方法,现在对频率-位置函数f(x)求微分。

图3 原始数据及f-x散点图
选中实验数据,点击Analysis中的Differentiate健,在弹出的对话框中勾选 Plot Derivative Curve项,即输出微分曲线,点击“OK”,得到微分数据表和微分曲线,如图5。
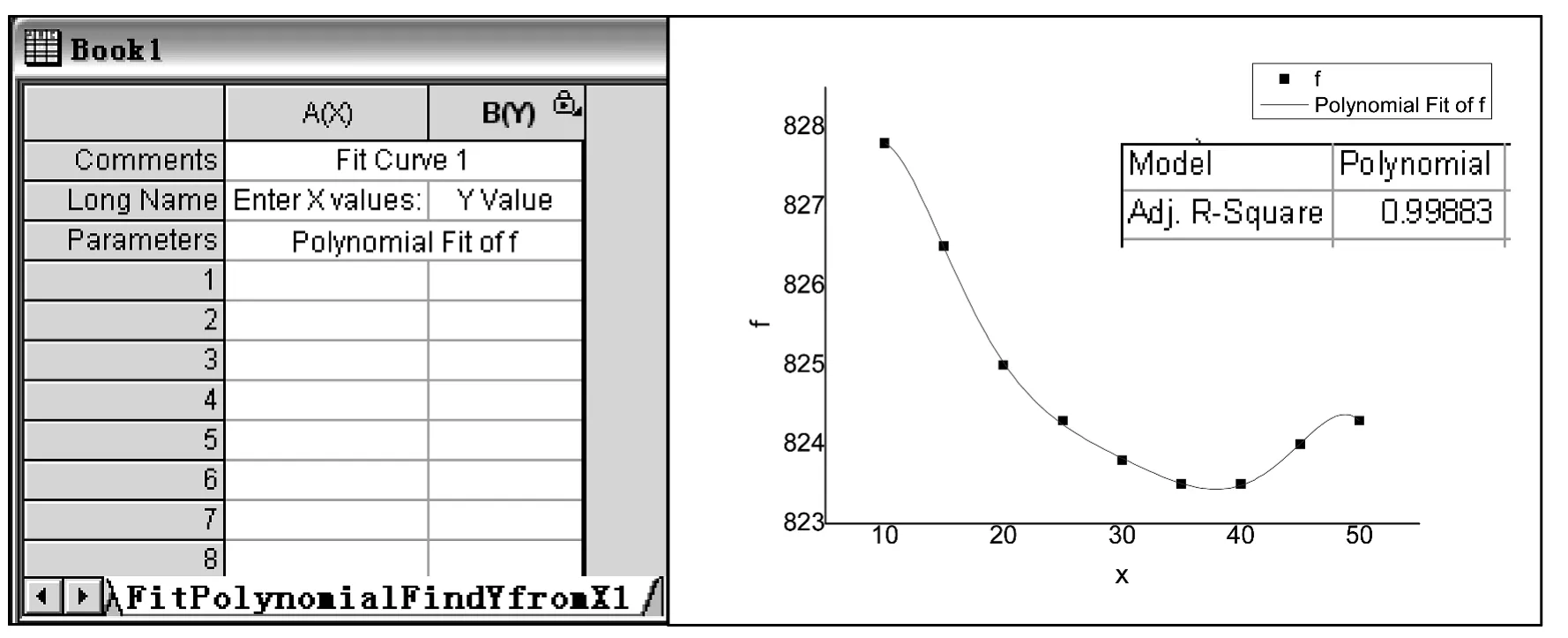
图4 “Find Y from X”输入框及f-x曲线

图5 微分数据表和微分曲线
第五步,多项拟合微分曲线。由于第四步得到的微分曲线并不是圆滑曲线,因此要拟合微分曲线。按照第三步的方法,采用多项拟合,勾选Polynomial Order为6次,并选择Find Specific X/Y 中 Find X from Y,点击“OK”,得到“Find X from Y”输入框及f-x微分曲线和其相关系数R值,如图6所示,相关系数R=0.985 69,拟合效果较好。同时,在Book1中还会生成一个表格Fit Polynomial Find X from Y1,只要在输入框中输入y值,就能得到f-x微分曲线上该y值对应的点的横坐标x。
第六步,求导函数值为0的点横坐标。在图6中所示“Find X from Y”输入框的“Enter Y values”列中输入0,则在“X value”列就会自动输出f-x微分曲线上y值为0的点对应的横坐标,输出结果为x=36.752 43,如图7所示。

图6 “Find Y from X”输入框及f-x微分曲线
第七步,求 f-x曲线的极小值点。将 x=36.752 43输入图4中所示“Find Y from X”输入框,即在“Enter X values”列中输入 36.752 43,则在“Y value”列就会自动输出f-x曲线上x值为36.752 43的点对应的纵坐标,输出结果为 y=823.445 7,如图7所示。也就是基频共振频率为f1=823.445 7 Hz。
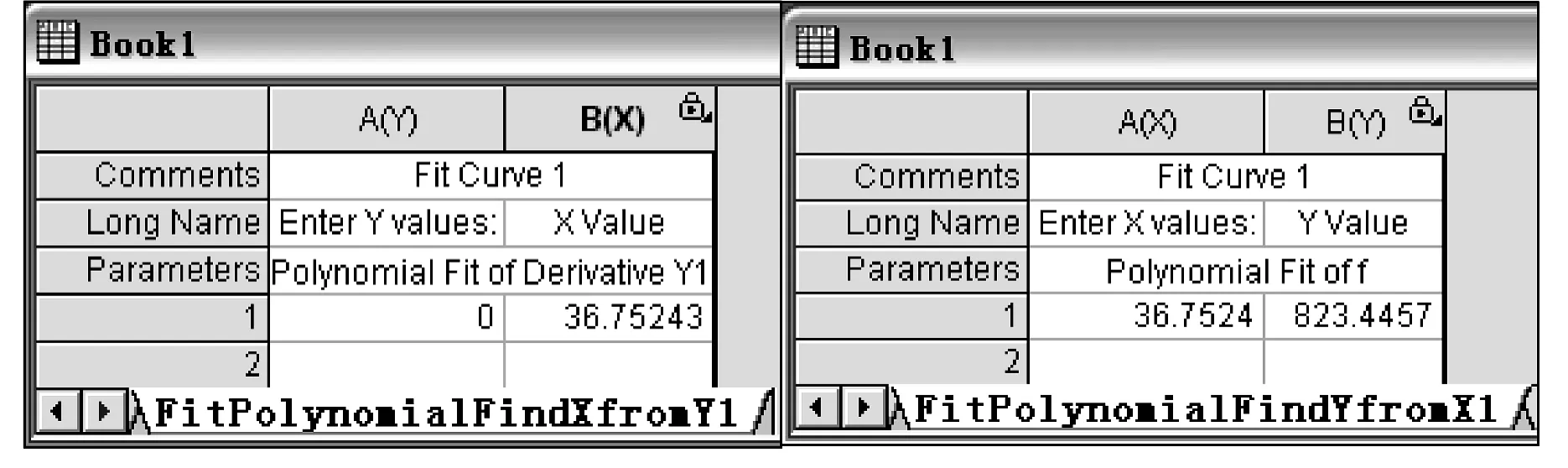
图7 “Find Y from X”输入框及“Find Y from X”输入框
2.3 实验结果
根据以上数据处理的结果,被测材料黄铜棒的基频共振频率为f1=823.445 7 Hz,结合测到的棒的长度平均值 L=166.78 mm,直径 d=7.937 mm,质量m=69.6 g,通过查表1,修正系数为 T1=1.014,代入式(6),得到黄铜的杨氏模量为E=8.99 ×1010Pa。
理论推导得到试样棒的基频振动理论节点位置为0.224 L[7-9],即本实验的理论值为 x0=37.4 mm,而本文用Origin处理实验数据,得到的节点位置x=36.752 43 mm。比较实验值和理论值,计算百说明用该方法处理实验数据得到的结果接近理论值,误差可能由于仪器的精度造成。
3 结 论
采用Origin软件的多项拟合(Fit Polynomial)、微分(Differentiate)和由 X(Y)值求 Y(X)值(find X(Y)from Y(X))功能,对共振法测量固体材料的杨氏模量实验数据进行处理,操作简单,精确直观。
此外,该方法还可以拓展运用到用Origin软件求曲线极值点,相比于传统手工作图,人为取最低点的主观性,这种方法比较精确方便。
综上所述,将Origin软件引入物理实验数据处理中,有利于提高实验结果的精确度,也有利于提高实验数据处理的效率。
[1] 黄亦明.动态法测定材料的杨氏模量[J].物理与工程,2002,12(5):35-36.
[2] 赵星晨,李雪梅,夏雪琴.Metlab软件和送差法在拉伸法测量杨氏模量中的应用[J].大学物理实验,2014(4):110-112.
[3] 唐振坤,张登玉.Origin软件在用霍尔传感器测量杨氏模量实验中的应用[J].大学物理实验,2013(6):61-63.
[4] 李艳琴,赵红艳,李学慧,胡瑞.动力学共振法测量固体杨氏模量[J].实验室研究与探索,2009,28(10):17-19.
[5] 李学慧.大学物理实验[M].北京:高等教育出版社,2005:187-196.
[6] 余观夏,张爱珍,阮锡根.用共振法测定动态杨氏模量实验装置的改进[J].物理实验,2004,24(2):41-46.
[7] 方利广.大学物理实验[M].上海:同济大学出版社,2006:209-213.
[8] 张建伟.Origin 9.0科技绘图与数据分析超级学习手册[M].北京:人民邮电出版社,2014:251,294.
[9] John.R.Taylor.An introduction to error analysis——the study of uncertainties in physical measurements[M].Sausalito,California:University Science Books.1982.
