冲击加速度校准中低通滤波器的应用

贾秋燕，盛侃

(中航工业北京长城计量测试技术研究所，北京100095)

冲击加速度校准中低通滤波器的应用

贾秋燕，盛侃

(中航工业北京长城计量测试技术研究所，北京100095)

介绍了在冲击加速度校准中，为了抑制电、机械等干扰和噪声对冲击加速度测量结果的影响，采用二阶巴特沃斯型低通滤波器，通过时间序列翻转、二次滤波等方式，实现零相移的低通滤波效果。并比较不同截止频率下，低通滤波器对衰减程度不同的冲击加速度波形产生的峰值偏差，给出不同加速度波形下，低通滤波器截止频率选择应注意的问题。

冲击加速度;低通滤波;零相移

0 引言

冲击加速度校准过程中，会受到各种各样的高频干扰，包括电干扰和机械干扰。这些高频干扰信号叠加在冲击加速度信号上，会影响对加速度峰值的判断。因此有必要对采集到的冲击加速度信号进行低通滤波，滤除高频干扰信号。采用的低通滤波器包括硬件和软件两种实现方式。硬件滤波通常由加速度传感器后端的信号调理器实现，软件滤波则是针对采集后的加速度数字信号，通过软件编程实现。冲击加速度运动是具有明确起点和终点的非周期过程，冲击加速度运动在时域表现为典型的脉冲过程，在频域则表现为具有无限带宽的连续频谱［1］，任何方式的低通滤波都会对加速度波形造成不同程度的衰减。因此如何选择低通滤波的截止频率、阶数以及低通滤波器应用后对加速度峰值的影响，是值得关注的问题。本文将对冲击加速度校准中低通滤波器的应用进行分析。

1 低通滤波器的类型

冲击加速度校准中需要使用低通滤波器滤除机械的、电的干扰和噪声、谐振等。GB/T20485.13－2007《振动与冲击传感器校准方法第13部分:激光干涉法冲击绝对校准》中对低通滤波器的要求为:“能够抑制高频噪声而不使信号发生畸变”。由于冲击脉冲频域上连续的特性，理想的低通滤波器应具有通带内幅频特性平坦，相频特性为线性的频率响应，能够保证滤波后信号不会产生失真。常用的低通滤波器类型有切比雪夫、贝塞尔、巴特沃斯。其中切比雪夫滤波器虽然幅频特性在通带内较为平坦，但相频特性远离线性;贝塞尔滤波器相频特性具有很好的线性，但幅频特性单调下降，不够平坦;巴特沃斯滤波器则在通带内具有最平坦的幅频特性，相频特性也较为线性。GB/ T20485.13－2007推荐使用的是四阶巴特沃斯低通滤波器。这种滤波器相频特性较为线性，但仍然会因为相位偏移导致失真。为了获得更好的相频特性，GB/T20485.13－2007还推荐利用零相移技术设计零相位偏移的巴特沃斯型低通滤波器。原理是先使数字信号序列正向通过滤波器，然后将输出序列在时间轴上翻转，再通过同样的滤波器进行二次滤波，最后将二次滤波后序列再进行时域翻转，即可实现零相位。零相移巴特沃斯型的低通滤器原理图如图1所示。

图1 零相移滤波器原理图

图1中，X(z)是输入信号z变换;H(z)是一个巴特沃斯低通滤波器传递函数的z变换;Y(z)是输出信号z变换。Y(z)为

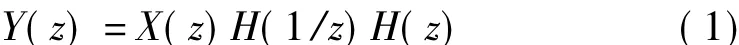
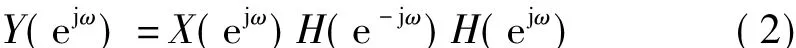
由于H(z)为实系数式，因此H(e－jω)=H*(ejω)，H*(ejω)是H(ejω)的复共轭，则

输入数字信号序列频谱的幅度被频率响应函数修改，而相位无变化，实现了零相移滤波［2］。在零相移滤波器中进行二次滤波，多采用二阶的巴特沃斯型低通滤波器。二阶的巴特沃斯滤波器的传递函数如式(4)。

式中:ωn为自然角频率。频率响应见图2。

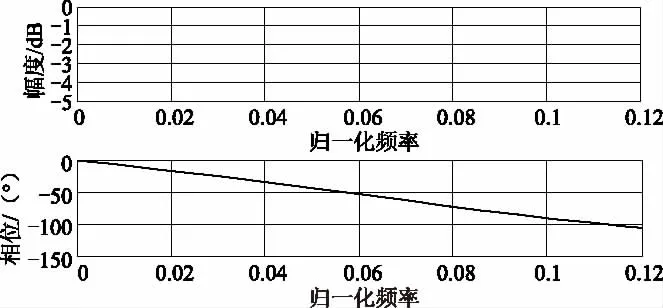
图2 二阶的巴特沃斯型低通滤波器幅频和相频特性

2 低通滤波器截止频率的影响

本文选用一个标准冲击加速度波形和与其加速度峰值和脉冲持续时间相近的两组实测冲击加速度波形，三组波形采样率和点数相同，经过零相移巴特沃斯型低通数字滤波器对其进行滤波，截止频率分别为10/T，9/T，8/T，7/T，6/T，5/T，4/T，3/T，2/T，1/T(T为冲击加速度持续时间，单位为秒)，比较因低通滤波器引入的冲击加速度峰值测量偏差。为了防止由于冲击加速度波形的不平滑及峰值判读方法影响本文的比较结果，本文尽量选用较为平滑的冲击加速度波形，峰值判读方法统一为冲击加速度波形的最大值。

2.1 标准半正弦脉冲

以加速度峰值ap为100g(1g=9.81 m/s2)、持续时间T为0.01 s的标准半正弦冲击加速度脉冲为例，时域图形见图3，频谱见图4。

图3 标准半正弦冲击加速度脉冲时域波形

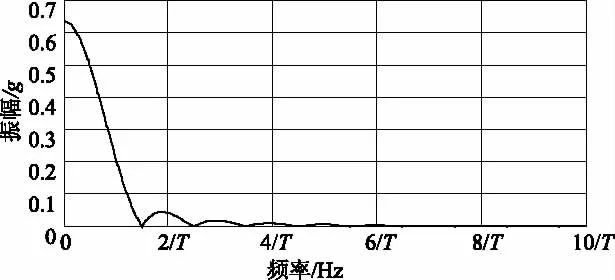
图4 标准半正弦冲击加速度脉冲频谱

本文采用零相移巴特沃斯型低通数字滤波器进行滤波，当截止频率从10/T逐渐降低到1/T时，其输出信号的峰值偏差如表1所示。

表1 峰值偏差(标准半正弦冲击加速度脉冲)

从表1可以看到，为了保证峰值偏差在1%以内，低通滤波器的截止频率应选择在2/T以上。但在实际的冲击测量过程中，很难产生理想的半正弦波形，一般冲击激励源所产生的冲击加速度脉冲波形是近似半正弦波形，没有半正弦那么饱满，会出现上升沿和下降沿要比标准半正弦波形陡峭，甚至会向曲线内部凹陷的现象，这样就导致波形在频域上的能量分布向高频部分延伸，能量集中区域的频带要宽于同等量值和持续时间的标准半正弦波形，并且随着滤波器截止频率的降低，加速度峰值测量误差增大。

2.2 实际冲击加速度脉冲

本文选用两组冲击加速度峰值和脉冲持续时间相近但变化率不同的实测冲击加速度脉冲来进行比较。

加速度峰值为109.32 g，脉冲持续时间为0.0104 s的实测冲击加速度波形见图5中的波形1，频谱见图6中的波形1。

当采用零相移巴特沃斯型低通数字滤波器进行滤波、截止频率从10/T逐渐降低到1/T时，其输出波形的峰值偏差如表2所示。

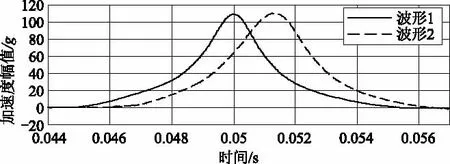
图5 时域波形的比较

图6 频谱的比较

加速度峰值为110.44 g，脉冲持续时间为0.0105 s的实测冲击加速度波形见图5中的波形2，其频谱见图6中的波形2。

当采用零相移巴特沃斯型低通数字滤波器进行滤波、截止频率从10/T逐渐降低到1/T时，其输出波形的峰值偏差如表3所示。

表2 峰值偏差

表3 峰值偏差

由两组实测加速度时域波形可看到:波形1在加速度峰值附近的收腰现象较波形2更为严重，即波形1中的高频分量较为丰富;两组波形在加速度上升沿和下降沿处的陡峭程度存在差异。表4给出了不同加速度幅值处波形的上升沿下降沿时间间隔。

表4 不同加速度幅值处两个波形的对应时间间隔

由图5、图6可知，两组实测冲击波形的时域加速度峰值非常接近，但随着冲击加速度峰值的增加，波形1的脉冲持续时间较波形2衰减更为迅速。在频域上表现为:波形2的主峰值明显高于波形1的主峰值，在低频段，波形1的幅值低于波形2的幅值;在高频段，波形1的幅值高于波形2的幅值。两组波形在时域和频域的差异，导致相同截止频率的低通滤波器引入的峰值偏差不同。随着低通滤波器截止频率的降低，波形1的冲击加速度峰值偏差高于波形2的冲击加速度峰值偏差。同理，实测冲击波形与理想冲击波形，在时域上理想冲击波形较实测冲击波形更为饱满;在频域中，则表现为实测冲击波形中高频分量在整个波形频谱中所占的比重高于理想冲击波形。因此相同截止频率的低通滤波器，对实测冲击波形产生的影响更为严重，表现为实测冲击波形加速度峰值偏差高于理想冲击波形。综上所述，进行冲击校准时，必须考虑低通滤波器引入的冲击加速度峰值的测量误差。

3 结论

采用经典半正弦激励脉冲的实验室冲击校准中，一般规定低通滤波器的截止频率不小于10/T，从上述的分析中可以看出，低通滤波引入的峰值偏差能够控制在1%以内;当机械、电干扰较为严重时，可适当将低通滤波器的截止频率缩小至5/T，低通滤波引入的峰值偏差能够控制在5%以内。针对收腰现象极为明显的加速度波形，在降低截止频率之前，应比较一下不同截止频率所带来的加速度峰值偏差，在允许的误差范围内选择合适的截止频率。

［1］国防科工委科技与质量司.力学计量［M］.北京:原子能出版社，2002.

［2］徐磊，陈淑珍，肖柏勋.一种新的零相移数字滤波器的改进算法［J］.计算机应用研究，2005(4):21－22.

Analysis of the Low Pass Filter’s Application in Shock Acceleration Calibration

JIA Qiuyan，SHENG Kan
(Changcheng Institute of Metrology＆Measurement，Beijing 100095，China)

This paper introduces the realization of low pass filter effect of zero phase shift in shock acceleration calibration by means of a two－order Butterworth low pass filter，time series of turnover and two filteringmodes，in order to restrain the influence of electrical，mechanical and other interference and noises on the measurement results of shock acceleration.We compared the peak deviation on the shock acceleration waves of different attenuation degreeswith the low pass filter at different cut－off frequencies，and proposed the issues thatare noticeable in selecting cutoff frequencies of the low pass filter with different acceleration wave forms.

shock acceleration;low pass filter;zero phase shift

TB93

A

1674－5795(2015)01－0030－03

10.11823/j.issn.1674－5795.2015.01.07

2014－11－03;

2014－12－02

贾秋燕(1972－)，女，工程师，从事测试计量技术研究及仪器仪表推广方面的工作。