有关电磁波横向多普勒效应的辨析

曹春梅

（华北电力大学数理系，河北 保定 071003）

当波源和探测器相对运动时，探测器探测到的波频率与源本身频率不等的现象称为多普勒效应.对电磁波，多普勒效应通常分为纵向多普勒效应和横向多普勒效应.当电磁波源和探测器沿二者连线方向运动时，探测器探测到的源辐射频率与静止源的辐射频率不等的现象称为纵向多普勒效应；当电磁波源或探测器垂直于电磁波矢方向运动时，探测器探测到的源辐射频率与静止源的辐射频率不等的现象称为横向多普勒效应[1].对电磁波的纵向多普勒效应，电动力学教科书中多有讨论，易于理解且无争议，但对于电磁波的横向多普勒效应，多数文献只是泛泛一提，并未针对具体情况进行相应的分析和讨论，也有文献虽然进行了较具体的讨论，但给出横向多普勒效应的频移既有红移，又有蓝移的结论[2，3].本文基于光行差公式，对电磁波的多普勒效应红移和蓝移进行了全面的辨析，并针对横向多普勒效应的两种具体情况进行了讨论，指出电磁波的横向多普勒效应仅有红移，不应存在蓝移，分析了文献[2]、[3]给出的横向多普勒效应蓝移错误结论的原因.

1 电磁波的多普勒效应

当电磁波源和探测器都相对于介质系运动时，探测器测得的波的频率ωd与波源的频率ωs之间的关系称为普遍的多普勒效应公式[2]，如下式所示

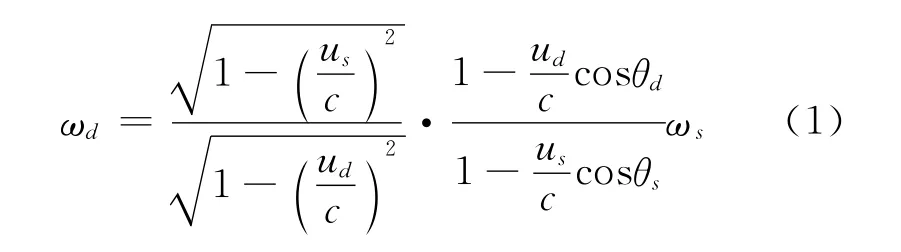
式中，us和ud分别为波源和探测器相对于介质系的运动速率，θs为在介质系中波源速度us与波矢k之间的夹角，θd为在介质系中探测器速度ud与波矢k之间的夹角.

当探测器相对于介质系静止时，ud等于零，式（1）的结果为

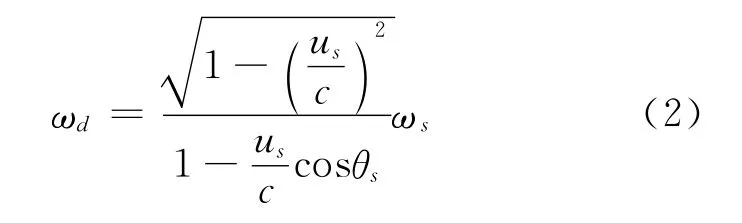
与文献[1]、[4]给出的光波多普勒效应数学表达式相同.

2 电磁波的纵向多普勒效应

（1）如果波源和探测器均相对于介质系运动，且沿二者连线相互接近，则θs＝0，θd＝π，代入式（1）中有

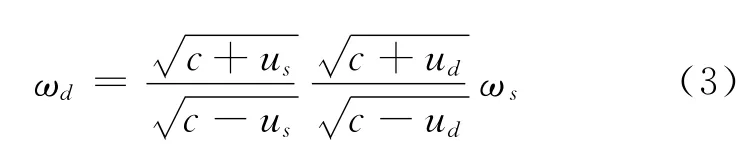
此时若波源运动，探测器静止，即us≠0，ud＝0，则；若波源静止，探测器运动，即us＝0，ud≠0，则

（2）如果波源和探测器均相对于介质系运动，且沿二者连线相互远离，则θs＝π，θd＝0，代入式（1）中有

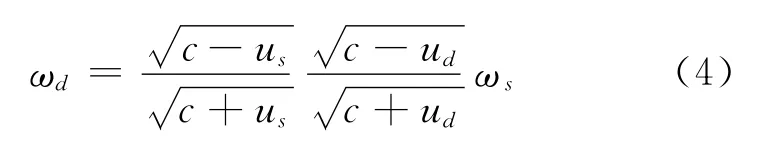
此时若波源运动，探测器静止，即us≠0，ud＝0，则若波源静止，探测器运动，即us＝0，ud≠0，则

由（3）、（4）两式可知，当源的运动或探测器的运动与波矢方向平行时，若二者相互接近，探测器探测到的频率大于源的频率，为多普勒效应蓝移[4]；若二者相互远离，探测器探测到的频率小于源的频率为多普勒效应红移[5].此即电磁波的纵向多普勒效应，纵向多普勒效应既有红移也有蓝移，且波源的运动与探测器的运动总是等价的.

3 横向多普勒效应红移

众所周知，光的方向就是注视物体时看到物体的方向，因此横向多普勒效应应当是从探测器观察波矢时，波源沿与波矢垂直的方向运动，或探测器沿与波矢垂直的方向运动，即以探测器为参照系时给出波源速度与波矢之间或探测器速度与波矢之间夹角的取值总为时所得出的结论.据此进行以下两种情况下的分析：

（1）若探测器相对于介质系静止，即探测器与介质系合二为一，则ud＝0，若探测器观测到波源沿与波矢垂直的方向运动，则代入式（1），从而有

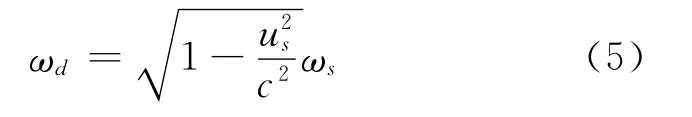
式中，ωd为探测器探测的结果，说明此时发生了横向多普勒效应，且探测到的频率小于源本身的频率，即发生了横向多普勒效应红移.

（2）若波源相对于介质系静止，即波源与介质系合二为一，则us＝0.若探测器探测到其运动方向与波矢的运动方向垂直，意味着以探测器为参考系时探测器速度与波矢之间夹角的取值为但这并不代表介质系中探测器运动方向与波矢方向之间的夹角也为二者之间存在光行差（即运动中的观测者所观测到的波源视方向与静止的观测者所观测到波源的真方向之差）.根据光行差公式[6]，两个惯性系S和S′对两个方向之间夹角的测量结果并不相同，二者之间有如下关系

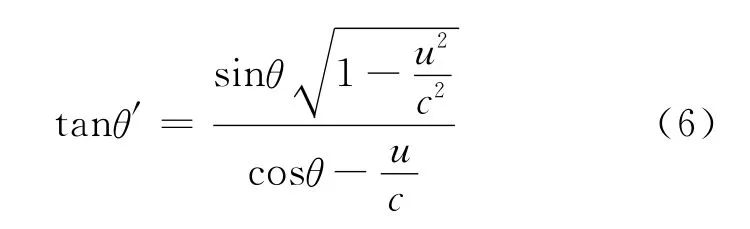
式中，θ为S系测得的两个方向之间的夹角，θ′为相对于S系运动的S′系测得的两个方向之间的夹角，u为S′系相对于S系的运动速度.显然若探测器参考系中探测器速度与波矢之间夹角θ′＝根据式（6），则介质参考系中必有

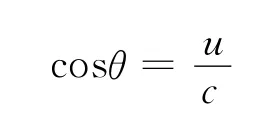
探测器相对于介质系的速率为，则代入式（1），有

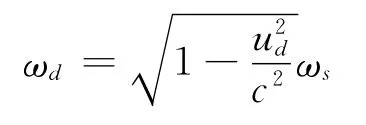
式中，ωd为探测器探测的结果，说明此时发生了横向多普勒效应，且探测到的频率小于源本身的频率，即亦发生了横向多普勒效应红移.

由以上分析可知，无论是探测器相对于介质系静止、波源相对于介质系运动，还是波源相对于介质系静止、探测器相对于介质系运动，电磁波的横向多普勒效应总是红移，由此也说明对于电磁波的横向多普勒效应，波源的运动与探测器的运动是等价的.

4 横向多普勒效应蓝移错误结论的原因分析

对横向多普勒效应，文献[2]中给出了探测器相对于介质系静止，波源沿与波矢垂直的方向运动时，探测器接收到的光波的频率ωd与光源的频率ωs之间的关系为（红移），而当光源相对于介质系静止，探测器沿与波矢垂直的方向运动时，探测器接收到的光波的频率ωd与光源的频率ωs之间的关系为（蓝移）.文献[3]中给出了接收器静止，波源作圆周运动时接收器上的钟所测得的周期与光源上的钟所测得的周期之间的关系为（红移），而当波源静止，接收器作圆周运动时接收器上的钟所测得的周期与光源上的钟所测得的周期之间的关系为（蓝移）.由此可见，在文献[2]、[3]中，接收器静止、波源运动和接收器运动、波源静止的横向多普勒效应分别出现了红移、蓝移两种不同的结果，显然与狭义相对论中波源的运动与探测器的运动等价相矛盾，其根本原因在于电磁波横向多普勒效应中蓝移的结论是错误的.下面以文献[2]为例分析其横向多普勒效应蓝移错误结论的原因.

文献[2]认为当光源相对于介质系静止，即光源与介质系合二为一，则us＝0，若观测到探测器沿与波矢垂直的方向运动，则将其值代入式（1）中，即为文献[2]给出的结论，但这一结论是错误的，错在没有分析“探测器沿与波矢垂直的方向运动”这句话的物理含义，没有正确理解式（1）中θd所在参照系，而是将θd简单地取为直接代入式（1）中，因而得出了“横向多普勒效应蓝移”的错误结论.实际上无论是“波源沿与波矢垂直的方向运动”还是“探测器沿与波矢垂直的方向运动”总是指探测器测得的结果，即以探测器为参照系时，波源速度us与波矢之间夹角为或探测器速度ud与波矢之间夹角为而式（1）中的θs、θd分别为在“介质系”中观测到的光源速度us与波矢k之间的夹角和探测器速度ud与波矢k之间的夹角.如果探测器相对于介质系静止，波源相对于介质系运动，探测器探测到“波源沿与波矢垂直的方向运动”，等同于介质系中“波源沿与波矢垂直的方向运动”，所以代入公式（1）中得到了横向多普勒效应红移的正确结果.但如果探测器相对于介质系运动，波源相对于介质系静止，“探测器沿与波矢垂直的方向运动”是指探测器认为自己的运动方向与波矢垂直，根据光行差公式，介质系则认为“探测器的运动方向与波矢方向并不垂直，其夹角θd应满足cosθd＝将代入式 （1）中，有ωd＝，即仍然是横向多普勒效应红移.

文献[3]提出的在实验室参照系中，源静止、接收器作圆周运动得出的横向多普勒效应蓝移结果的错误原因及其分析同上.

由以上分析可见，将探测器探测到的波源运动方向与波矢方向的夹角按照光行差公式，转换到介质系中二者之间的夹角θd是正确解决问题的关键，实际上这一点同样适用于纵向多普勒效应，只不过在纵向多普勒效应情况下，探测器探测的角度与介质系测出的角度总相等而已.如当波源和探测器均相对于介质系运动，且沿二者连线相互接近时，如探测器探测到波源运动方向与波矢方向的夹角和探测器运动方向与波矢方向的夹角分别为θ′s＝0，＝π，根据光行差公式，不难得出介质系中波源运动方向与波矢方向的夹角和探测器运动方向与波矢方向的夹角分别为θ′s＝0，＝π；而当波源和探测器均相对于介质系运动，且沿二者连线相互远离时，如探测器探测到波源运动方向与波矢方向的夹角和探测器运动方向与波矢方向的夹角分别为θ′s＝π，＝0，根据光行差公式，不难得出介质系中波源运动方向与波矢方向的夹角和探测器运动方向与波矢方向的夹角为θ′s＝π，＝0.显然与前述纵向多普勒效应的结果相同.

[1]郭硕鸿.电动力学[M].北京：高等教育出版社，1997.

[2]路峻岭，汪荣宝.多普勒效应公式的简便推导[J].大学物理，2005，24（8）：25-27.

[3]高炳坤，王凤林.相对论多普勒效应的简易推导[J].大学物理，2003，22（8）：15-16.

[4]苏景顺，范红.光波多普勒效应的简单证明[J].物理与工程，2008，18（3）：11-12.

[5]别业广.电磁波的多普勒效应[J].物理与工程，2003，13（4）：62.

[6]瑞斯尼克.相对论和早期量子论中的基本概念[M].上海师范大学物理系，译.上海：上海科学技术出版社，1978.