关于一道光学习题的分析与思考

王 瑶

（郑州大学物理工程学院，河南 郑州 450001）

在赵凯华和钟锡华先生编著的《光学》教程中，几何光学部分有这样一道习题：

光线射入如图1所示的棱镜，经两次折射和反射后射出.（图中画出了棱镜的某一截面，简称为棱镜，后文中皆用此约定——作者注.）

（1）证明偏向角与入射方向无关，恒等于2α；

（2）在此情况下，能否产生色散？

注：棱镜内实际光线的交点为O；

入射光线与出射光线的延长线交点为O′；

两次折射法线的交点为O″.

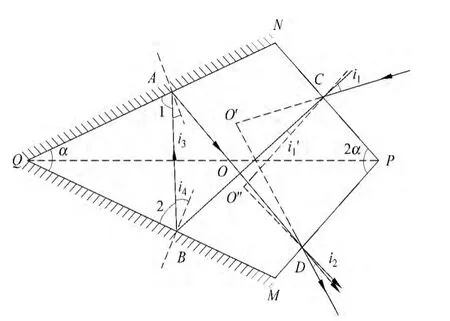
图1

1 问题解答

（1）在此，提供与钟锡华先生等编著的《光学·习题思考题解答》中不同的另一种较为简便的解题方法（∠O″DO＝）：

如图1所示，易知α＝π-∠1-∠2＝i3＋i4，故在△AOB中，∠AOB＝π-2α，即∠COD＝π-2α，⇒∠OCP＋∠ODP＝π.

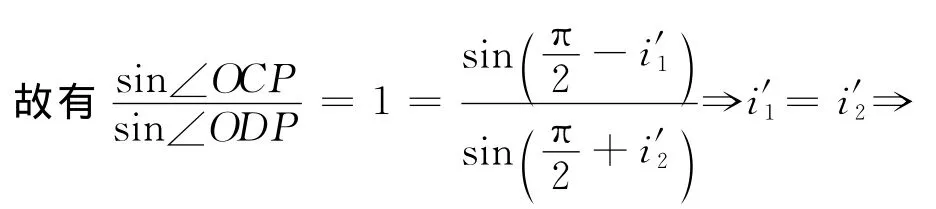
∠O′CO″＝ ∠O′DO″

因此，∠CO′D＝π-2α，即偏向角δ≡2α，与入射角方向无关，且由i′1＝，可得到i1＝i2.

＊在《光学·习题思考题解答》中，关于这道题目的作图是有误的.∠COD，∠CO′D，∠CO″D大小都为π-2α，故图1中，O，O′及O″应在C，D，P三点所确定的圆上.如图1所示，若线段OC在其法线上方，则线段OD也必然在其法线上方，才能保证∠COD大小为π-2α.

（2）由于任何波长的光线出射方向都相同，因此不能发生色散.在此，作为补充，进行另外一些分析.

①光线由C点垂直入射时，光束在棱镜内的光路关于PQ对称.

证明如下：

如图2所示，棱镜关于PQ对称，入射点为C，作BC⊥PC；作AD，使其与BC关于PQ对称，连接AB，可知AB⊥PQ，现要证明CB-BAAD为光路，只需证明∠3＝∠4.

在四边形CPMB中，

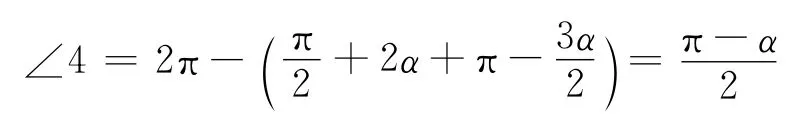
在直角三角形△QEB中

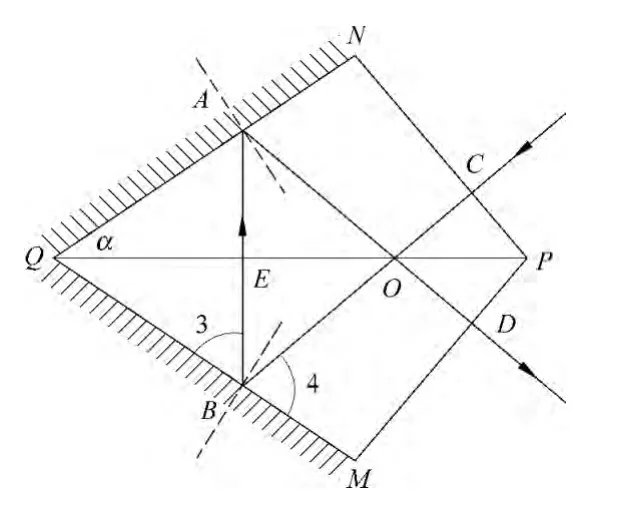
图2

② 光线由C点非垂直入射（图3）

由入射点C依次作关于两次反射界面的对称点，得到其虚像C″，如图3所示.由此可见，在棱镜内部的反射并不能改变两束光线的夹角.因此，出射点D1，D2不可能重合.（图3中法线方向均由棱镜外指向棱镜内.）

图3

2 对该现象原因的分析

如图4所示，把棱镜的4条边平移到相同的起点，作出入射界面NP在两次反射中的虚像，可得a，b，c，d，e5条线段之间的夹角都为，且线段a关于c的虚像与e平行，e关于b的虚像与d平行.故两次反射使入射界面NP的虚像与NP有2α的夹角，并与MP平行.而两平行的折射界面不改变光线的传播方向，如图5所示.因此，偏折角恒为2α.

事实上，这也是求解此题目的另外一种方法.

3 光线由 PN入射,先后经QM、QN反射,并由 PM出射的条件探究

影响因素的分析

首先猜想几种影响因素：

（1）光在棱镜中的相对折射率n[设其中最大频率光线折射率为n1（即最大折射率），最小折射率为n2]；

（2）入射点C的位置；

（3）入射角大小i；

（4）棱镜形状（α角大小）.

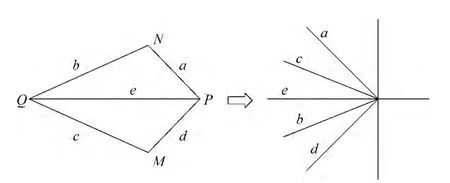
图4

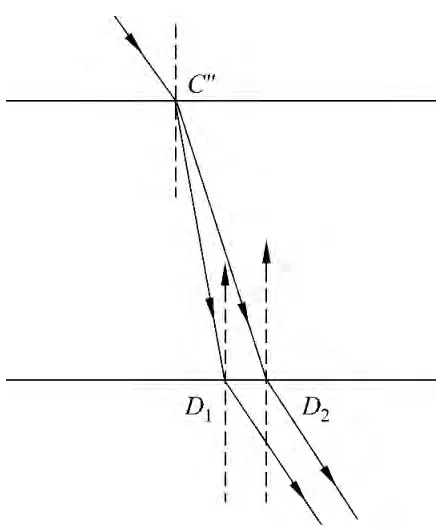
图5

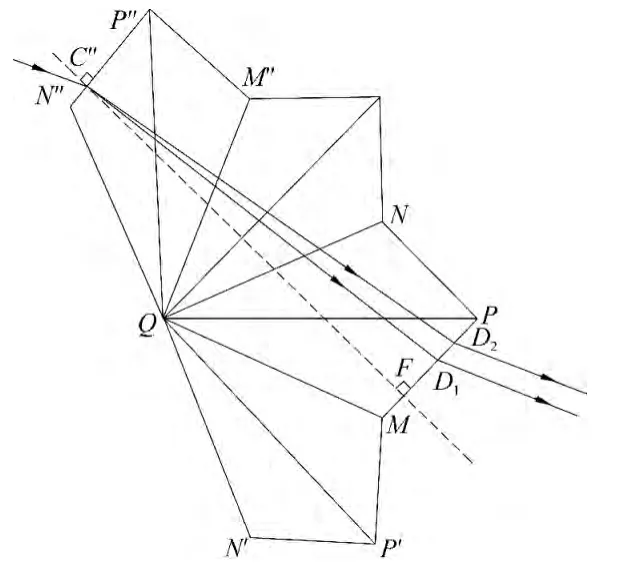
图6

如图6所示，画出整个棱镜先后关于反射界面QM，QN的虚像，N关于QM的对称点为N′，N′，P′，M关于QN的对称点分别为N″，P″，M″.P″N″／／PM.经过虚像C″，光线依次通过QM″，QN到达PM后出射，此即为光线由PN入射，先后经QM，QN反射，并由PM出射的充要条件.

如图6所示，作C″F⊥MP，设P″N″＝PM＝l，C″N″＝l′（0≤l′≤l），光线从界面N″P″法线左侧（对应于图1即法线上方）入射时，入射角i＞0，∠FC″D＞0；光线从该法线右侧（对应于图1即法线下方）入射时，入射角i＜0，∠FC″D＜0.

在 △QN″P″中，由正弦定理可得，QN″＝

在△QN″M中，由正弦定理可得，

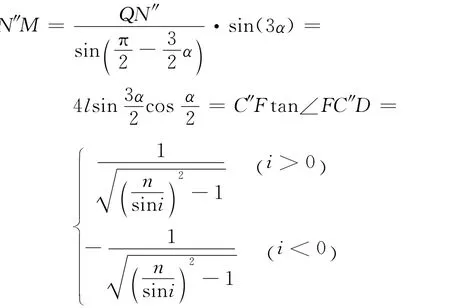
根据α的取值范围划分，可得到表1.

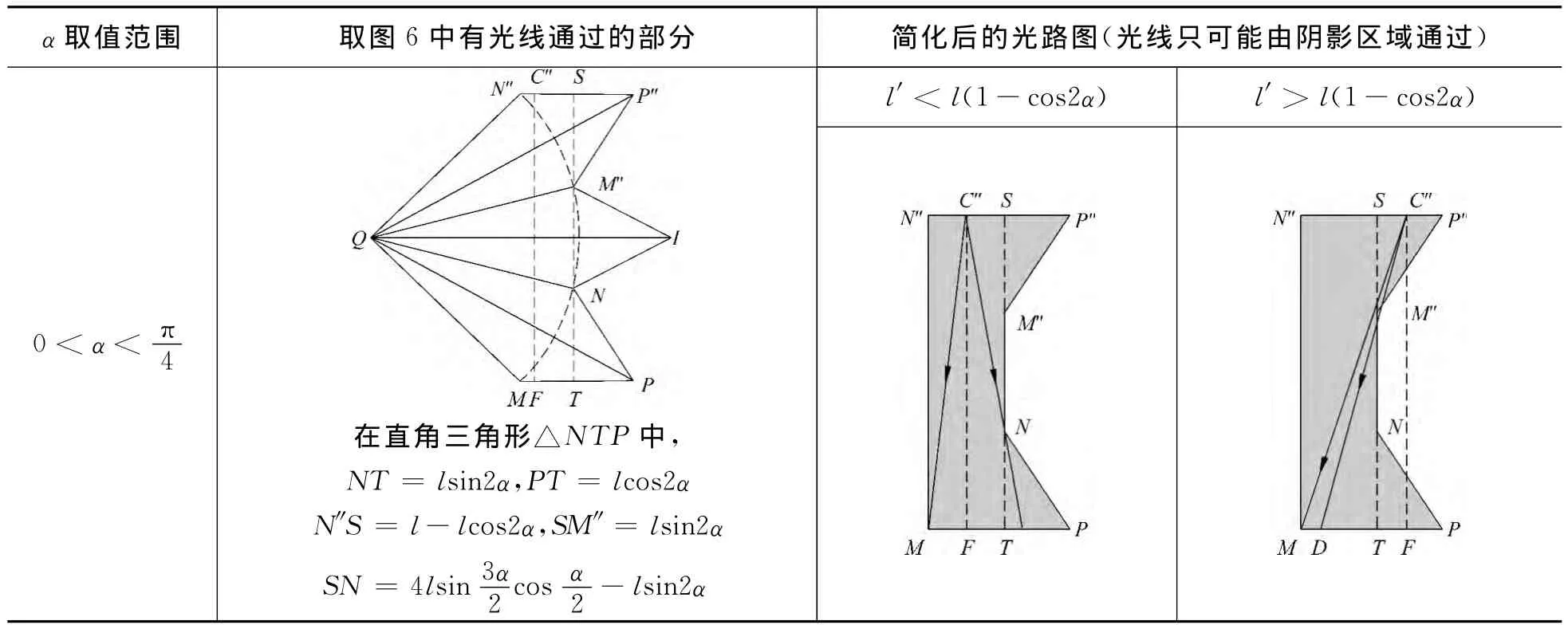
表1 化简光路图

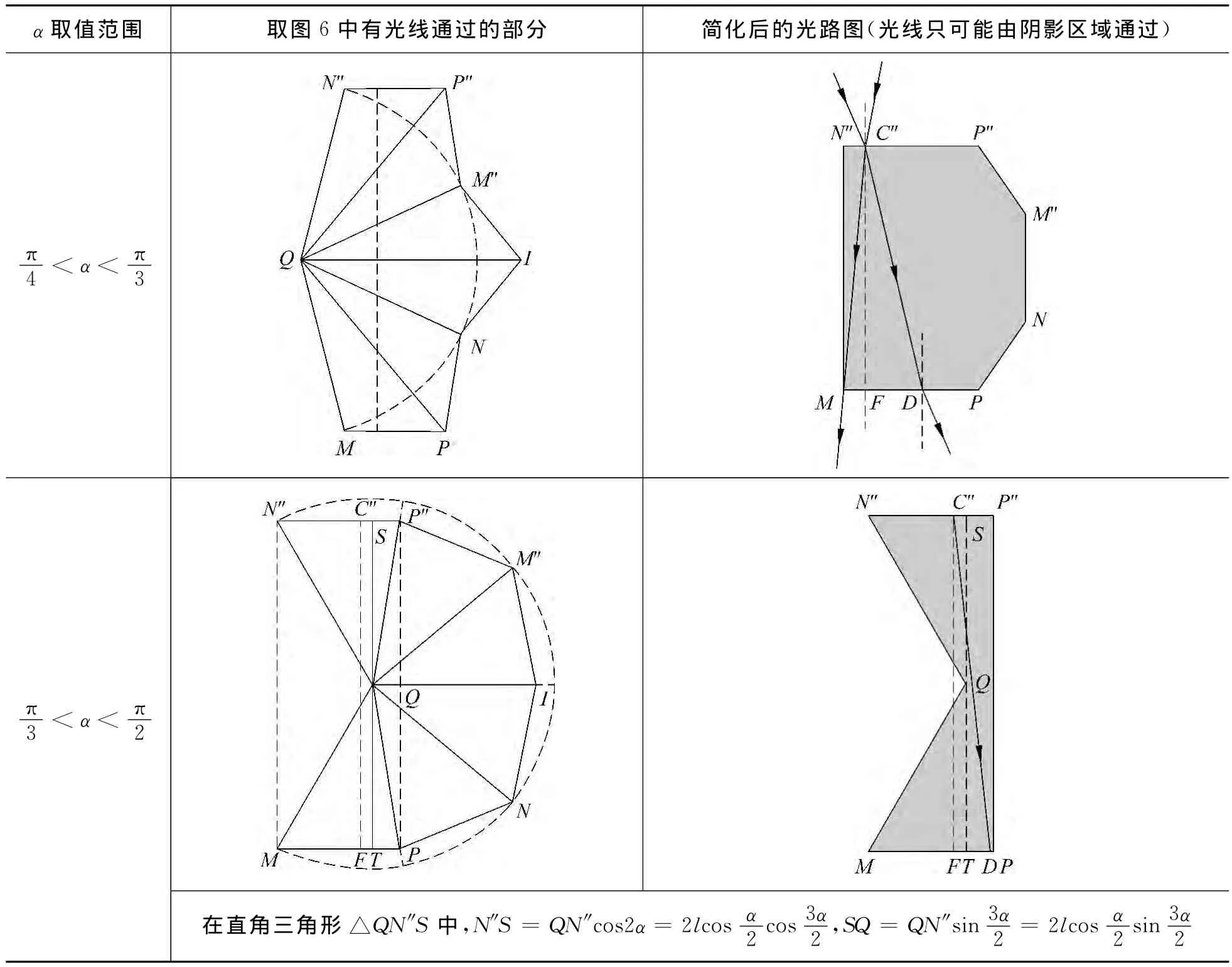
续表

根据α的取值范围，对应于化简后的光路图，容易得出表2的结果.

至此，对于光线由该棱镜PN入射，先后经QM，QN反射，并由PM出射的条件已讨论完毕.

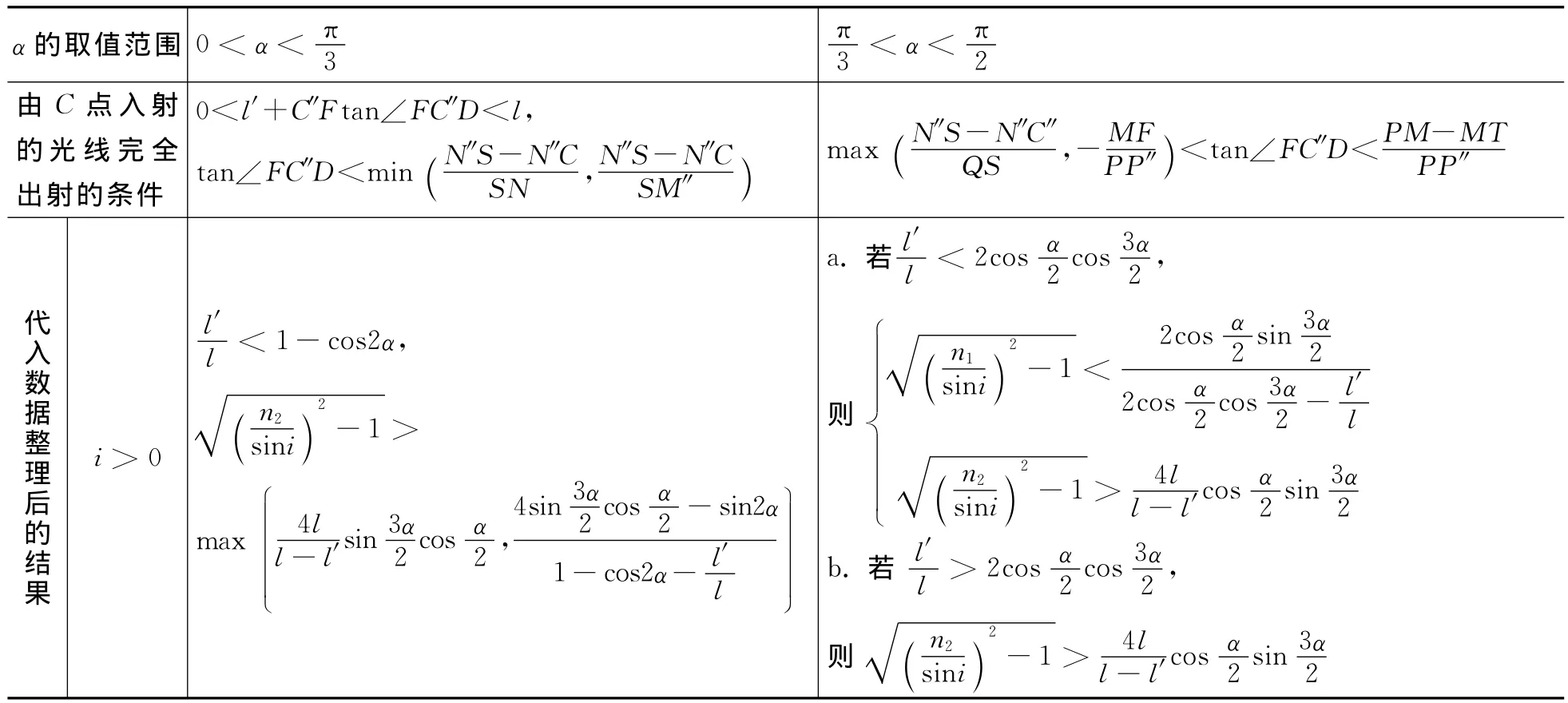
表2 出射条件

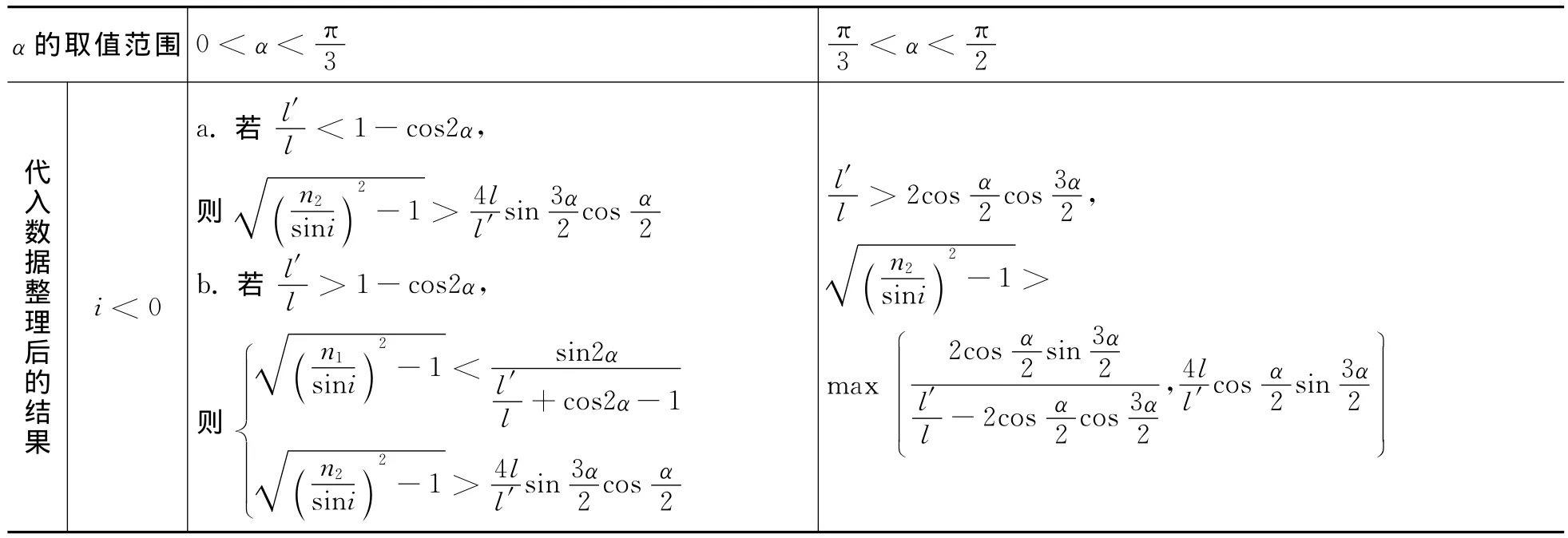
续表

4 分析与讨论

4.1 入射点C的位置

由表1左侧的3幅的光路图可以得到，若0＜α当时，光线须从法线下方入射；若，当时，光线须从法线上方入射，才能先后经QM，QN反射，并由PM射出.

4.2 存在盲区的α临界值

所谓盲区，这里指α值在一定范围内时，入射点在入射界面PN上存在不论i为何值，在界面PM上都无任何出射光线的区域.

4.3 出射光线展宽

若入射光线可由MP界面完全射出，则出射光线展宽为（设D1，D2分别为最大、最小频率光线的出射点）

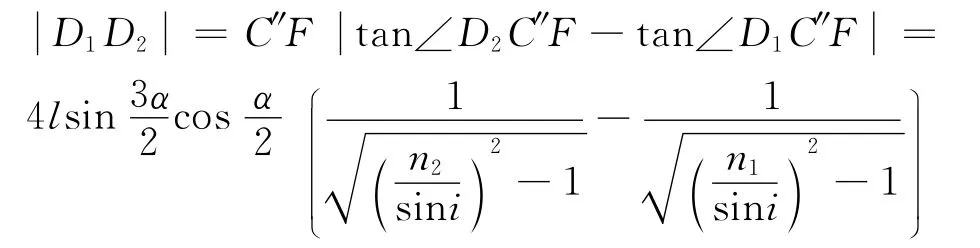
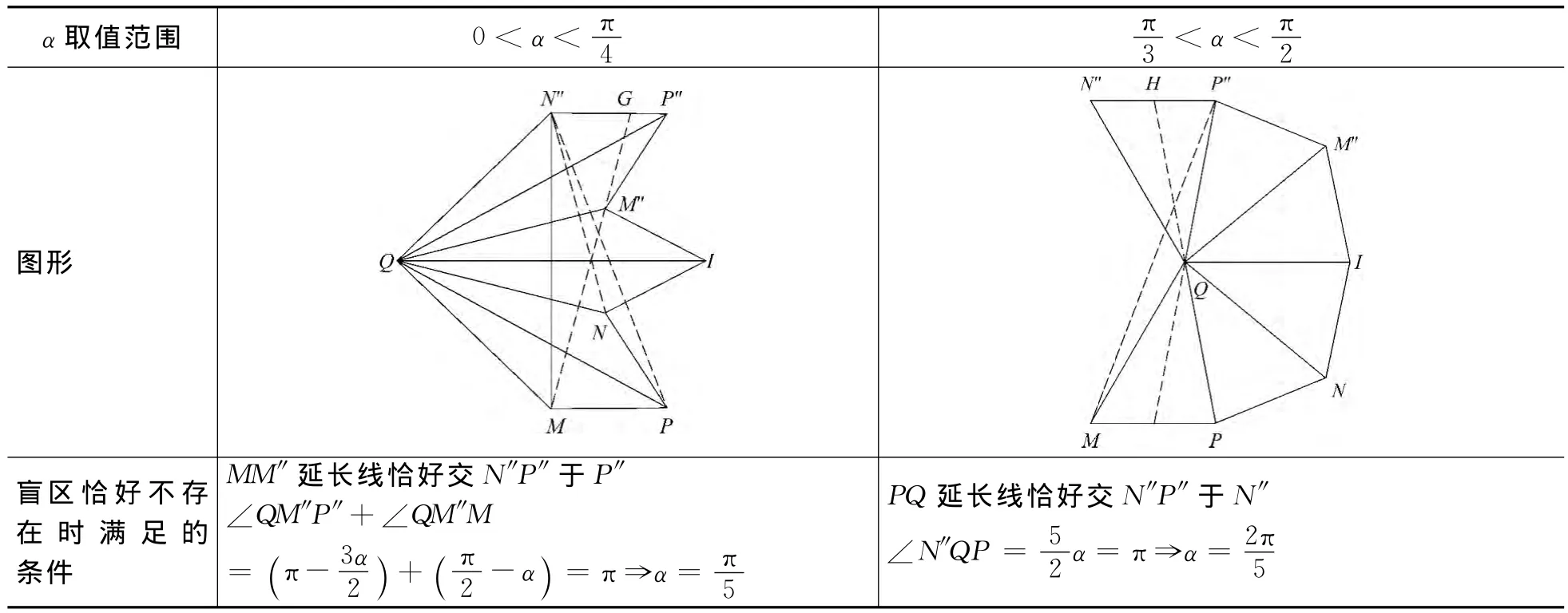
表3 盲区存在分析

[1]赵凯华，钟锡华.光学（上册）[M].北京：北京大学出版社，1984.

[2]钟锡华，骆武刚，邓淑琴.光学习题思考题解答[M].北京：北京大学出版社，2006.