利用迈克耳孙干涉仪测量透明体的折射率

母柏松 马孟祺 陈云琳

（1北京交通大学理学院国家级物理实验中心，北京 100044；2北京交通大学交通运输学院，北京 100044）

迈克耳孙干涉仪是一种典型的分振幅双光束干涉装置，在物理量测量及检测成像等方面有广泛的应用，如：测量钠黄光波长及钠黄光双线的波长差、测量光波的相干长度等[1-3].用迈克耳孙干涉仪测量折射率，一般采用钠光光源，通过观测白光干涉条纹的方法，先调出白光零光程差的彩色干涉条纹，在光路1或2中垂直光线方向插入被测物，再调出零光程差的彩色干涉条纹，反射镜移动距离d与透明体厚度t、透明体折射率n、空气折射率n0（n0大致取关系式（1）[4-7]

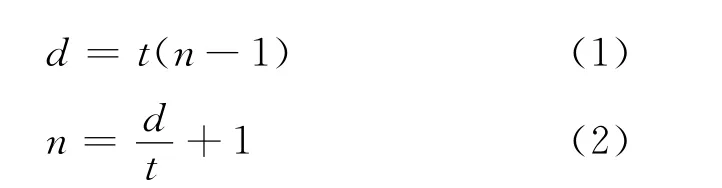
但是该方法必须知道薄透明体的厚度或折射率之一，通过测出M1镜前移的距离d，才能得到测量体的折射率或厚度.本文提出一种使用迈克耳孙干涉仪测量透明体折射率和厚度的新方法，借助单色光的等倾干涉现象，无须已知所测透明体的厚度，通过间接测量，求得透明体折射率和厚度的方法，相比于一般方法，此种方法可以进一步降低系统误差，提高系统精度.

1 实验设计原理

迈克耳孙干涉仪测薄透明体折射率的原理见图1，图1中S为单色光光源，G1和G2是相同的分光板，Q是垂直于光路1方向插入的透明体被测物，Q1是Q经偏转后与光路1成夹角的薄透明体，Q镀银使入射光分为等振幅的反射光1和透射光2，G2起光路补偿作用，M1，M2是平面反射镜，G1，G2与 M1，M2有45°夹角，调整 M1与 M2精确垂直，视场E处可观察到清晰等倾干涉圆环.单色光测薄透明体光程差变化原理见图2，Q与光路1垂直时调出等倾干涉圆环后，在光路以外垂直光路方向使轴缓慢旋转，在E处可观察到等倾干涉圆环吃进或吐出，光程差增加，圆环冒出，反之吃进[4-7]。由图2可知，光程差变化Δ有关系式（3），

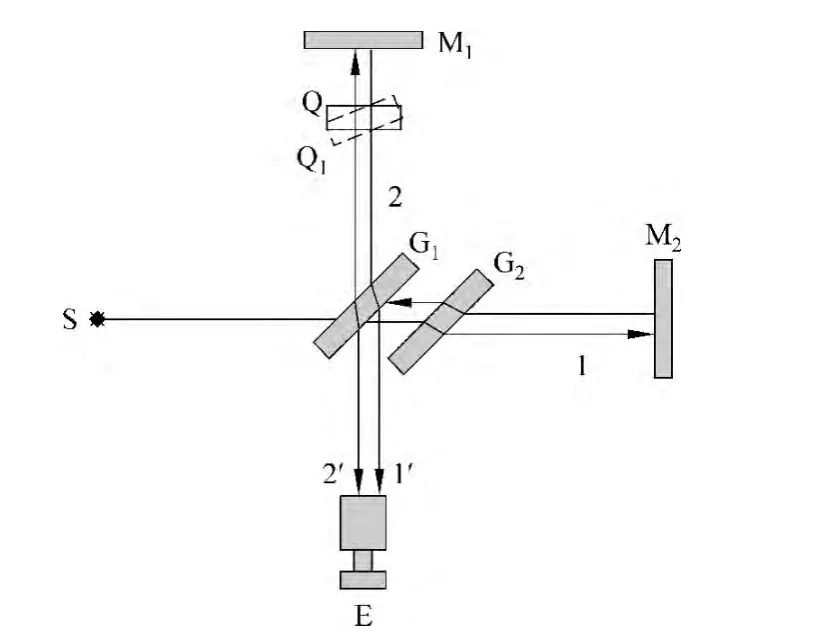
图1 光程差原理图

由图2可知：

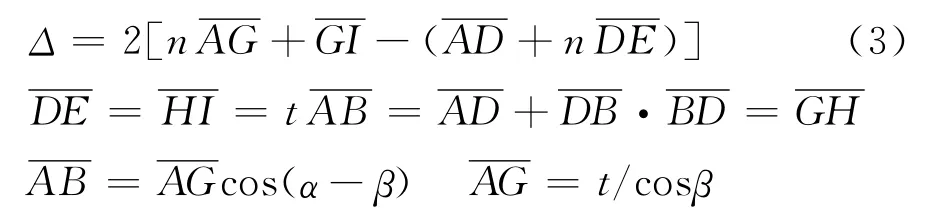
折射定律：n0sinα＝ncosβ（n0＝1）

E处观察到等倾干涉圆环吃进或吐出数N与Δ有：Δ＝Nλ

将Δ代入式（4）得

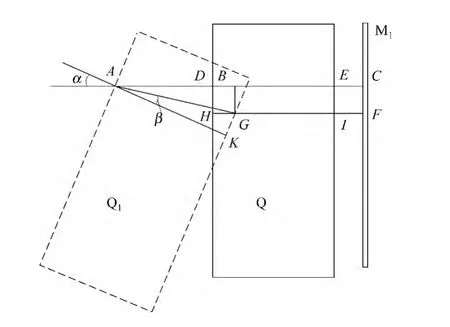
图2 光程差变化原理图

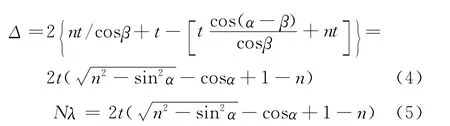
从式（5）可以看出，若测得两组圆环的吞吐数N及相对应的偏转角α，即可求解方程组，求出折射率的大小，进而同时获得透明体厚度的值.

2 透明介质折射率和厚度的测定

选择钠光灯作为单色光源，被测物体选用平板光学分光板，玻璃薄片用自制的固定延伸装置定位在分光计载物台水平方向的中心延长线上，且垂直于载物台，玻璃薄片在水平和垂直方向均可微调.

实验中调整α＝0°时，先调整分光板固定延伸臂α大致等于零，实验中发现在调整α角度过零点时，条纹将发生吞吐变化，吞吐变化拐点处延伸臂与光路1夹角α大致等于零，再微调延伸臂、玻璃薄片，可以观察到薄片反射光形成的等倾干涉圆环，反复调整α角和玻璃薄片使两圆心重合，此时玻璃薄片垂直于光路1，α＝0°，测量时缓慢小心偏转，使分光板沿同一个方向变化.实验装置示意图如图3所示.

α的测量与计算如图4所示，首先使延长臂通过刻度圆盘中心交圆盘于A、B两点记下此两点的读数，然后偏转玻璃薄片，延长臂与刻度圆盘交于C、D两点，记下弧AC，弧CD的度数.在本实验中我们利用自制的钢丝固定延伸装置与分光板相连，通过分光板的转动使得钢丝一起转动，多次读出分光计指示牌上的读数，减少读数误差.根据几何关系有：

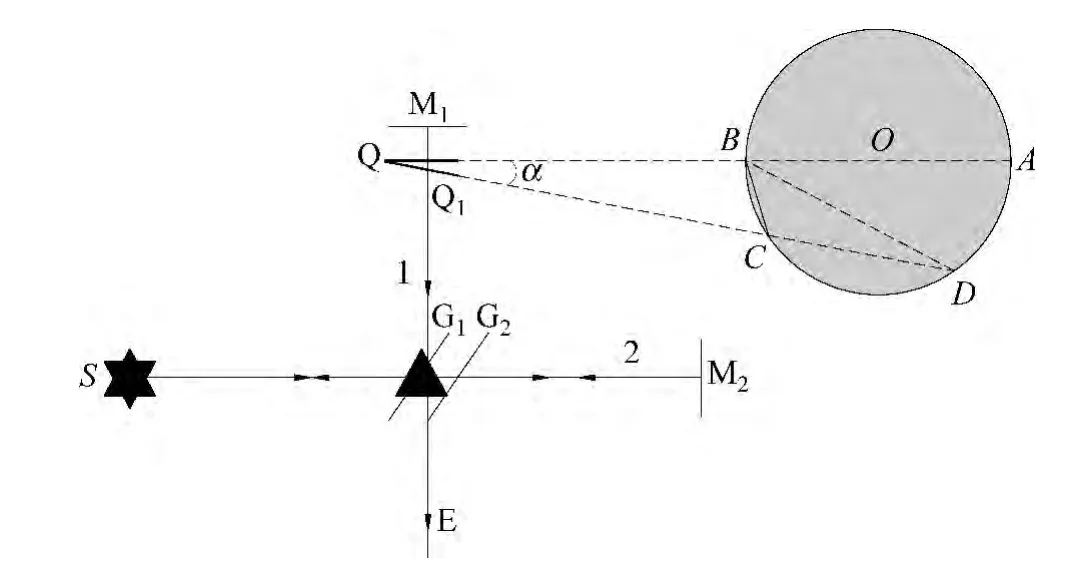
图3 实际装置示意图

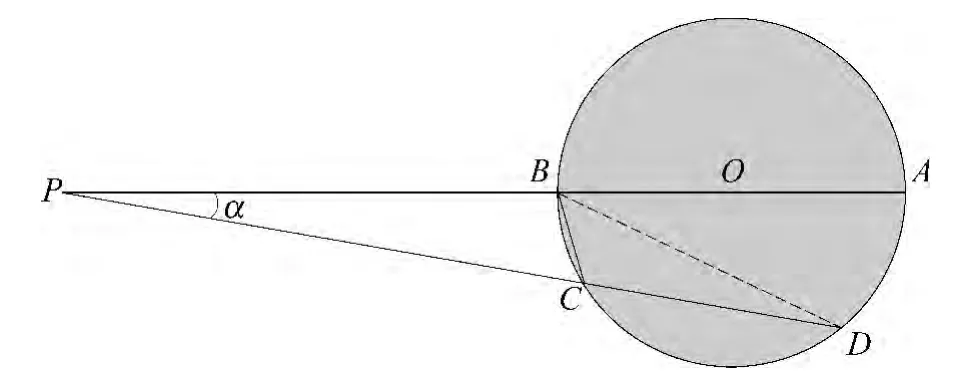
图4 α的测量与计算示意图

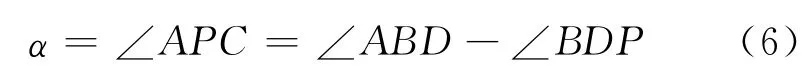
以P为圆心α对应的弧度为

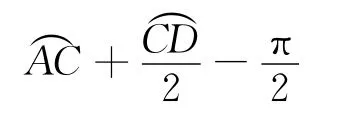
3 理论误差计算

利用上述原理，本实验共测量了8组数据，利用格拉布斯准则剔除了2组坏值，所测得的实验数据见表1，利用测量数据值计算，获得α和n的平均值，由此计算出折射率与厚度的不确定度，具体方法如下：

在本实验中N为吐出圈数，无不确定度，λ＝589.3nm 为常数，故式（5）为间接测量量t，n与直接测量量N，α的关系式，为求得n，t的不确定度，可利用类似于控制变量的方法，分别求解n，t的不确定度，本文提出的方法相当于控制变量法，利用间接测量即可.至于α的不确定度由于人为读数原因会存在绝对误差，但在读数过程中我们采取6次读数求平均值，大大地减少了误差.

首先计算折射率n的不确定度，对于式（5）等号两侧同时对α求导有

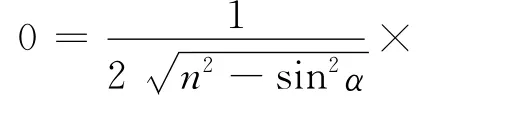
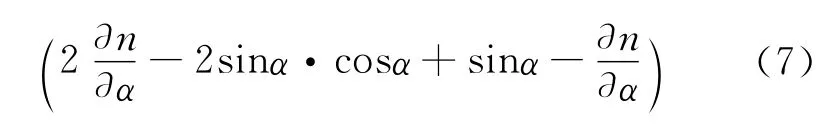
其中n＝1.510，将αi（i＝1，2，3，4，5，6）代入求出不同的值

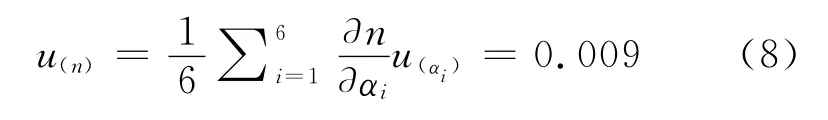
其次计算透明体厚度t的不确定度，同理等号两侧同时对α求导有

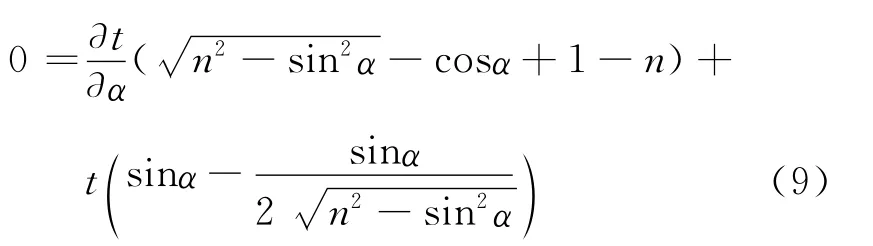
将αi（i＝1，2，3，4，5，6）分别代入式（9）得到值

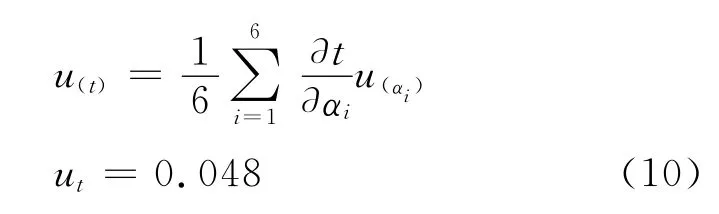
故可得厚度的不确定度为0.048，折射率的不确定度为0.009，故厚度t＝（0.987±0.048）mm，折射率n＝1.510±0.009，与实际给出的厚度t＝（0.990±0.001）mm，折射率n＝1.5216相比较，基本吻合.以上结果表明，在不确定度允许的范围内，玻璃板折射率的实验测量值与真值相符，从而证明了本文所提出的薄透明体折射率与厚度的测量方法是切实可行的.

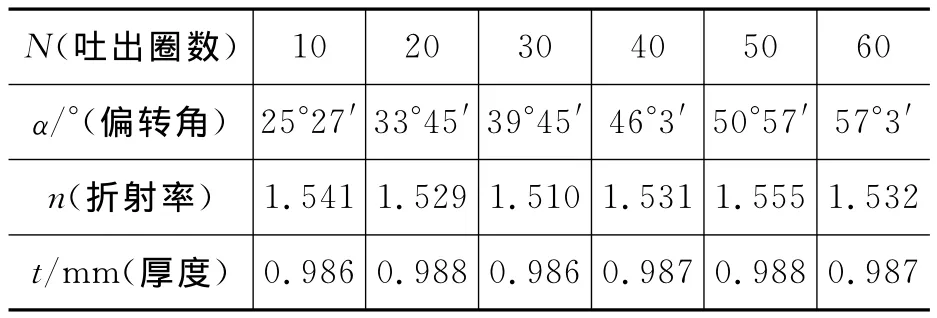
表1 N，α，n，t值记录表

4 结语

实验测量结果表明，本文所提出的实验方法可行，当迈克耳孙干涉仪光路中的被测薄透明体与光路呈不同夹角时，对应的光程变化可通过等倾干涉圆环的变化定量测量出吞吐圆环数、薄透明体厚度、薄透明体折射率、薄透明体与光路夹角之间的关系.本方法测量精度高，使用仪器少，设备简单，影响测量结果的因素少，测试结果与真值吻合较好.实验中只需调整更换被测物，若使用光学减震平台，电子测角仪，并采用计算机处理数据，可进一步提高测量精度，适合实际光测量工程需求.

[1]赵斌.透明体厚度和折射率测量[J].大学物理，2004.23（2）：47-48.

[2]王本菊，张佳慧.光的干涉应用——测量透明介质的折射率[J].中国校外教育（理论），2009（8）：134.

[3]魏茂金，张朝清.迈克耳孙干涉仪测量介质板折射率的问题研究[J].2010，30（6）：28-31.

[4]皇甫国庆.对白光干涉法测量透明介质折射率实验的讨论[J].物理实验，2011，30（7）：28-30.

[5]陶振英.在迈氏仪上用白光干涉测量的方法[J].大学物理，2004，23（2）：47-48.

[6]邓晓颖.迈克耳孙干涉—测薄透明体厚度和折射率[J].西安工业学院学报，2004，24（4）：383-387.