关于水星近日点进动计算的方法
2015-09-03莫子杰
莫子杰 陈 浩
(华南师范大学物理与电信工程学院,广东广州 510006)
水星近日点进动问题是广义相对论的几个实验例子中最具有代表性的.在牛顿理论中,如果不考虑其他行星等因素对水星的影响,它绕日运行的是一个闭合椭圆轨道;在考虑了其他行星的摄动等因素影响后,水星近日点存在约5557秒/百年的进动,但得出的进动角仍与天文观测值相差约43秒/百年,这在牛顿理论中难以解释.而爱因斯坦的广义相对论理论则给出了合理的解释,它认为在仅考虑水星绕日运转时,其近日点依然会有进动,其值刚好约43秒/百年,与天文观察值高度吻合.这也成为了广义相对论正确合理的有力证据.
行星近日点的进动角可以由其轨道运行的角频率和周期推出.下面用两种计算方法求解出行星运行的角频率和周期,一种是改进一般文献[1-3]所用的近似求解方法,采用奇异摄动法——PLK方法求解;另一种则通过求解一个特定轨道的椭圆函数解得出,最后也都自然得出进动角.
根据广义相对论,设太阳的引力场为真空静态球对称场并由史瓦西度规描述,则行星的绕日运动满足自由粒子的测地线运动方程,再结合行星运行的守恒定律,可推导得行星运行轨道所依据的微分方程为

1 运用PLK方法近似求解
因为方程非线性项的量级很小,可以用摄动法求出非线性方程的解.一般文献[1-3]用逐次逼近法近似求解,在求解过程中经过多次近似后,求得轨道近似解为其中e为偏心率,轨道角频率为1-3C.然而,这种解法在求解轨道函数u的过程中忽略了里面的一个正比于φ·sinφ的久期项.根据摄动法的要求,由于u对所有的φ在(-∞,+∞)应该是有界的,所以求出来的近似解也应该有界.但久期项的出现使得u不再对所有的φ有界,于是就必然要求φ的取值范围在零的附近时才可略去久期项.但由于行星运行轨道具有的周期性,这里对φ的取值并不必然要限定在某一区间内,因此这里所采用的方法在数学上有局限.关于这一点文献[4]中也有提及,它提出直接找另一个有界的函数来代替这一久期项.
下面,我们提出采用PLK方法来求解式(1),它是一种有效的奇异摄动法,适合用于弱非线性问题.根据PLK方法[5],可把轨道函数和角频率都作渐进展开,这样不仅可避免久期项的出现,使u对所有的φ都有界,而且求解过程不需要再作其他近似便可得出轨道函数的逐级近似解,最后也给出了轨道角频率和周期的表达式.

这里由于C的量级很小,设ε=3C,则可把ε看成是方程中的小参数.再设一新变量为φ=ωφ,把ε和φ代入方程(2)中,有

ω表示运动轨道的角频率.将U和ω分别作摄动展开,精确到一级近似

把展开后的U和ω,即式(4)和式(5)代回到方程(3)中,得到关于ε的零级近似和一级近似方程分别为

由此可首先求解零级近似方程(6),它的解为

其中,a和φ0为由初始条件确定的常数.把零级近似的解(8)式代入一级近似方程(7)中,可得

式(9)右边第二项会诱发久期项.为消除久期项,令它前面的系数为零(非久期条件),即

由式(10)解得ω1=-ω0,进而一级近似方程化为
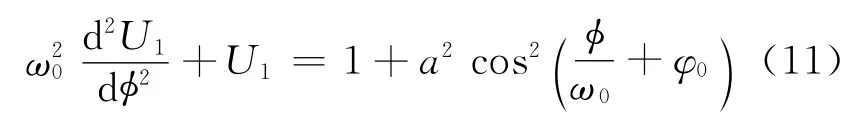
求解方程(11),可得其解为
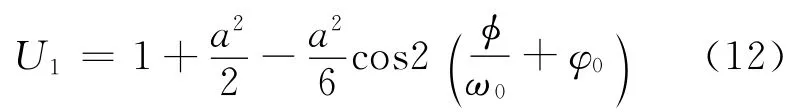
于是微分方程的解U和轨道角频率ω经PLK方法的摄动展开后为

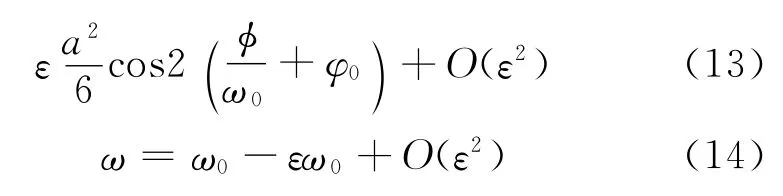

式(16)即为式(15)中余弦函数的角频率,所以得出ω0=1.最后也可以得到轨道周期为
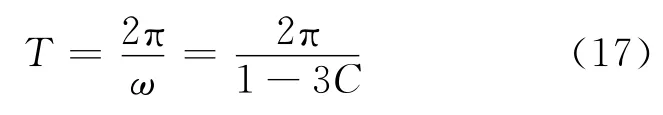
用PLK方法求出来的解不但与一般文献中用逐次逼近法求得的结果一致,而且还可以给出更高阶的轨道修正函数和角频率,清晰地看到轨道函数和角频率经过一级一级的修正展开,加强了研究的精确性和规律探究.加之没有久期项带来的问题,φ在(-∞,+∞)都是有界的,不必作范围限定,更符合数学物理要求.
特别的,这里解到的轨道函数式(15),在略去C2及更高阶项并代入水星运行轨道的参数后,可解得待定常数a即对应为经典椭圆轨道的偏心率e,初相位φ0=0.显然此时轨道函数u(φ)就退化到一般文献[1-3]给出的近似解.
2 求出方程的椭圆函数解
对微分方程(1)式整理后,有

微分方程式(18)可以找到椭圆函数形式的解.但常数P需要由方程(1)的初始条件确定,它与行星的守恒量有关.然而我们注意到,一般在近似求解微分方程(1)得到运动角频率到一级近似值时,并不需要确切给定P的值.我们选一个特殊情况,即令P=0,使得方程(18)可以得出具体的椭圆函数解,进而得出运动角频率和周期.后面可以证明,这样解出来的结果与以往的方法得到的行星进动结论是一致的.
由于此时P=0,故设满足P=0的轨道函数为u′,于是得

式(19)是满足一种特别形式的椭圆方程[5],可以尝试找到它的具体椭圆函数解.整理式(19)有
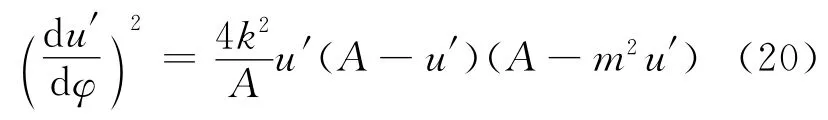
由于C很小,故在m2、A、k2的表达式中,根号内均为正数且小于1.要注意的是,根据椭圆函数的性质,若方程(20)要有椭圆函数解,m2的取值范围应在0到1之间.但现在由于C的量级很小,必然有m2>1,故不能直接得出椭圆函数解,需要先做变量变换.

式(21)右边的m′2的取值范围在0到1之间,故可以得到方程的椭圆函数解为

即有

其中,φ′为常数,式(23)表述的是一种非线性运行轨道.进而可以根据椭圆函数的实周期求出行星运行轨道的周期.在式(23)中,对应椭圆函数的角频率ωe=2mk,椭圆余弦函数和第三类Jacobi椭圆函数的共同实周期为4 K(m′),可得轨道周期为K(m′)为第一类完全椭圆积分,式(24)是行星运行的周期,它是一个非线性运行轨道的周期.
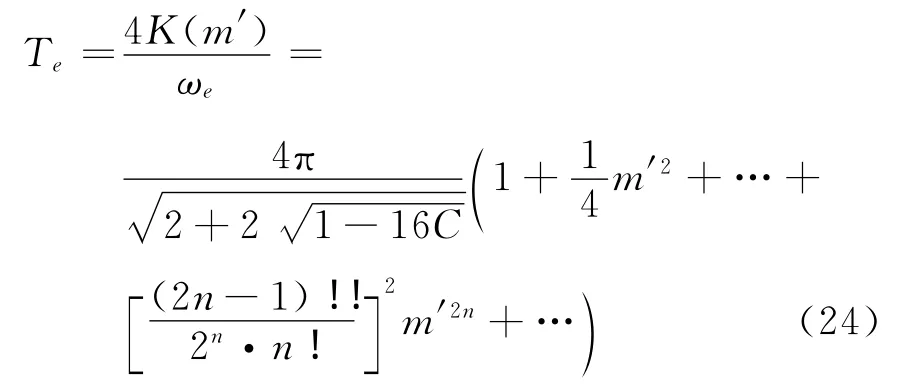
模数m′是一个很小的量,特别的,若模数m′不断减小直至趋于零,则C的值趋于零,椭圆函数趋于极端线性的情况,从式(24)可知此时轨道周期会变为2π,这就等于要求太阳的质量趋于零或行星运动的角动量为无穷大.显然这样的极端线性情况实际是不可能发生的,所以行星运行的进动在自然界中本质上说是一种非线性现象.
3 两种方法求得的角频率联系
运用PLK方法求解得出的结果体现的是一种线性运动解;而在计算u′得到椭圆函数解时,得到的是非线性运动的解.我们知道,行星运行轨道方程为非线性微分方程,PLK方法将非线性方程等效地线性化求解,所以它求解出来的角频率应该理解为是在相同周期的非线性运动下的一个等效线性角频率[5].下面通过定义非线性运动的等效线性角频率,证明在一级近似下,它就是PLK方法求出的角频率ω.
椭圆函数解对应的行星运行周期为式(24).定义等效的线性角频率为ωl,则

因为C和m′都非常小,故将式(25)中的分子、分母的表达式分别做小量展开,略去三阶及以上的项,可得

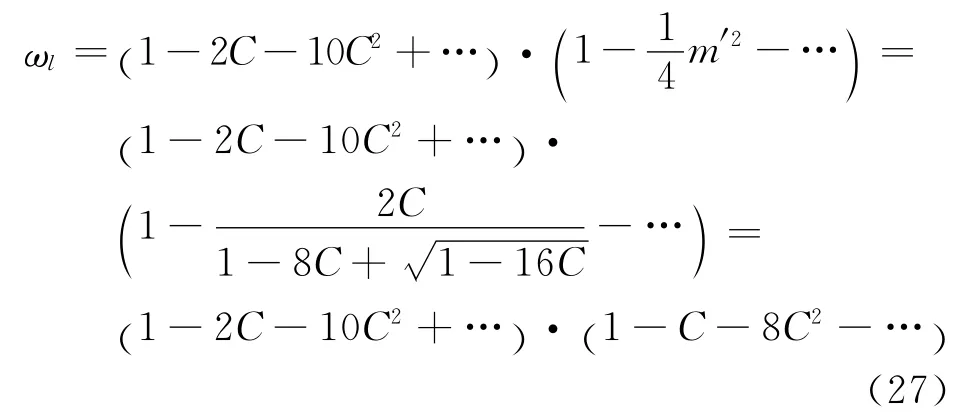
最后略去式(27)展开后C2及更高阶的项,可得

把式(28)与式(16)作比较后易知,这个等效的线性角频率ωl正是用PLK方法求解出来的轨道角频率ω,这也说明了两种计算方法本质上是等效的.
4 水星进动角的结果验证
PLK方法求得的一级近似的轨道角频率表达式(16)与文献[1-3]给出的一致,其计算结果必然也与其得到的结论一致.定义进动角(如图1所示)为Δφ,即有


图1 定义进动角
把水星对应的物理量代入式(29)中,结果就是通常文献给出的水星进动角表达式.
下面来计算由椭圆函数解得的轨道周期表达式得出的水星进动角结果,并可通过天文观测的数值作检验.定义通过椭圆函数解得出来的进动角为Δ′φ,则有
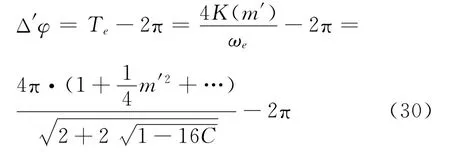
式(30)是进动角的表达式,Δ′φ的单位为弧度/周.对于水星近日点的进动,一般给出的是每百年进动的角度Δφcentury,单位是秒/百年.水星每一百年绕日转过约415周,所以经过代数换算有
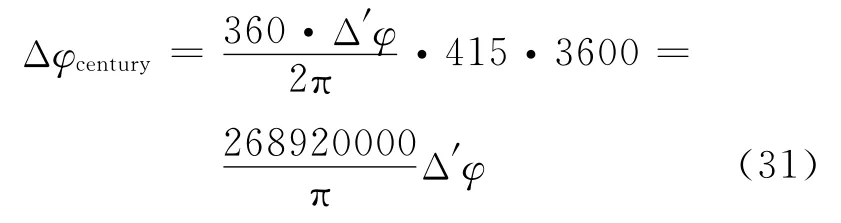
从式(30)可知Δ′φ是与C有关的表达式.略去表达式分子中m′4及以上的高阶项,再将C=中各个对应的物理参数值[6,7]代入式(30)及式(31)后,最后算得具体数值为

根据天文观测的结果,水星近日点每百年的进动角度值应为43.11″±0.45″.而上面计算得到的进动值显然是在观测范围内的,所以说明椭圆函数解的运行周期和进动角表达式是符合事实的.
5 结语
以上的两种求解方法进一步分析了行星的进动问题,并且计算出的相应结果与文献的一致,也符合天文观察事实.有的文献[7-9]通过其他方法,不具体求解轨道角频率和周期也得到近日点的进动角.总之,行星近日点进动的这个问题,由于条件的限制,在计算过程中难免需要通过某些近似或通过调整方程中的参数来求解.当然,基于实验观察数据的精确性,这里的计算结论已为广义相对论提供了有力的证据!
[1]俞允强.广义相对论引论[M].北京:北京大学出版社,1997:91-98.
[2]吴大酞.理论物理(第四册):相对论[M].北京:科学出版社,2010:159-162.
[3]瓦尼安H C,鲁菲尼R.引力与时空[M].向守平,冯珑珑,译.北京:科学出版社,2006:305-309.
[4]Plebanski J,Krasinski A.An Introduction to General Relativity and Cosmology[M].New York:Cambridge University Press,2006:176-182.
[5]刘式达,刘式适.物理学中的非线性方程[M].北京:北京大学出版社,2012:39-135.
[6]付昱华.水星进动问题新解[J].天文学报,1989,30(4):350-354.
[7]温伯格S.引力论和宇宙论:广义相对论的原理和应用[M].邹振隆,张历宁,等,译.北京:科学出版社,1980:220-265.
[8]赵铮,刘辽.广义相对论[M].北京:高等教育出版社,2004:155-160.
[9]王庚,胡跃进.水星近日点进动的建模与摄动解[J].安徽机电学院学报,2000,15(4):19-23.
