两个相依部件并联系统和有冷贮备部件串联系统的模糊可靠性
2015-06-27汪军芳张民悦
汪军芳,张民悦
(兰州理工大学理学院,兰州730050)
两个相依部件并联系统和有冷贮备部件串联系统的模糊可靠性
汪军芳,张民悦
(兰州理工大学理学院,兰州730050)
利用普通可靠性和模糊可靠性的基本理论,建立了两个相依部件并联系统和有冷贮备部件串联系统的模糊可靠性的数学模型,讨论了系统的模糊可靠度、模糊失效率和模糊平均寿命之间的关系,为类似复杂系统提供了更切合实际的系统表述方式。
相依部件;模糊可靠度;模糊失效率;模糊平均寿命
引言
在实际工程中,模糊数学理论应用越来越广泛,随着系统工程日趋复杂,复杂部件的系统也越来越多的运用于工程中。文献[1-4]研究了典型不可修系统的模糊可靠性,文献[5-8]研究了几个典型不可修系统组成的新系统的模糊可靠性,文献[9]是在文献[8]的基础上,对可修的并串联系统进行模糊可靠性研究,文献[10]对冗余系统进行模糊可靠性研究,文献[11-12]对有优先权两部件组成的冷贮备系统和温贮备系统讨论了模糊可靠性。本文将利用以上模型及相应公式,对两个特殊系统:两个相依部件的并联系统和有冷贮备部件的串联系统,进行模糊可靠性分析。
1 模糊条件概率基础
用A表示普通可靠性定义中“产品在规定的使用条件,预期的使用时间内,保持其特定功能”这一清晰事件。Aj表示“第j个部件正常工作”。~A1,~A2,…,~An分别表示各个模糊功能子集所代表的模糊事件。表示~Ai所要讨论的模糊功能子集。显然,A在不同程度上分别属于~A1,~A2,…,~An。由模糊条件概率的定义得
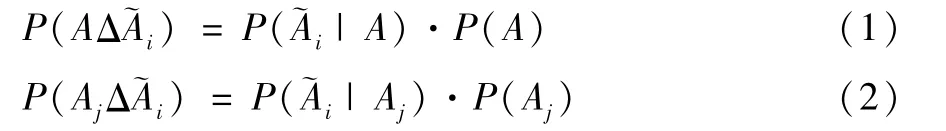
式中,Δ为三角范算子(代数积)。
根据模糊可靠性[13]和普通可靠性[14]的基本理论得
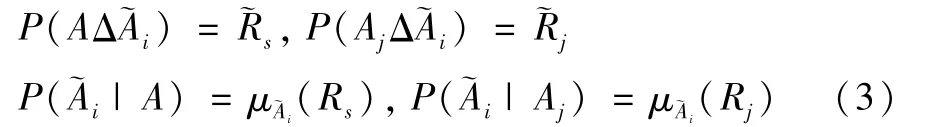

由式(1)-式(3)得i式中,Rs,Rj分别表示系统和第j个部件的清晰可靠度,~Rs,~Rj分别表示系统和第j个部件的模糊可靠度。
由文献[13]知,各部件模糊故障率~λj和普通故障率λj之间的关系:
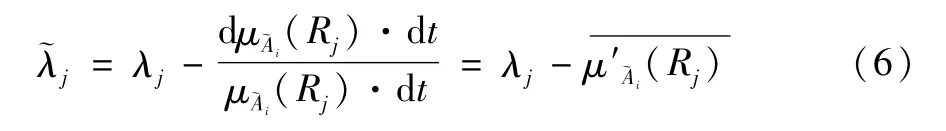
2 两个特殊系统
2.1 两个相依部件的并联系统
系统由两个相依部件并联而成,这两个部件的寿命X1和X2遵从二维指数分布,其联合生存概率为:
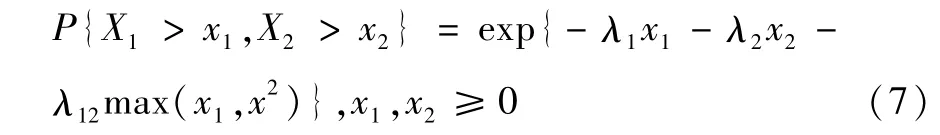
其中,λ1,λ2,λ12>0,因此边缘生存概率为:
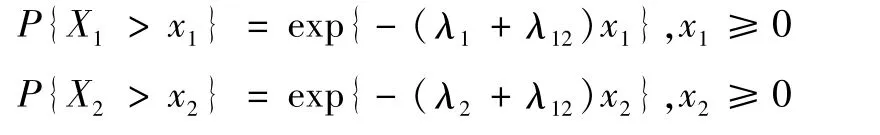
此时,系统的寿命X=max(X1,X2),因此系统的可靠度为:
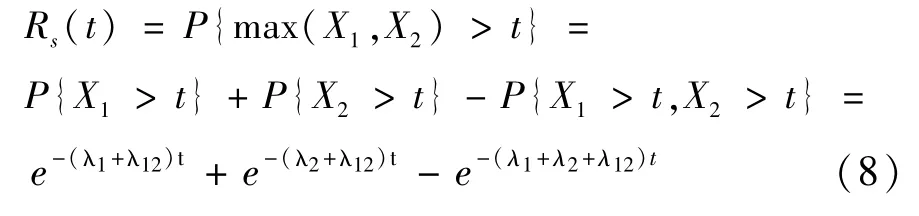
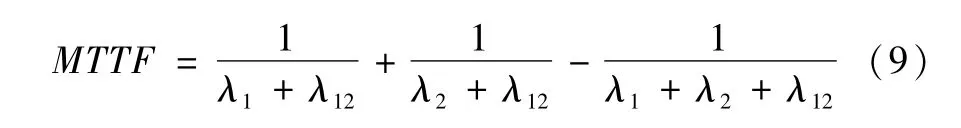
平均寿命:由于两部件的寿命X1和X2遵从二维指数分布,因此

所以,系统的模糊可靠度为:

系统的模糊平均寿命为:

将(6)式代入(11)式得:

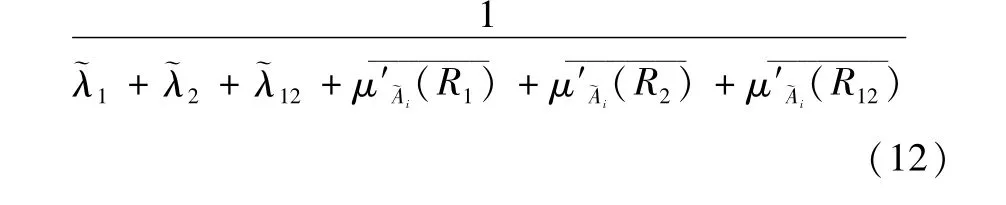
式中,μ~Ai(Rs)m是μ~Ai(Rs)在工作时间的区间[0,∞)上的平均值,它是常数。
2.2 冷贮备部件的串联系统
系统由n+l个同型部件组成,其中系统需有l个部件串联工作,其他部件作冷贮备。当l个工作部件中有一个失效时,若还有贮备部件,则贮备部件之一立即去替换,系统继续工作;当l个工作部件中有一个失效时,若贮备部件已用完,则系统失效。假定所有部件的工作寿命均遵从参数为λ的指数分布,且相互独立。
在一个l个部件的串联系统中,直到有一个部件失效的时间(即串联系统的寿命)分布是1-e-lλt。当其中一个部件失效后,贮备部件之一去替换,替换后仍是l个部件的串联工作。由于指数分布无记忆性,可认为这l个部件都是在新的条件下同时开始工作。因此,直到一个部件失效时间分布仍为1-e-lλt。由于有n次替换,因此系统的寿命是n+1个独立的随机变量之和,每个随机变量的分布均为1-e-lλt。所以,这个系统等价于n+1个独立部件的冷贮备系统,其他每个部件的工作寿命均遵从参数为lλ的指数分布,即Fj(t)=1-e-lλt,t≥0。
假设这n+1个部件的寿命分别为X1,X2,…,Xn+1,且它们相互独立。易见,冷贮备系统的寿命是X=X1+X2+…+Xn+1。
定理1[14]随机变量X1,X2,…,Xn独立同分布Γ(1,λ;t),则X=X1+X2+…+Xn遵从Γ(n,λ;t),其分布函数为:

该系统的可靠度和平均寿命分别为:
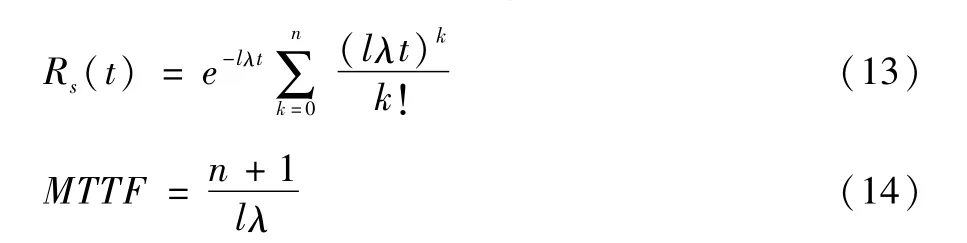
利用各部件普通可靠度Rj(t)与故障率lλ之间的关系Rj(t)=e-lλt,j=1,2,…,n+1,代入(13)式得
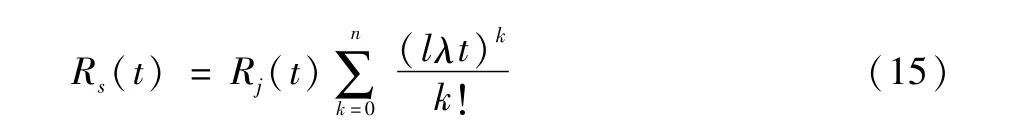
将(5)式、(6)式和(15)式代入(4)式得系统的模糊可靠度为:系统的模糊平均寿命为:
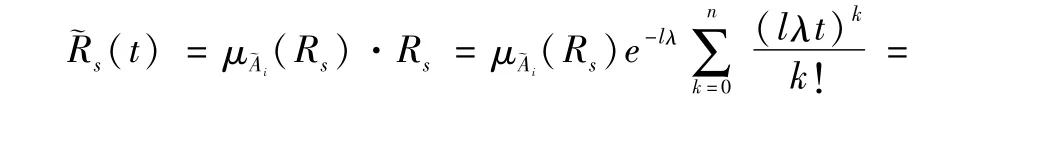


由(6)式得
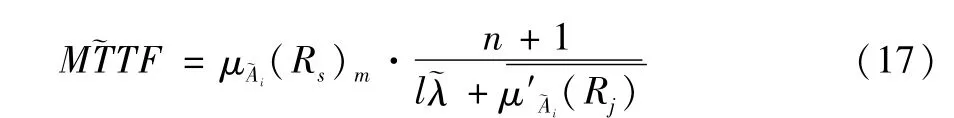
式中,μ~Ai(Rs)m是μ~Ai(Rs)在工作时间的区间[0,∞)上的平均值,它是常数。
3 结束语
随着人们对可靠性研究的不断深入,人们发现许多实际工程问题不仅存在随机性,而且存在广泛的模糊性,特别是在对小样本进行可靠性分析时,模糊性对分析结果起到决定性的影响。因此,人们将模糊理论引入到可靠性的研究中,开展了模糊可靠性的研究[15]。本文的研究结果为类似系统提供了更切合实际的系统表述方法,为人们在实际工程中对类似系统的分析提供一定的指导。
[1]陈胜军,颜梁平.串联系统的模糊可靠性分析[J].现代机械,1997(2):46-17.
[2]李廷杰.表决系统的模糊可靠性[J].系统工程理论与实践,1989(6):13-16.
[3]冷护基,李广安,陈胜军,等.冷贮备系统的模糊可靠性[J].系统工程理论与实践,1997(11):113-123.
[4]冷护基,李广安,颜景平,等.温贮备系统的模糊可靠性[J].机械设计与制造,1998(6):1-3.
[5]姚滔,许芙蓉.多部件温贮备系统模糊可靠性分析[J].长江大学学报,2010,7(2):130-132.
[6]姚滔,张民悦,代文华.混贮备系统的模糊可靠度分析[J].甘肃科学学报,2009,21(4):117-119.
[7]冷护基,李广安,颜景平,等.串-表决系统的模糊可靠性[J].机械设计,1997(3):8-9.
[8]李东娜,张民悦,马长青.并串联系统的模糊可靠性分析[J].甘肃科学学报,2007,19(4):141-144.
[9]马长青,张民悦,李东娜.可修并-串联系统的模糊可靠性分析[J].甘肃科学学报,2009,21(1):143-146.
[10]郭凡,张民悦.两不同型部件冗余系统的模糊可靠性分析[J].沈阳理工大学学报,2012,31(5):84-90.
[11]姚滔,钱存华,刘敏.有优先权两部件冷贮备可修系统的模糊可靠性[J].自动化仪表,2011,32(8):33-39.
[12]包林涛,张民悦,段红星.有优先权两部件温贮备可修系统的模糊可靠性[J].模糊系统与数学,2008,22(1):169-174.
[13]李廷杰,高和.模糊可靠性[J].模糊系统与数学,1988,2(2):11-23.
[14]曹晋华,程侃.可靠性数学引论[M].北京:高等教育出版社,2006.
[15]李廷杰,高和.可靠性设计[M].北京:北航印刷所,1988.
The Fuzzy Reliability of Two Dependent Com ponents of The Parallel System and Series System w ith Cold-store Com ponents
WANG Junfang,ZHANGMinyue(School of Science,Lanzhou University of Technology,Lanzhou 730050,China)
by the help of the basic theories of common reliability and fuzzy reliability,themathematicalmodel to calculate the fuzzy reliability for two dependent components of the parallel system and series system with cold-store components is established.Furthermore,the relationship between fuzzy reliability,fuzzy failure rate and fuzzy average life-span of the system is discussed,which provides amore practical system expression for similar complex systems.
dependent components;fuzzy reliability;fuzzy failure rate;fuzzy average life-span
O213.2
A
1673-1549(2015)01-0080-03
10.11863/j.suse.2015.01.19
2014-11-13
甘肃省自然科学基金(3ZS042-B25-016)
汪军芳(1987-),女,甘肃天水人,硕士生,主要从事可靠性理论方面的研究,(E-mail)554624664@qq.com张民悦(1958-),男,河南南乐人,教授,主要从事可靠性理论方面的研究,(E-mail)zhangminyue@lut.cn
