椭圆型最优控制问题中的L1，2－方向稀疏

严春梅，张维

（成都理工大学管理科学学院，成都610059）

椭圆型最优控制问题中的L1，2－方向稀疏

严春梅，张维

（成都理工大学管理科学学院，成都610059）

介绍一种带有L1，2－方向稀疏项的椭圆型最优控制问题，分析条纹稀疏模式，从理论角度研究该问题的一阶最优性条件。为解决不可微控制问题，基于广义微分，提出一个半光滑牛顿方法，将问题在泛函空间中进行表示和分析，并具有局部超线性收敛率。

方向稀疏；非光滑正则化；半光滑牛顿

引言

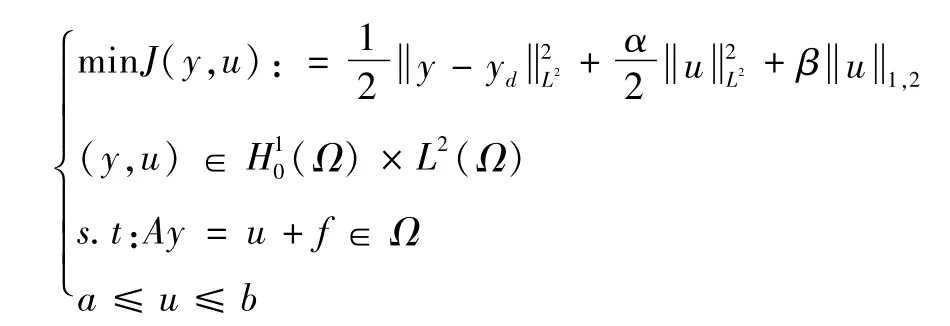
罚项是L1类型的最优控制问题能产生稀疏解［1］。即控制函数在区域的某些部分为0，因为在这些点，不必要应用控制。分析一个带有稀疏测度的椭圆型问题，稀疏测度能够促进条纹稀疏模式。考虑带有条纹稀疏模式的椭圆型的最优控制（p）问题：Ω∈Rn是一个有界区域，带有足够光滑的边界Γ＝∂Ω，yd，a，b∈L2（Ω），且在Ω上几乎处处有a＜0＜b，α，β≥0。A：H10（Ω）→H－1（Ω）是二阶线性椭圆型微分算子，并且和分别代表L2（Ω）和L1（L2（Ω））范数，y是状态，u是控制变量，yd是理想状态。

非光滑项在偏微分方程（PDE）的最优问题中经常被用于反问题的正则化，如处理图像过程［2］。文献［3］，L1－正则化被使用在PDE的最优控制背景下。文献［4］分析了带有非方向稀疏项的椭圆型最优控制问题。除稀疏项外，L2范数的平方是成本函数的一部分，它允许问题在Hilbert空间结构下被分析，用牛顿类型算法解决［5］。方向稀疏项在2012年被Heraog R［6］第一次提出，从理论到数值的实现都具有很大的难度，本文在此基础上研究椭圆型问题的方向稀疏项，着重研究其理论和计算方法。

1 预备知识

空间Ω⊂RN，N≥2是一个有界可测集，可以RN＝Rn×RN－n（1≤n＜N）将其按坐标分割。故有集合：

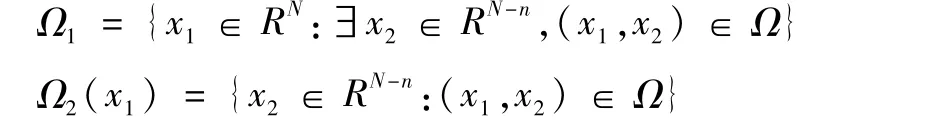
Ω1可以看作Ω在RN上的射影，Ω2（x1）是Ω在x1∈ Rn方向的横截面。方向稀疏项的一般形式为：

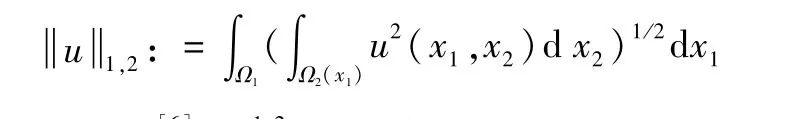
引理1［6］L1，2的对偶空间是Bochner类型空间L∞，2。L∞，2是定义在Ω上的所有测度函数φ且是有限的。

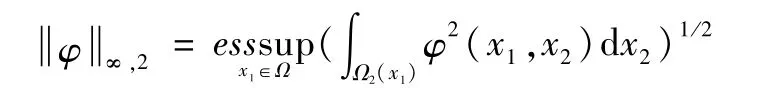
引理2［6］在u∈L1，2（Ω）的次微分为：L2（Ω2（x1））范数的次微分为：

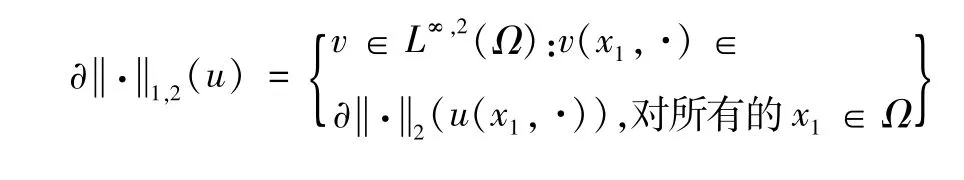
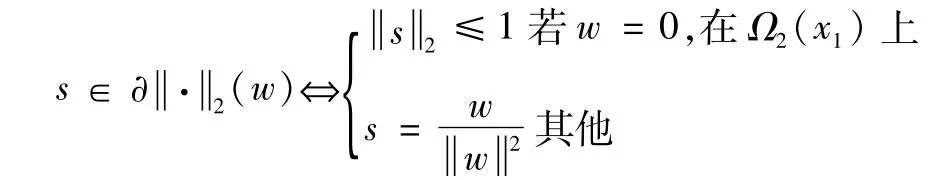
2 一阶最优系统

用一个减少公式的问题替换（p）。这个问题的减少仅仅涉及到控制变量u，因为微分算子A存在逆映射A－1：H－1（Ω）→H10（Ω），则减少后的问题是（＾p）：

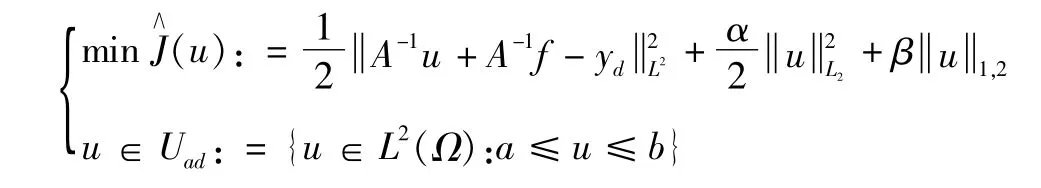
这是一个在Hilbert空间上凸的最优性问题。

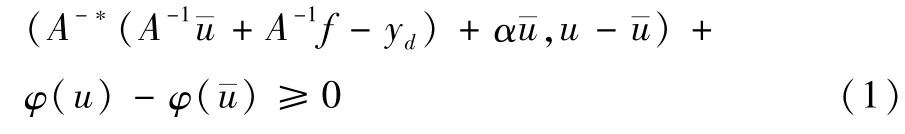
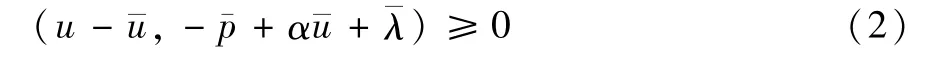
对所有的u∈Uad都成立，其中，伴随状态¯：＝－），次微分?。

变分不等式（2）式几乎需要在所有的地方进行逐点讨论。但在文献［7］允许存在非负函数和在中起到不等式约束的拉格朗日乘数，而且估计微分¯λ∈涉及到¯u的符号，由此引进拉格朗日乘数和则变分不等式（2）式变为：

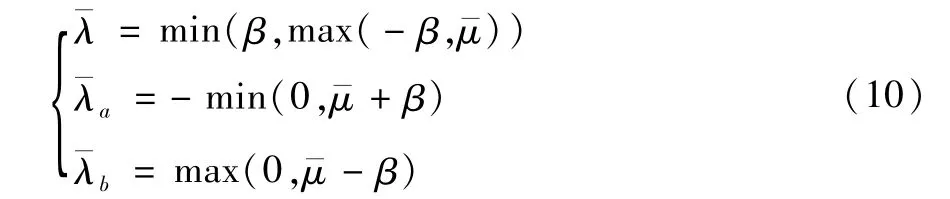
用（9）式和（10）式替换（4）－（8）式，对于c＞0，则替换后的系统为非光滑方程：

因此，最大、最小函数就可以被理解为逐点。

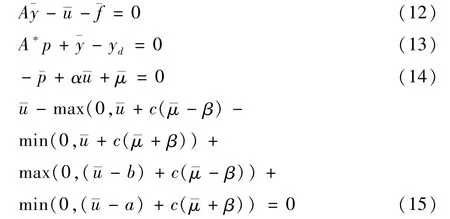
其中，c＞0，可以得到无方向稀疏项的（p）的最优性条件，就是令β＝0，则（12）－（14）式仍然保持不变，（15）式变为：

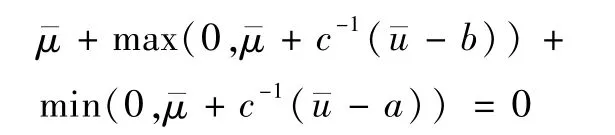
已经用于构建一种算法，应用于双边控制约束最优控制问题。

3 半光滑牛顿法

半光滑牛顿方法研究有限维函数空间，常用于最优控制问题。在确定条件下，局部超线性收敛甚至全局收敛性都可以被证明。

X，Y是Banach空间，D⊂X是开的，F：D→Y是非线性映射。映射F是在开集U⊂D中是广义可微的，若存在一个映射g：U→L（X，Y），对每个x∈U，都有：

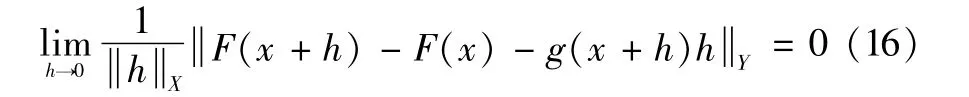
假设用牛顿迭代法发现半光滑映射F（x）＝0的一个根¯x。则下面局部收敛性结果成立。

定理2［8］假设¯x∈D是F（x）＝0的一个解，F在¯x的一个开领域U内是半光滑的，且有广义微分g。若对所有的x∈U，g（x）－1都存在｝是有界的，初始值x0∈U已知，则牛顿迭代xk＋1＝xk－g（xk）－1F（xk）是定义明确的，如果x0足够的接近¯x，则具有超线性收敛率。

用牛顿法求解（12）－（15）式的解，需要半光滑的逐点的最大和最小算子。它们的定义为

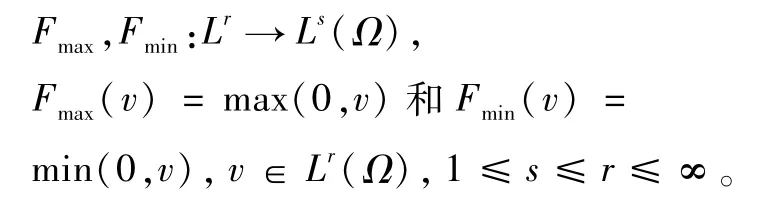
映射：

可以作为Fmax，Fmin在v处的广义导数。

由（14）式可以推出¯μ＝¯p－α¯u，代入（15）式中，并令c：＝α－1，则有

由于c的选择［9］，只有¯p出现在逐点的最大和最小算子中，且¯p具有更多的规律性。为了更加明确，引进算子：

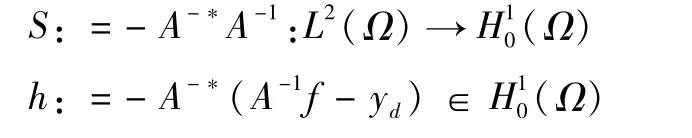
则¯p：＝－A－*（A－1¯u＋A－1f－yd）可以写成¯p＝S¯u＋h。考虑映射T：L6，2（Ω）→Ls（Ω），

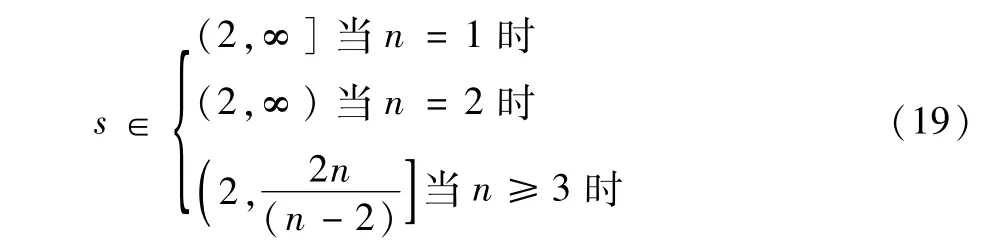
定义Tu＝p＝Su＋h。严格的说，Tu＝I（Su＋h），I表示H10（Ω）嵌入到Ls（Ω）中。可以知道T是定义明确的，且是连续的。由于它是仿射，所以它也是Frechet可微的。用T¯u替换（18）式中的¯p，定义）

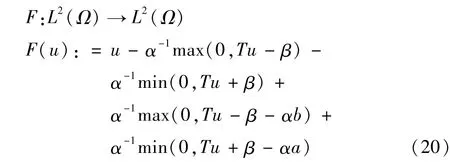
紧凑的形式F（u）＝0表示最优系统（12）－（15）式。讨论函数F的广义可微性，并用牛顿迭代法求解F（u）＝0，即为（p）问题的解。

定理3如（20）式定义的函数F是广义可微的，广义导数为：

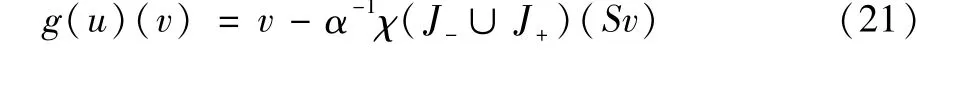
其中，J－，J＋是互不相交的集合：

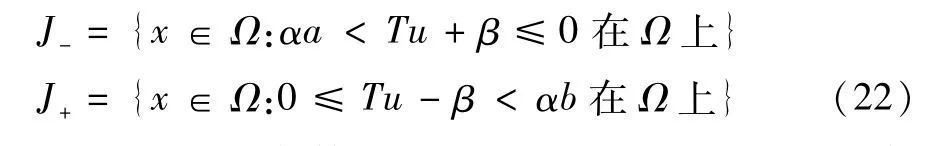
证明因为放射算子T具有光滑性性质，则对于每一个u∈L2（Ω）都有Tu∈Ls（Ω）（s＞2）。这表明映射

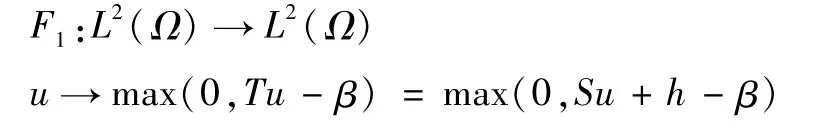
是光滑的，此外，F1的广义导数为g1（u）（v）＝χA（Sv），χA代表集合A＝｛x∈Ω：Tu－β≥0在Ω上｝的特征函数。在（20）式中，最大和最小函数可以进行类似的讨论。可以得出整个函数F是广义可微的合并特征函数，可以得到F的广义导数为（21）式。证毕。

求解（p）问题具体算法（半光滑牛顿算法）。（1）给出初始值u0∈L2（Ω）并令k：＝0。（2）除非某些停止准则是满意的，否则计算广义导数g（uk），导出δuk，更新uk＋1：＝uk＋δuk，令k：＝k＋1，并回到第一步。

应用定理2的半光滑牛顿算法的结果是收敛的。

定理4初始值u0足够靠近（p）的解¯u，则半光滑牛顿法迭代的uk在L2（Ω）中超线性收敛于¯u。而且，相应的状态yk在H10（Ω）中超线性收敛于¯y。

使用的半光滑牛顿方法服从有效集的设置。与半光滑牛顿方法有关的“双重有效集”［10］和“非有效集策略”［11］已经被广泛的讨论和应用。

4 结束语

本文从理论上分析了方向稀疏椭圆型最优控制问题，该问题可以被基于广义微分的半光滑牛顿法解决，且具有超线性收敛率。进一步的研究可以用双重有效集法。方向稀疏项为L0，2类型的偏微分最优控制问题是非凸且高度非线性的，至今还有待解决。

［1］Nikolova M.Analysis of the recovery of edges in images and signals by minimizing nonconvex regularized leastsquares［J］.Multiscale Model，2005，4（3）：960-991.

［2］Troltzsch F.Optimal Control of Partial Differential Equations：Theory，Methods and Application［M］.Providence：American Mathematical Society，RI，2010.

［3］Clason C，Kunisch K.A duality-based approach to elliptic control problems in nonreflexive Banach space［J］. ESAIM ControlOptimal，2011（17）：243-266.

［4］Wachsmuth G，wachsmuth D.Cocergence and regularization results for optimal control problems w ith sparsity functional［J］.ESAIM Control optimal，2011（17）：858-886.

［5］Casas E，Herzog R，Wachsmuth G.Optimality conditions and error analysis of semilinear elliptic control problems w ith L1 cost functional［J］.SIAM J，Optimal，2012，22（3）：795-820.

［6］Herzog R，Stadler G，Wachsmuth G.Directional sparsity in optimal control of partial differential equations［J］. SIAM Journalon Controland Optimization，2012，50（2）：943-963.

［7］Troltzsch V F，W iesbaden.Optimal Steuerung partieller Differentialgleichungen［M］.W iesbaden：Vieweg，2005.

［8］Sun D，Han J.New ton and quasi-New ton methods for a class of nonsmooth equations and related problems［J］. SIAM J.Optimal，1997（7）：463-480.

［9］Hintermüller M I，Kunisch K.The primal-dual active set strategy as a semi-smooth New ton method［J］.SIAM J. Optimal，2003，13（3）：865-888.

［10］Davis T A，Hager W W.A sparse proximal implementation of the LP dualactive set algorithm［J］.Math.Program-Mathematical Programming，2008，112（2）：275-301.

［11］Ito K，Kunisch K.The primal-dualactive setmethod for nonlinear optimal control problems w ith bilateral constraints［J］.SIAM.Control.Optimal，2004，43（1）：357-376.

L1，2-Directional Sparsity of Elliptic Optimal Control Problem s

YAN Chunmei，ZHANGWei
（School of Administrative Science，Chengdu University of Technology，Chengdu 610059，China）

The elliptic optimal control problemswith L1，2-directional sparsity are introduced and the stripe sparsemode is analyzed.Emphatically，the first-order optimality conditions of the problem are studied from the theory angle.For solving the non-differentiable control problem，a semi-smooth Newton method based on the generalized differential is proposed，with which the problem can be stated and analyzed in the functional space and has local superlinear convergence rate.

directional sparsity；non-smooth regularization；semi-smooth Newton

O29

A

1673-1549（2015）01-0076-04

10．11863／j．suse．2015．01．18

2014-08-09

严春梅（1992-），女，四川宜宾人，硕士生，主要从事应用泛函分析方面的研究，（E-mail）yanchunmei199202＠163.com