VaR准确性检验的T检验法
2015-06-27唐宁冯长焕
唐宁,冯长焕
(西华师范大学数学与信息学院,四川南充637002)
VaR准确性检验的T检验法
唐宁,冯长焕
(西华师范大学数学与信息学院,四川南充637002)
根据VaR失败率检验法的定义,通过利用组合的方式获取检验样本和构造服从T分布的统计量,得到检验VaR准确性的新方法——T检验法。T检验法所接受的模型不仅在似然比检验法下能被接受,且在同一置信度下T检验法所接受的模型比似然比检验法所接受的模型的准确性更高。最后通过实证分析进一步说明T检验法比似然比检验法能更好地检验VaR的准确性。
失败率检验;VaR;T检验
引言
VaR(value at risk)字面解释就是“在险价值”,其含义指:在市场正常波动下,在一定概率水平(置信度)下,某一金融资产或证券组合价值在未来特定时期内的最大可能损失。因VaR的大小直接关系着金融投资者的利益,故关于VaR的计算方法也在不断完善。不管是最初的历史模拟法、方差-协方差法和蒙特卡洛法,还是现在已经完善的极值理论法计算出的VaR都是一个估计值,故对VaR准确性的检验就显得尤为重要。而对于VaR准确性检验的方法主要有失败率检验法、正态检验法、似然比检验法和贝叶斯检验法[1-2](其中似然比检验法最常用),都是通过把检验失败率转化为检验失败次数来检验VaR准确性。正态检验法和似然比检验法这两种方法都是以失败次数N服从二项分布B(T,p)(其中T为实验总天数,p为失败率)为出发点。其中正态性检验是当T充分大时,由中心极限定理得出统计量

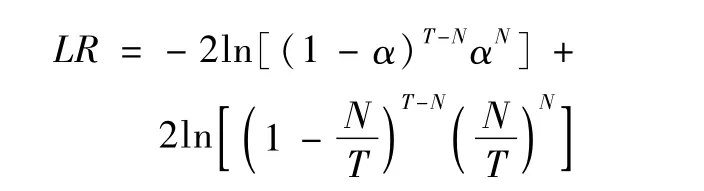
服从标准正态分布,从而得到失败次数N的接受域。似然比检验是由统计量[3]的极限分布,是自由度为1的χ2分布得到失败次数N的接受域(α是置信水平)。从正态检验法和似然比检验法可看出,两种方法都是在大样本的前提下得出的结果,且这两种检验方法不可避免的问题是:虽然总的失败次数落在接受域内,但是失败是连续出现在一段时间内,而未失败的VaR又连续出现在另一段时间内,即预测的失败具有前后相关的关系,那么,仍不能说相应的VaR模型可靠,而利用正态检验法和似然比检验法都不能拒绝此模型。针对这一问题,本文直接从失败率的定义出发,构建了在大样本和小样本情况下均适用的T检验法来检验VaR准确性。
1 失败率检验法定义
VaR的准确性通常是利用失败率来衡量。当在置信水平α下估计出VaR时,将t时刻的损失与t时刻的VaR进行比较,如果损失大于VaR,则记为失败。若总天数为T的实验中,其失败的天数为N,则失败率p记为:p=,而失败率检验的定义为:将失败率p与置信水平α(α=1-c,c为置信度)进行比较,若p=α,则说明估计出的VaR比较准确,相应的VaR模型较好[3]。相反,若p值与α相差较大,则说明估计出的VaR不可靠,相应的VaR模型存在不足。然而通常情况下,可能会因为原始数据的选取和随机误差项干扰等因素使得失败率p与置信水平α不是绝对相等,就不能说明估计出的VaR不可靠,故需要对p与α是否具有显著性差异进行检验。
2 T检验
2.1 T检验原理
从失败率检验的定义可知,希望得到的失败率p与置信水平α不具有显著性的差异。然而,对所有数据进行样本内检验时,得到的某个特定的失败率p大多情况下与α是不同的,即使p与α相同,但又因为预测失败可能存在前后相关关系,所以不能轻易得出模型是否可靠的结论。为了解决这一问题,可以选取不同时间段数据作为检验样本或者选取不同的样本容量,如果得到的p值与α均无显著性差异,那么就可以说估计出的VaR比较准确。但是因数据选取等偶然性原因,很难使每个p都与α均无显著性差异,所以对于选择n个检验样本得到的n个p(这n个失败率p中有些p值相同有些不同),只要它们的均值¯p与α没有显著性差异就可以说估计出的VaR比较准确。
对于成立时间较长的金融行业,它具有充足的历史数据,既可以选择不同时间段的数据作为检验样本也可以改变样本容量获得多个p值,但是对于发展历史较短的行业,能够利用的历史数据有限,得到的p值数据很少,这样就会因偶然性得出与实际情况不一致的结果。为了克服小样本数据不足对结果造成的影响,选取检验样本可按随机抽取的方式进行,即:如果共有n个历史数据,那么从中随机抽取适当数据(记为m个,m<n),重复抽取k次,即可得到k个p值(这些p值可能相同也可能不同),按照随机抽取的方法,由组合原理知一共可抽取Cmn个不同的样本,即可得到Cmn个p值,增加了检验样本。
设p1,p2,...,pn是由随机抽取的方式得到的n个p值,¯p是这n个p值的均值,若¯p与α没有显著性差异,那么由统计学原理可知统计量

应该服从自由度为(n-1)的t分布[4](其中s为样本p1,p2,...,pn的标准差),那么对于给定的假设检验显著性水平ξ,¯p的接受域为:

故当检验VaR准确性时,只要¯p落在该接受域内,则称¯p与α无显著性差异,即估计出的VaR具有较高的准确性,反之,若¯p落在了接受域外,则说明¯p与α显著不同,相应的VaR具有高估或低估价值风险的嫌疑,故估计出VaR的VaR模型有待进一步改善。通过此方法可以克服预测失败存在相关关系对模型优良判断的影响。因为此检验方法是构造服从t分布的统计量T,所以将此种方法称为T检验法。
2.2 实证分析
选取上证指数2013年1月4日至2014年1月28日的257个日收盘价为样本,经

(Pt为资产在t时刻的价格)处理后得256个数据。利用eviews6.0对序列Xt进行一系列相关的分析后建立EGARCH模型[5]为:

由风险价值VaR的定义可得VaR在统计学上的定义为[6]:
其中,Rt为资产在第t期的收益率,VaRt为t时刻α显著水平下的VaR,取值为正。
2.2.1正态假设下T检验法与似然比检验法比较
为了计算VaR,假设序列Xt服从正态分布,则VaRt=ut+σtZ1-α,其中,ut和σt分别是t时刻Xt序列的均值和标准差。结合已建立的EGARCH模型得到的σt可得99%置信度下255天的VaR(表1)。
通过失败率检验,总天数为255天的VaR中失败总天数为5天,该值落在Kupiec提出的似然比检验法下的接受域(0,7)内,即似然比检验结果说明在正态假设下计算出的VaR可靠。

表1正态假设下的部分VaR值
T检验法检验:在255天中随机抽取100天并计算这100天内的失败率,重复抽取30次,得到30个失败率p,对这30个p值进行均值是否为0.01的T检验[7],检验结果(表2)显示Sig.值为0.000,说明这30个失败率p的均值与0.01存在显著性差异。即:T检验法的检验结果为正态假设下计算出的VaR不可靠,还有待改进。

表2正态分布下T检验结果
分析T检验法拒绝正态假设下的VaR模型的原因:(1)对Xt进行统计分析发现Xt序列的偏度为0.327 529,峰度为5.320 699,且JB统计量的伴随概率为0.000,即Xt不服从正态分布,T检验法拒绝正态假设下的VaR模型正好与Xt实际不服从正态分布相吻合。(2)从T检验法的检验样本获取方法可知,T检验法是拒绝失败的发生具有前后相关关系的模型,而正态分布下总数为255天的5次失败主要发生在前110天内,所以T检验法拒绝相应的VaR模型。
2.2.2极值理论下T检验法与似然比检验法比较
首先对收益率序列建立EGARCH模型,再对残差建立极值模型,最后根据收益率序列的VaREGARCH与经EGARCH模型过滤后得到的残差序列的VaRε之间的关系:VaREGARCH=μt+σtVaRε[3],计算到99%置信度下255天的VaR,见表3。

表3极值理论下的部分VaR值
经检验,255天中共有3天失败,该值也落在似然比检验法下的接受域内,说明运用极值理论计算出的VaR通过了似然比检验,即极值理论下的VaR模型可靠。同样在255天中随机抽取100天计算失败率,重复30次,对得到的30个失败率p进行均值是否为0.01的t检验[7],检验结果(表4)的Sig.值为0.083,说明这30个失败率p的均值与0.01无显著性差异。故通过T检验法检验,表明在极值理论下计算出的VaR可靠。
T检验法接受极值理论下的VaR的原因是:(1)VaR主要研究极值,所以利用极值理论计算结果比正态假设更加准确,且本文不是直接对Xt序列建立极值模型,而

表4极值理论下T检验结果
是对经过EGARCH模型过滤后得到的残差序列建立极值模型,这样更能满足极值理论需序列独立同分布这一条件。所以在理论上极值理论的VaR模型可靠,而T检验结果与此相符。(2)极值理论下总数为255天的3次失败分别发生第29、36和108这3个交易日内,可认为失败的发生不具有前后相关关系,所以T检验法接受相应的VaR模型。
3 结束语
本文根据失败率的定义确定了检验VaR准确性的T检验法,利用组合的方式获取检验样本和构造统计量得到了失败率均值¯p的接受域,通过上证指数的应用比较发现:在99%置信度下,T检验法拒绝了似然比检验法所接受的正态假设下的VaR模型,这一结果与序列不服从正态分布相吻合,说明在同一置信度下T检验法比似然比检验法对模型的准确性要求更高,且在99%置信度下,T检验法和似然比检验法都接受了极值理论下的VaR模型,这说明T检验法能接受较好的模型。总之T检验既能拒绝有待改进的模型又能接受较好的模型,能达到检验VaR准确性的目的。
[1]王向翠,董佳慧.VaR准确性检验的贝叶斯方法[J].企业技术开发,2009,28(10):44-45.
[2]杨永愉,丁进,杨凡.VaR模型后验测试的贝叶斯方法[J].统计与决策,2005(1):4-7.
[3]俞慧琴.基于极值理论VaR模型的上市公司行业风险比较研究[D].浙江:浙江大学,2013.
[4]茆诗松,程依明.概率论与数理统计教程[M].北京:高等教育出版社,2010.
[5]董银霞.上证综指基于ARCH模型的VaR风险价值测度分析[J].会计之友,2014(11):70-75.
[6]余素红,张世英,宋军.基于GARCH模型和SV模型的VaR比较[J].管理科学学报.2004,7(5):61-66.
[7]马庆国.应用统计学:数理统计方法数据获取与SPSS应用[M].上海:科教出版社,2005.
[8]郭玮如.VaR最适计算方法之选择[D].台湾:国立台湾大学,2011.
[9]阳异.风险价值(VaR)估计方法的优化改进及其在上证指数上的应用[D].成都:西南财经大学,2011.
[10]杨继平,袁璐.基于结构转换非参数GARCH模型的var估计[J].管理科学学报,2014,17(2):69-80.
[11]罗攀攀.基于EVT的ARMA-EGARCH-M模型的VaR研究[D].南昌:南昌大学,2013.
The T-test of VaR Accuracy Test
TANG Ning,FENG Changhuan
(School of Mathematics and Information,China West Normal University,Nanchong 637002,China)
According to the definition of VaR failure test,a new method to test the accuracy of VaR is obtained,which using combination method to get testing samples and structure statistics that obey T distribution,that is T-test.Themodel accepted by the T-test can also accepted by likelihood ratio test,and at the same confidence,it ismore accurate.by the end,through the empirical analysis,it is further explained that,compared to the likelihood ratio test,T-test can test the accuracy of the VaR preferably.
failure test;VaR;T-test
F224.7
A
1673-1549(2015)01-0083-04
10.11863/j.suse.2015.01.20
2014-12-11
西华师范大学基本科研业务费专项资金项目(14C004);南充市社科规划项目(NC2013B027)
唐宁(1991-),女,四川蓬安人,硕士生,主要从事统计学理论及应用方面的研究,(E-mail)422706724@qq.com
