风电机组变桨距系统的反推滑模控制

廖茜，邱晓燕，江润洲，王刚，李卓艺

（四川大学电气信息学院智能电网四川省重点实验室，四川成都610065）

1 引言

风力发电被认为是一种具有广泛应用前景的新能源。但由于风速的随机波动性，风力发电机组输出功率会随风速的变化大幅波动，无法满足风机并网要求。当风速高于风机额定风速时，风电机组改变浆距角使其保持稳定的功率输出。因此，研究风电机组的变桨距控制系统具有重要意义。

近年来，国内外学者对变桨距控制策略例如协调控制［1］、模糊控制［2］、分段PI 控制［3］、滑模控制［4］、神经网络控制［5］等进行了深入研究。其中滑模变结构控制由于具有良好的鲁棒性、易于实现等优点，被广泛用于风电机组变桨距控制系统中［6-8］。尽管传统滑模控制有良好的鲁棒性，但不能保证系统状态在有限时间收敛到平衡原点，因此过快的风速波动会影响系统的稳定性。而抗干扰能力强、响应速度快的反推控制可以弥补传统滑模控制的这些缺陷。反推控制［9-10］是在逐步递推的过程中引入中间虚拟控制量，并基于Lyapunov 稳定性理论设计整个系统控制器。由于其具有良好的动态性能而被广泛用于风力发电系统控制［11-14］。但它存在计算复杂等问题，这使得控制器难以实现。

本文将滑模变结构控制和反推控制结合设计控制器。这样不但可以改善系统动态性能，保证系统的稳定性，而且可以避免传统反推设计方法计算复杂的问题。为了将滑模变结构控制和反推控制结合，本文针对风力发电系统的平衡点随风速变化的情况，先将其非线性模型进行全局线性化处理。经过全局精确线性化处理，原坐标下的复杂非线性系统转化为新坐标下的简单线性系统从而实现对系统各个运行点实行精确控制。再在EFBL的基础上，将滑模变结构控制和反推控制结合设计风电机组变桨距控制器。通过与SMC 进行对比仿真，结果表明：该控制器能迅速、有效地使系统达到稳定，并实现风电机组的恒功率控制。

2 风力发电系统建模

2.1 风机模型

变速变桨距风机的模型［15］为

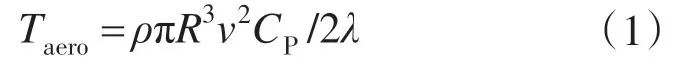
式中：Tareo为风机机械转矩，是整个系统的驱动力矩；ρ为空气密度；v为风速；R为风轮半径；λ为叶尖速比，λ=ωrR/v；CP为功率系数（风能利用系数）。采用CP为

其中

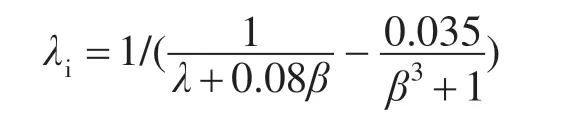
式中：β为浆距角。

风电机组的能量转换关系为

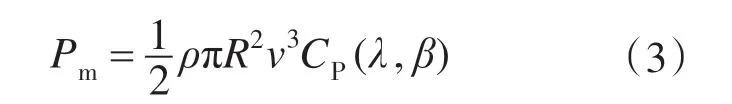
式中：Pm为风机捕获的风能。

由上式可知风机捕获的风能在很大程度上取决于风机的功率系数CP。风能利用系数CP的曲线见图1。

图1 风能利用系数CP曲线图Fig.1 Curves of wind power utilization coefficientCP

由图1 可知，随着浆距角β的增大，功率系数CP逐渐减小。因此变桨距风力发电机通过调节浆距角β以改变功率系数CP，从而改变风力发电系统的输出功率。

2.2 传动系统模型

风力发电机组的传动系统数学模型可表示为

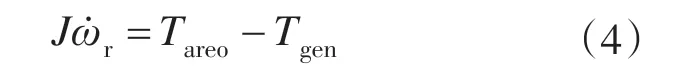
式中:J为风力机和发电机的总转动惯量；ωr为风机转速；Tgen为发电机电磁转矩。

2.3 变桨距执行机构模型

将浆距角执行机构假定为一阶惯性环节，表示为

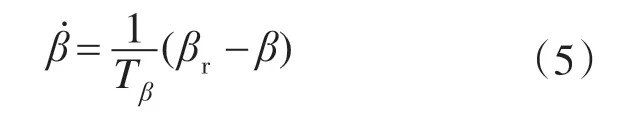
式中：Tβ为时间常数；βr为控制量，βr=u。

由于存在滞后，测速装置用惯性环节表示：

式中：ωrm为速度传感器测得的风机的角速度；Tω为时间常数。

式（4）～式（6）构成风电机组的3 阶非线性模型，其中状态变量有风轮转速ωr，桨距角β，风机的测量转速ωrm。

3 风电机组的反推滑模控制器设计

3.1 风力发电系统

风力发电系统主要由风轮机、传动系统、发电机、变换器、电网和控制器组成，其控制结构框图如图2所示。风电机组在高风速下的控制目标为保持恒功率输出，控制手段即维持电磁转矩和风机转速在额定值附近。本文主要研究内容为变桨距控制，故将电磁转矩设定为恒值，通过控制转速从而实现恒功率控制。

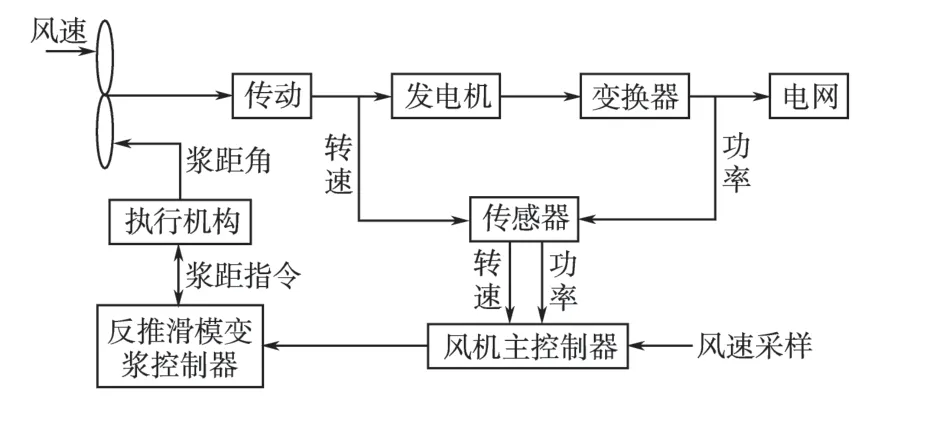
图2 风电机组的变桨距控制结构框图Fig.2 Variable pitch control block of a wind turbine

3.2 风电机组模型的精确反馈线性化

如前所述风电机组模型为3 阶非线性模型，需要使用EFBL 对其进行处理。经EFBL 处理后模型可以避免复杂的计算，又可避免传统泰勒展开式进行局部线性化近似带来的不精确问题。EFBL的基本原理是通过适当的非线性状态和坐标变换，将复杂的非线性问题转化为新坐标下的简单的线性问题。经坐标变换后的线性系统是全局精确线性化的，这样就可避免传统泰勒展开式进行局部线性化近似带来的不精确问题。

结合风电的自身情况，风力发电系统的平衡点随着风速的变化而改变，基于某一工况点附近的传统局部线性化近似模型设计出的控制器并不能满足大范围扰动下的控制性能。而经过EFBL处理的全局精确线性化模型能有效克服这一不足，满足大范围扰动下的控制性能。

本文基于EFBL的原理，将式（4）～式（6）改写成X˙=f(X)+g(X)u的形式，对风电机组非线性模型进行全局线性化处理，从而对系统各个运行点实行精确控制。其中：

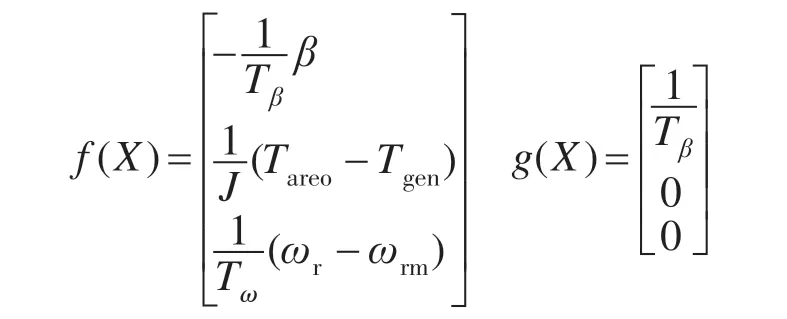
1）检验可行性。令ωrm0为风机额定转速，本系统控制目标为ωrm-ωrm0=0，故选定h(X)=ωrm-ωrm0为其输出函数，经计算可得：。因此系统的关系度r=3=n，满足EFBL的条件，可进行坐标变换。

2）进行坐标变换。选取合适的状态反馈，得：

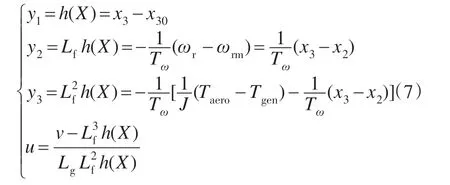
则风电机组的非线性模型转化成完全可控的Brunovsky标准型：

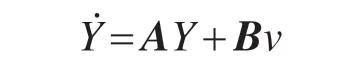
其中

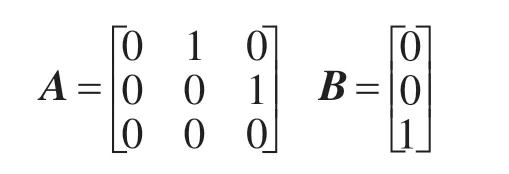
通过上述计算分析，就可将在原坐标下的复杂的3阶非线性系统转化为新坐标下的简单的3阶定常线性系统。这样一旦确定了新坐标系统的系统控制量v，就可确定原控制量u。

3.3 BSMC的设计

针对风速的随机波动性，本文用反推控制方法设计反推控制器，并将滑模控制与之有机结合，令各个状态变量的跟踪误差为

式中：α1，α2为递推过程中的虚拟控制量。

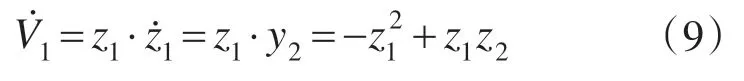
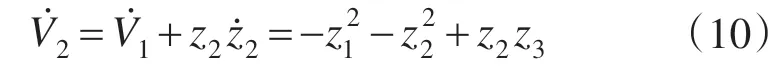
第3步：选择非线性系统滑模面为

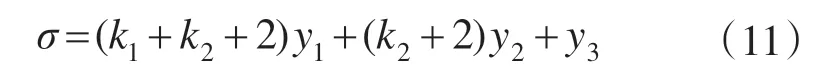
采用变结构控制理论中指数趋近律的设计方法，令

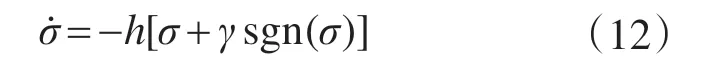
根据反推定理，由式（8）～式（11）可以计算出非线性系统的反推滑模控制器为

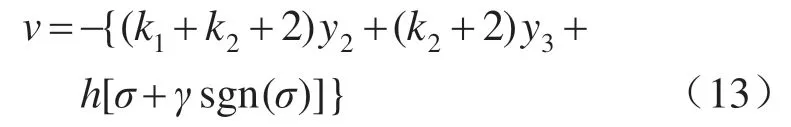
定义Lyapunov函数为V3=V2+σ2/2，则：

由于

因此

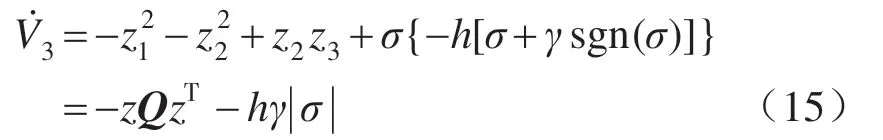
通过选取合适的h，k1，k2，γ值，可使|Q|＞0，从而保证矩阵Q正定，V3＜0，则系统满足了李雅普诺夫稳定性条件。

综上所述，风电机组变桨距系统BSMC如下式所示：

4 仿真结果及分析

本文基于额定功率为2 MW的变桨距风电机组模型，在Matlab/Simulink平台上将本文设计的控制器与SMC进行对比仿真。

本文研究的风力发电机组的主要参数：额定功率Pe=2 MW，额定风速ve=10 m/s，切入风速vin=3 m/s，切除风速vout=25 m/s，额定转速ωe=2.18 rad/s，空气密度ρ=1.25 kg/m3，执行机构时间常数Tβ=0.2 s，惯性环节时间常数Tω=0.05 s，风轮半径R=48 m，齿轮箱传动比γ1=30，风机转动惯量Jr=5.22×105kg·m2，发电机转动惯量Jg=58 kg·m2，极对数g=2，电网电压U1=220 V，定子绕组电阻r1=0.016 Ω，漏抗x1=0.22 Ω，转子绕组电阻r2=0.032 Ω，漏抗x2=0.14 Ω，浆距角变化范围-2°～97°。BSMC 参数选择为h=20，k1=10，k2=50，γ=1.5。

1）在额定风速附近对系统施加阵风（阶跃风）信号：假定在10 s 时，风速由10 m/s 变化为12 m/s，系统工况如图3所示。

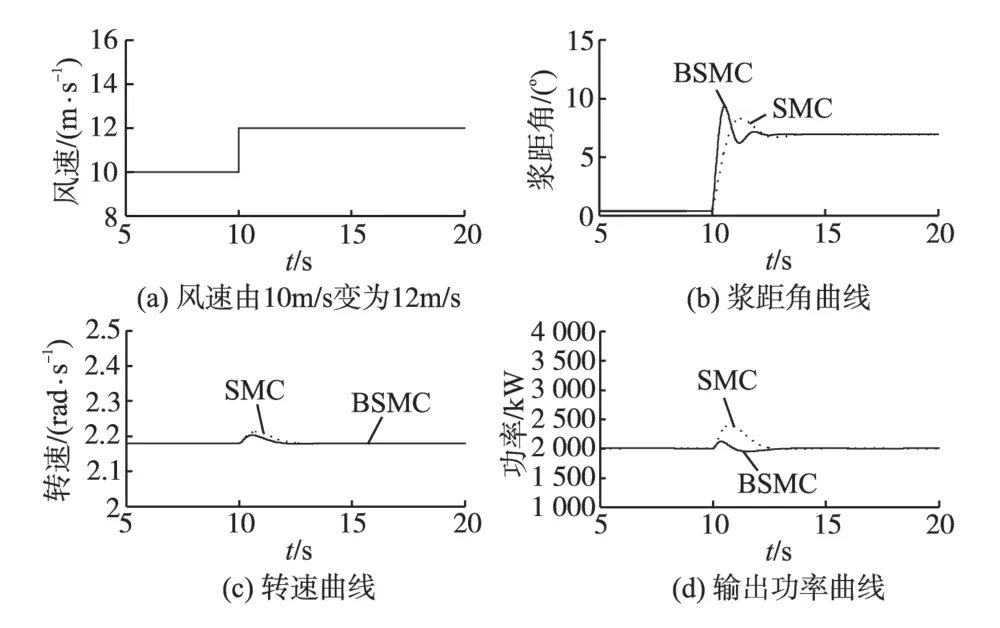
图3 阵风作用时的风电系统工况Fig.3 Wind power system conditions under step wind

由图3 可以看出，当风速由10 m/s 跃变为12 m/s时，与SMC相比较，采用BSMC时，系统响应速度快并且能在较短的时间内达到稳定状态。如图3d 可知，在BSMC 调节下，风力发电系统输出功率的超调量大大降低，调节时间也明显缩短，减小了对电网的冲击作用。

2）在额定风速附近对系统施加随机风信号，系统工况如图4所示。

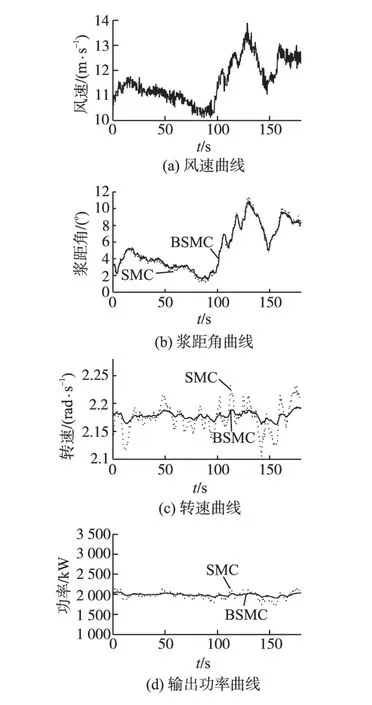
图4 随机风作用时的风电系统工况Fig.4 Wind power system conditions under random wind

由图4 可知，相比SMC，BSMC 能够快速响应随机变化的风速，对于维持风电机组输出功率具有更好的稳定性。由图4c 和图4d 可以看出BSMC 能使转速快速稳定，降低了输出功率幅值变化，较SMC 而言具有更好的控制性能。

5 结论

本文针对变桨距风力发电机组的系统特性及变桨距控制要求，采用EFBL 结合反推滑模控制的变桨距控制方案，应用于高风速下的恒功率控制。该方法避免了传统反推设计方法的计算复杂的问题，提高了变桨距控制系统的稳定性，使系统具有良好的动态性能。仿真结果表明，当风速突然发生变化时，BSMC 与SMC 相比，响应时间短，超调量小，具有良好的鲁棒性，能够更快地使系统稳定；在风速随机变化的情况下，可以较好地将转速限定在额定值附近从而平滑风电机组的功率输出，使之满足风电机组并网安全运行要求。

［1］徐浩，夏安俊，胡书举，等.大型风电机组变速变桨距协调控制技术研究［J］.电气传动，2012，42（6）：32-36.

［2］Van T L，Lee DC.Ouput Power Smoothening of Variablespeed Wind Turbine Systems by Pitch Angle Control［C］//IPEC.2012：166.

［3］王斌，吴焱，丁宏，等.变速变桨距风电机组的高风速变桨距控制［J］.电力自动化设备，2010，30（8）：81-83.

［4］孔屹刚，王志新.大型风电机组模糊滑模鲁棒控制器设计与仿真［J］.中国电机工程学报，2008，28（14）：136-141.

［5］韩旭杉，陈翡.基于模糊RBF 神经网络的风电机组变桨距控制［J］.电气传动，2011，41（2）：36-39.

［6］郭庆鼎，赵麟，郭洪澈.1 MW 变速变距风力发电机的滑模变结构鲁棒控制［J］.沈阳工业大学学报，2005，27（2）：171-174.

［7］高艳红.模糊滑模控制技术在风电机组中的应用研究［J］.电气制造，2011（9）：36-39.

［8］陈粟宋.风电机组模糊滑模变结构恒功率控制研究［J］.制造业自动化，2011，33（13）：16-20.

［9］王坚浩，胡剑波.不确定非线性系统的自适应反推高阶终端滑模控制［J］.控制与决策，2012，27（3）：413-418.

［10］冯晓艳，常国祥.永磁同步电动机反推控制［J］.自动化仪表，2010，31（6）：27-29.

［11］Hui Z，Guo-bao Z，Shu-min F.Enhanced Model Reference Adaptive Backstepping Control of Permanent Magnet Synchronous Generator Equipped Wind Energy Conversion System with Stator Parameters Varying［C］//Control and Decision Conference（CCDC），2011 Chinese.IEEE，2011：133-138.

［12］Seker M，Zergeroglu E，Tatlicioglu E.Robust Backstepping Control of Variable Speed Wind Turbines with Permanent Magnet Synchronous Generators［C］//Control Applications（CCA），2012 IEEE International Conference on.IEEE，2012：1068-1073.

［13］Wang G D，Wai R J，Liao Y.Design of Backstepping Power Control for Grid-side Converter of Voltage Source Converter-based High-voltage DC Wind Power Generation System［J］.IET Renewable Power Generation，2013，7（2）：118-133.

［14］Khemiri N，Khedher A，Mimouni M F.A Backstepping Control Strategy Applied to the Connected Hybrid Renewable Energy System Operated in MPPT［C］//Ecological Vehicles and Renewable Energies（EVER），2013：1-10.

［15］魏杰，邱晓燕，陈光堂，等.基于反馈线性化技术的直驱永磁同步风电机组低电压穿越研究［J］.可再生能源，2013，31（4）：41-44.