126kV真空断路器分离磁路式永磁操动机构

孙丽琼 王振兴 何塞楠 马立超 耿英三 刘志远

（电力设备电气绝缘国家重点实验室（西安交通大学） 西安 710049）

0 引言

真空断路器（Vacuum Circuit Breaker,VCB）因其优异的开断性能及可靠性，在中压领域获得了广泛的应用[1]，而SF6断路器在72kV 以上电压等级市场占主导地位[2]。为减少SF6气体所带来的强温室效应，研究和开发环境友好型输电等级真空开关具有重要意义[3]。

操动机构通过绝缘拉杆驱动真空灭弧室动触头运动，是真空断路器的关键部件。通过调节操动机构的动态特性曲线可以有效提高真空灭弧室的灭弧性能[4,5]。由于126kV 电压等级的输电系统对真空断路器有很高的要求，因此相应的操动机构应配合灭弧室达到最优的动态特性。

永磁操动机构（Permanent Magnetic Actuator,PMA）具有较强可控性，在分合闸位置，通过永磁体产生的永磁保持力将永磁机构可靠地保持在分合闸位置，在分合闸操作时，通过通电线圈产生的电磁力驱动动触头运动，从而达到关合或开断线路的目的。永磁机构一般分为单稳态机构和双稳态机构两种。但是，传统的永磁机构由于动作速度较低，目前报导仅限于较小开距（8～22mm）的中压（3.6～40.5kV）真空断路器中。

为了提高永磁机构的速度特性，国内外的研究者开展了大量的研究工作[6-10]。Lequesne B 为满足速度要求，提出了一种大开距下双弹簧螺线管结构[6]。R.Jong-Suk 等人提出了一种分离磁路的永磁操动机构以提高线圈工作效率[7]，但未实现磁路完全分离，分合闸保持或分合闸线圈通电时磁路会存在干扰。Cai Z.Y.等人尝试通过在传统双稳态永磁机构结构形式下，引入辅助线圈方式提高速度特性[8]。Kang 等人采用三连杆传动机构提高永磁机构速度特性[9]。Wang Z.X.等人采用分合闸线圈同时通电方式提高机构分闸速度特性[10]。但是，126kV 真空断路器的开距（约80mm）远高于中压真空断路器（＜30mm），而且126kV 真空断路器对动触头运动速度较高，要求分闸时动静触头在分开后 6～7ms 内开距达到18～20mm（对应分闸速度约2.5～3.3m/s），在12～13ms时开距达到36～40mm（对应分闸速度约2.7～3.3m/s）。因此要满足126kV 真空断路器的速度特性具有很大的难度。

本文的研究目标是提出一种分离磁路永磁操动机构以满足126kV 真空断路器速度特性要求。该永磁机构为双稳态结构形式，具有独立的永磁保持磁路和电磁驱动磁路。本文采用数值仿真方法计算了永磁机构的静态及动态特性，并根据计算结果制作了样机。样机的实验结果与仿真结果具有较好的一致性，并证明了本设计的可行性。

1 分离磁路永磁机构的结构及工作原理

传统永磁机构结构原理如图1所示。永磁体安置于静铁心中，永磁体产生的磁力线与线圈产生的磁力线共用磁路，这样的设计可以减小机构的体积。但是，由于它们共用磁路，在分闸操作起始阶段，永磁体产生的磁力会部分抵消线圈的电磁力，造成刚分速度难以提高。同时，线圈产生的电磁力既通过动铁心的上端面（见磁力线Ⅱ），也通过动铁心的下端面（见磁力线Ⅰ），造成线圈产生的电磁力一个拉动铁心运动，另一个阻碍铁心运动，降低线圈的工作效率。

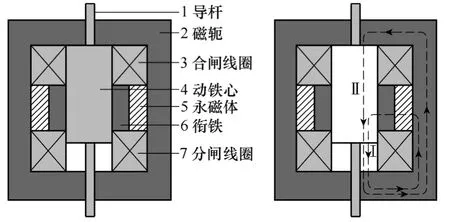
图1 传统永磁机构原理图Fig.1 Schematic of conventional PMA

本文提出的新型永磁机构采用轴对称结构，具有独立的驱动部分和保持部分，结构原理如图2所示，通过不导磁垫片7 将保持部分和驱动部分磁路进行隔离；同时，磁轭部分通过不导磁垫片12 将分闸和合闸过程的磁路进行隔离。

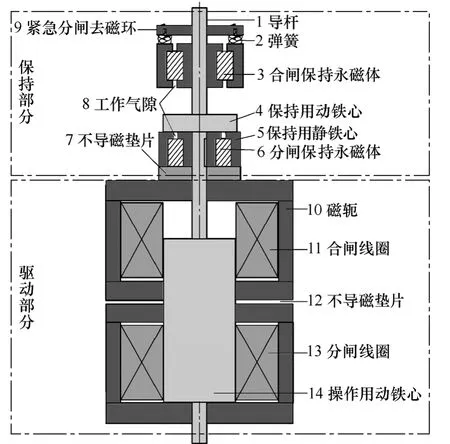
图2 分离磁路永磁机构原理图Fig.2 Schematic of separated magnetic PMA

当真空断路器处于分闸或合闸位置时，保持静铁心中的永磁体提供磁力即保持动铁心可靠保持在分/合闸位置。当断路器需要合/分闸操作时，电磁操动部分给合/分闸线圈通电，产生的电磁力驱动动铁心与保持动铁心一起运动，一旦保持动铁心与保持静铁心间气隙的大小超过静铁心中开槽所开气隙的宽度，则永磁体的磁力线会通过铁心中的气隙形成回路。这能快速降低保持动铁心所受的保持力，同时也降低了分、合闸初始阶段的反力，可以有效提供刚分速度。同时，由于合闸线圈和分闸线圈之间存在用非铁磁材料填充的气隙，可以保证磁力线只通过动铁心的上端面或下端面，克服了传统机构在动铁心的上、下端面均存在两个磁力线回路问题，因此能有效提高线圈的工作效率。

此外，设计中考虑了紧急分闸的需要。当紧急情况发生时，按下紧急分闸去磁环9 可以有效降低合闸保持力，帮助实现手动分闸，解决了传统永磁机构手动分闸困难的问题。

2 仿真方法

永磁机构特性仿真包含静态特性仿真和动态特性仿真。永磁机构静态特性分析是永磁机构结构设计的理论依据，同时也是动态特性分析的基础。本文采用Ansoft 有限元电磁仿真软件完成静态特性计算，分析了各参数对永磁机构电磁场的影响，从而选择工作性能最佳的参数，完成了永磁机构的结构设计。

永磁机构的运动过程包含了电路、磁场和机械运动等多个物理过程。永磁机构运动过程是电磁和机械综合的过渡过程决定的，它在电路上必须遵循电压平衡方程，在运动上遵循达朗贝尔方程，在磁场上遵循麦克斯韦方程，通过对这些动态方程的耦合求解，如式（1）所示，得到机构的动态特性[11,12]。

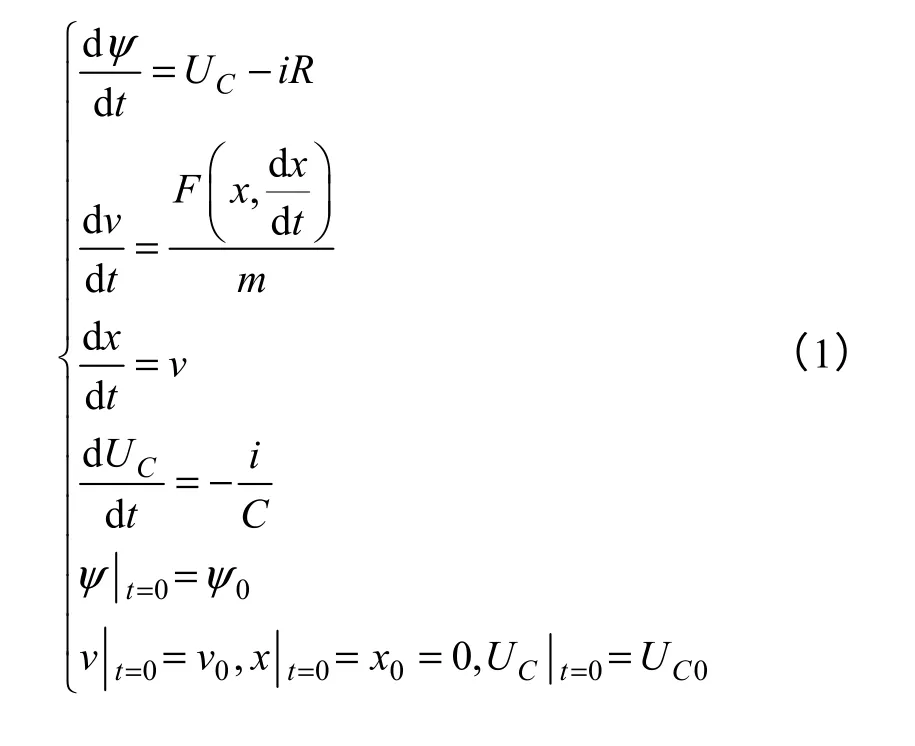
式中，ψ是永磁机构线圈产生的磁链；UC是放电电容器两端的电压；R是线圈电阻；i是线圈电流；v是运动部分的运动速度；F是电磁力；m是运动部分质量；x是运动部分的位移；C是电容器的容量。

为求解机构运动特性，首先，借助Ansoft 有限元分析软件辅助设计，建立机构静态特性计算的仿真模型，得到永磁机构动铁心在不同位置和不同线圈电流下所对应的电磁力和磁链数据，建立的数据网格。

然后，在Adams 软件中建立动态仿真模型，如图3所示。模型中包含真空灭弧室、永磁机构及触头簧。触头簧将动触头和永磁机构连接在一起，并且仅在动触头与静触头接触时才起作用。在合闸过程中，触头簧起阻力作用；在分闸过程中，触头簧起助力作用。

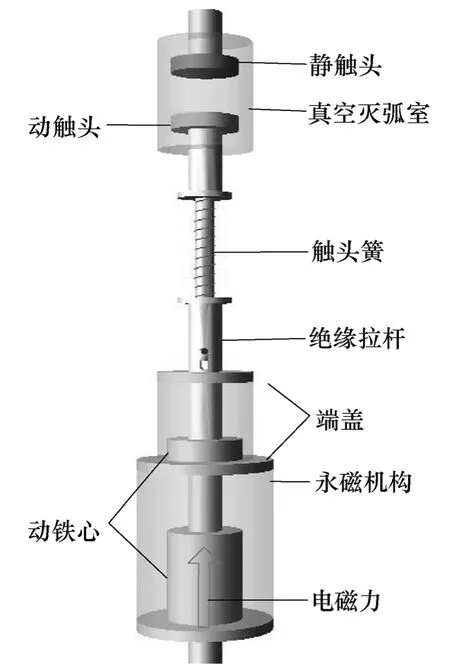
图3 126kV 真空断路器动态仿真模型Fig.3 Simulation model of 126kV VCB

动态系统模型中的运动是依靠永磁机构提供的电磁力驱动的，通过永磁机构静态特性求解得到的动铁心在不同位置和不同线圈电流下所对应的电磁力和磁链数据，F=f(i,x)、ψ=ψ(i,x)，在Fortran编译器中编写求解程序，通过Runge-Kutta 求解偏微分方程组（1），计算电压UC、磁链ψ值；应用二元二次插值法，根据气隙x、磁链ψ查表插值求出电磁力F和电流i值。利用Adams 软件的用户自定义功能将求解程序导入Adams 模型中，仿真中通过调用电磁力求解程序为模型加载力约束，电磁力驱动模型运动部件不断改变状态，从而完成整个运动过程仿真。

3 仿真结果

3.1 静态特性

永磁机构在分闸位置和合闸位置的磁力线分布如图4所示。因为在机构设计时将保持部分和驱动部分磁路进行了完全分离，因此，在仿真中，将保持部分和驱动部分作为独立部分进行考虑。分离磁路设计方法对永磁体和线圈参数的设计更灵活。

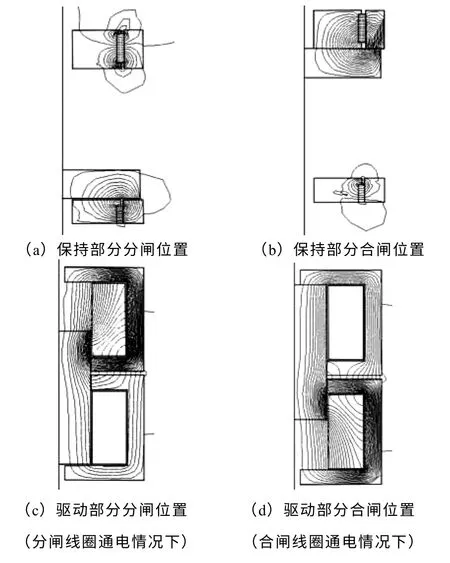
图4 永磁机构磁力线分布Fig.4 Flux distribution of PMA

永磁体作用下机构的静态吸力随机构行程的变化关系如图5所示。从图中可以看出，机构分闸保持力约为2 000N，合闸保持力为7 300N。从永磁体的吸力特性曲线还可以看出当保持动铁心离开分、合闸位置时，永磁体的磁力随气隙的变化急剧下降，也就是说，一旦动铁心开始运动，保持力对动铁心运动的阻碍将迅速减小，在几个毫米内几乎不再起作用。因此，动铁心初始运动速度将被提高。

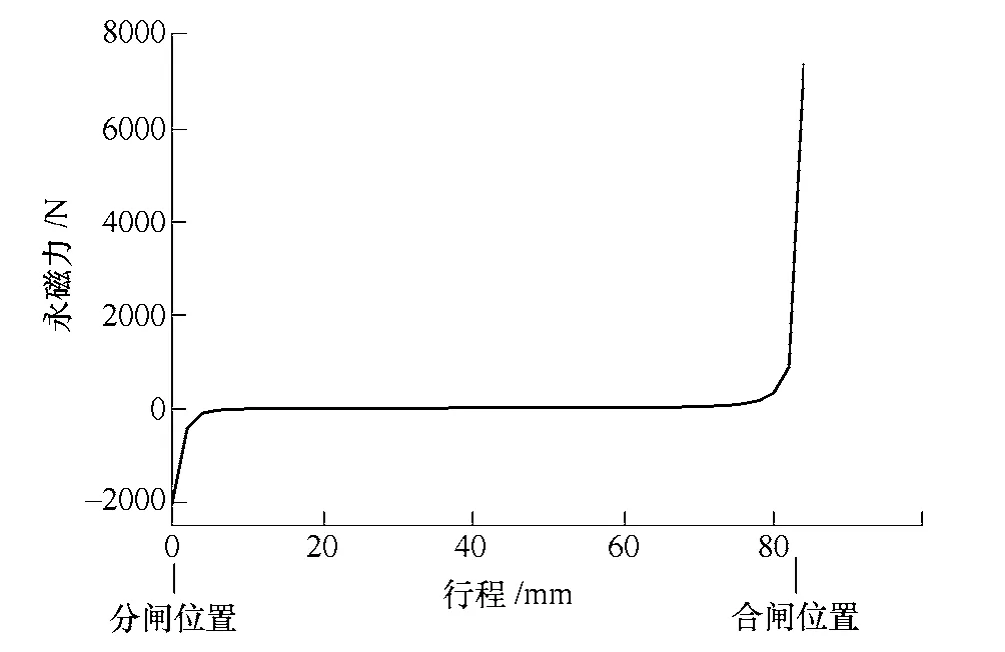
图5 永磁体作用下静态吸力随机构行程的变化Fig.5 Permanent magnetic force vs.stroke

3.2 动态特性

126kV 真空断路器仿真参数见表1。

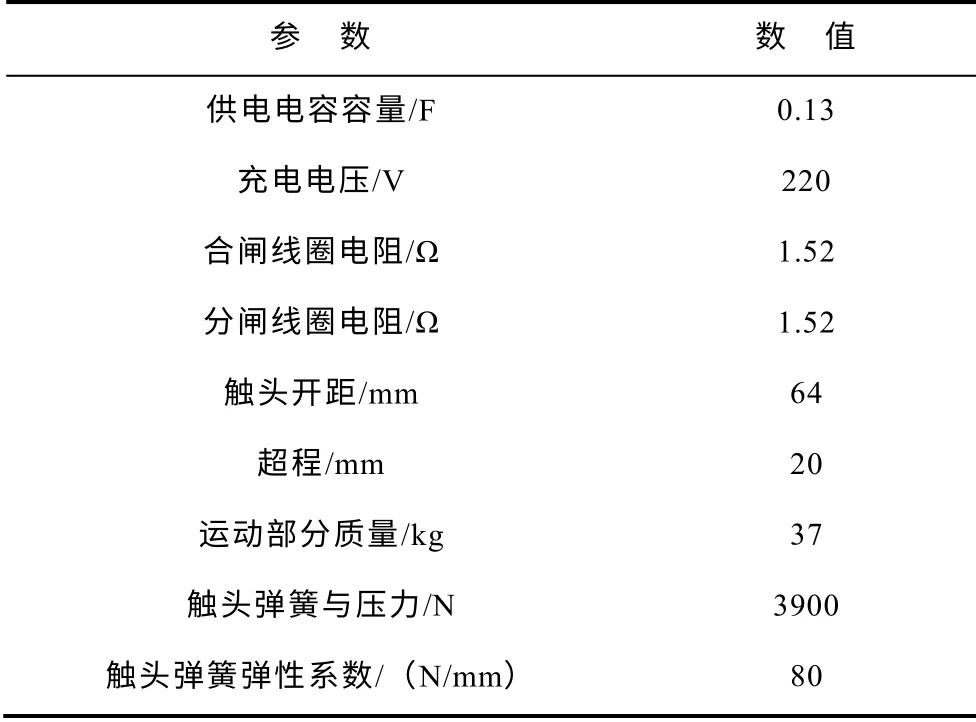
表1 仿真参数Tab.1 Simulation parameters

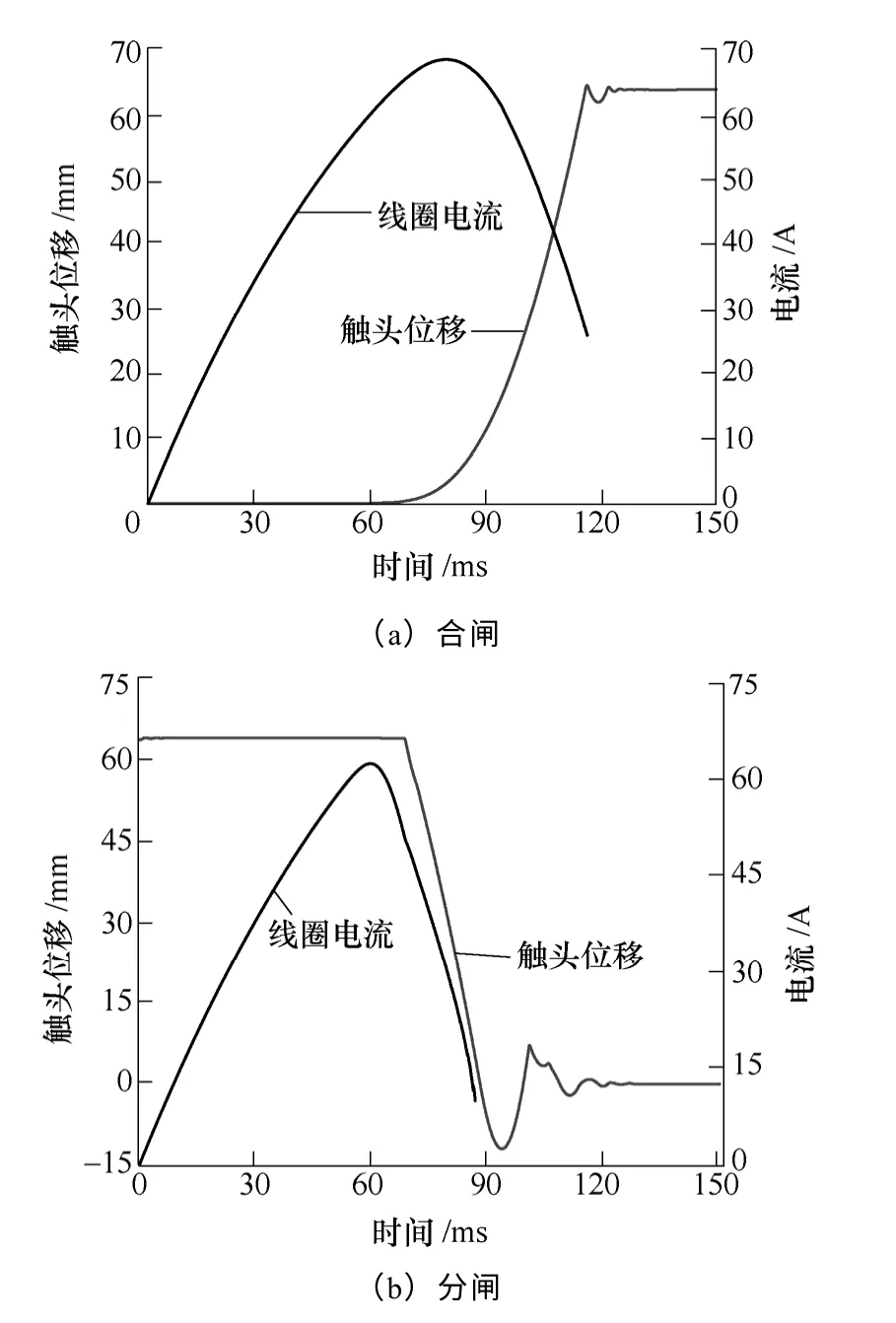
图6 合分闸过程的动触头位移及线圈电流曲线Fig.6 Displacement of movable contact and coil current curves during a closing and opening operation

图6a 给出了合闸过程中的动触头位移曲线及线圈电流曲线，从曲线可以看出，动触头平均合闸速度为2.0m/s（刚合前20mm 平均值）。而126kV真空断路器对此速度的要求为1.5m/s。从电流曲线可以看出，线圈通电后，电流开始指数上升，到达峰值后，动触头开始运动，电流随之下降。线圈电流的峰值时为82A 左右。

分闸过程中的动触头位移曲线及线圈电流曲线如图6b 所示。从图中的分闸曲线可以看出，动触头的刚分速度为2.8m/s（刚分点后6ms 平均值），平均分闸速度为3.0m/s（刚分点后12ms 平均值），满足126kV 真空断路器速度要求。在分闸过程中电流到达峰值时触头还没有开始运动，这是因为电流达到峰值时动铁心即开始运动，然而，动触头要等触头簧释放完超程后才开始运动。线圈电流的峰值为70A 左右。

3.3 供电电源影响

采用电容器组供电的方式作为励磁电路，选择不同的电容器充电电压和容量，对新机构进行动态特性计算。线圈电阻R=1.52Ω，线圈的通电时间都为150ms，计算结果见表2 和表3，表中UC0为电容充电初始电压，UC为动作结束后电容电压，ΔU为电容压降，C为供电电容容量，t1为从线圈通电到永磁机构动铁心开始动作的时间，t2为机构动作结束的时间，Δt=t2−t1为机构整个运动过程的时间，v分为刚分点后12ms 平均值。

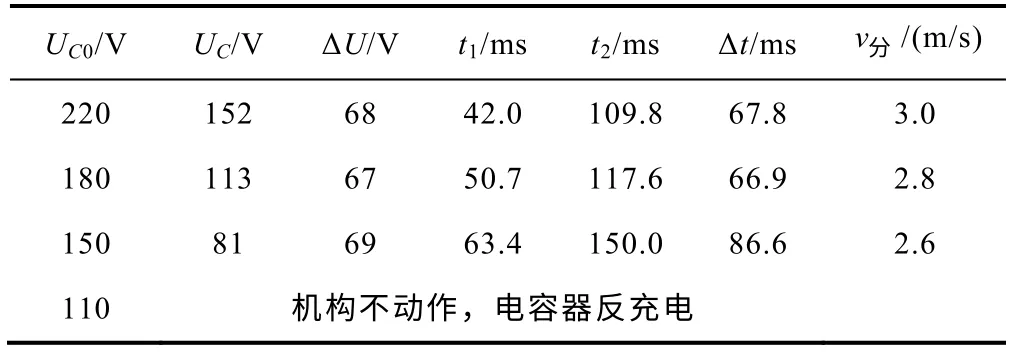
表2 电容器电压对动态性能的影响（C=0.13F）Tab.2 The relationship between dynamic performance and capacitor voltage（C=0.13F）

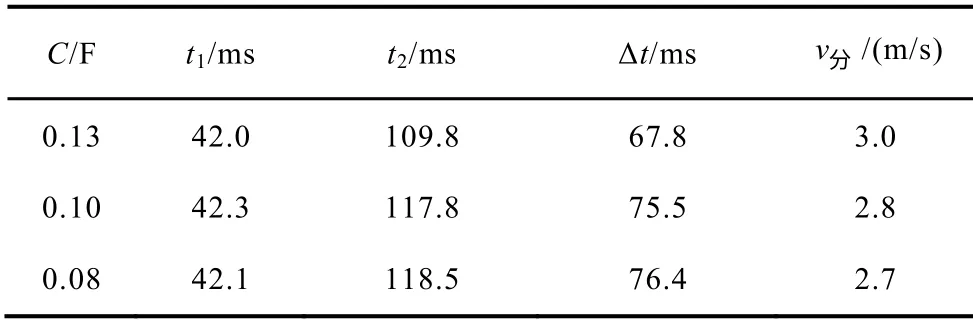
表3 电容器容量对动态性能的影响（UC0=220V，R=1.52Ω）Tab.3 The relationship between dynamic performance and the capacitor capacitance

从表中数据可以看出，在其他参数不变的情况下，电容充电电压越高，分闸速度越高；电容容量越大，分闸速度越高。

3.4 线圈参数影响

永磁机构中，励磁线圈的参数对机构动态性能的影响很大，在永磁机构其他结构参数及永磁体体积大小不变时，永磁机构的动作速度主要由线圈参数决定。选择不同的线圈线径和线圈匝数，就能获得不同的永磁机构动作和电流特性。表4 为不同的线圈参数对机构分闸特性的影响。表中IOmax为通过分闸线圈的峰值电流，t0为触头的启动时间，t为触头分闸时间，v分为机构的平均分闸速度。

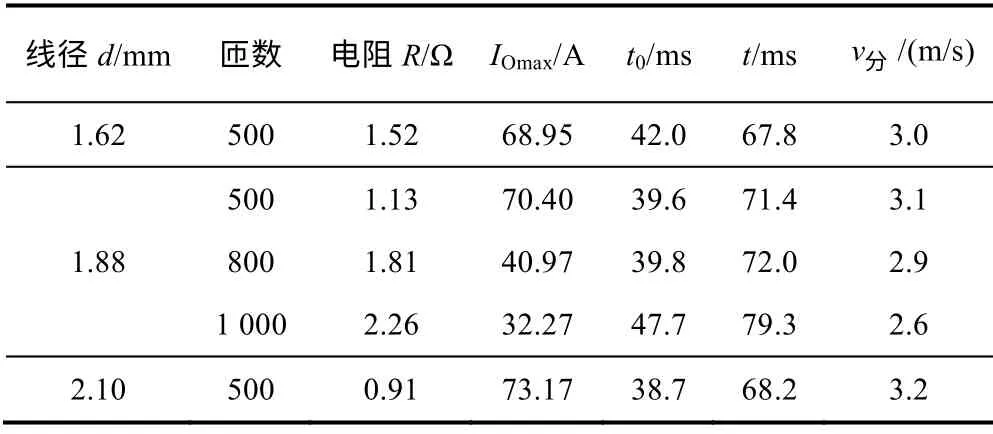
表4 线圈参数对机构分闸特性的影响（UC0=220V，C=0.13F）Tab.4 The relationship between dynamic performance and coil parameters

当线圈匝数一定时，线圈的线径越大，由于线圈电阻越小，从而分闸时线圈中流过的电流越大，分闸的时间越短，速度越快。而当线圈线径保持不变，线圈匝数越多，线圈电阻越大，线圈的电感也增大，使通过分闸线圈的电流增长变缓，电流峰值减小，分闸的时间变长，分闸速度降低。因此为提高分闸速度，一般采取减少线圈匝数、增大线圈线径的方法。但是如果选择较粗的导线线径，同时线圈匝数太少，线圈峰值电流较大，对控制系统的要求也越高，成本相应增加。而选择较细的导线，线圈电阻变大，虽然流过线圈中的电流变小，对控制系统电力电子元器件的参数要求也较低，但是以牺牲机构速度特性为代价的，可能会导致机构动态性能无法满足断路器要求。所以，要根据动态计算结果以及相关因素综合考虑，选择适当的导线匝数和线径，以达到机构的优化设计。根据励磁线圈参数仿真结果的比较分析，选择合闸线圈线径1.62mm，分闸线圈线径2.10mm。分、合闸线圈匝数均为500 匝。

4 实验装置及实验结果

126kV 真空断路器永磁机构样机及动态性能测试系统如图7所示。永磁机构操作的供电电源为并联电容器组。电容参数为：250V，22 000μF。将6 个电容器并联起来，总容量为0.13F。电容充电模块输出100～240V 电压。

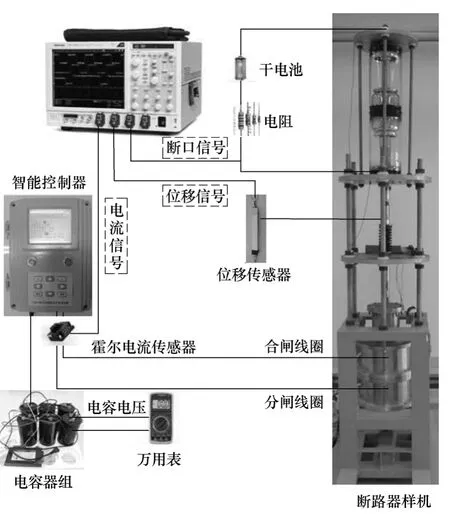
图7 126kV 真空断路器永磁机构样机及 动态性能测试系统Fig.7 Dynamic performance test system of PMA prototype for a 126kV VCB

为保障电网安全、可靠和经济的运行，智能控制器除具备基本分、合闸功能外，还需具备诸如运行参数测量、故障判断与处理及通信等功能。本文设计控制器总体框图如图8所示，由信号调理模块、通信模块、控制模块、计算模块、驱动模块和人机交互模块组成。信号采集模块集成了所需测量信号的传感器，传感器输出由信号调理模块处理后进行A-D 转换，输出数字信号，并对一些开关量通过光电耦合器进行隔离。由计算模块对采集到的数据进行分析处理，配合控制模块实现保护功能。通信模块通过以太网与上位机通信，同时将部分状态通过指示灯与显示屏进行显示。控制模块主要通过向IGBT 发出时间长度可控的导通信号而实现对分合闸操作的控制。本文选用 Altera 公司生产的Cyclone Ⅱ系列FPGA，DSP 选用TI 公司推出的TMS320C2000 系列。

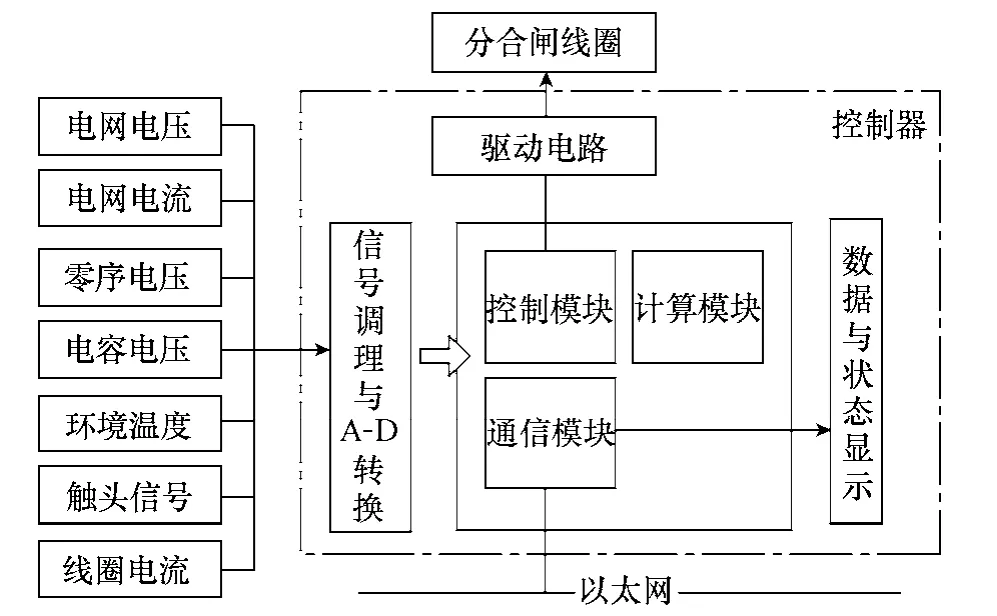
图8 智能控制器硬件框图Fig.8 The block diagram of intelligent controller

驱动部分原理图如图9所示。驱动电路的工作过程是通过IGBT 的导通将分、合闸线圈与相应电容接通，依靠分、合闸线圈流过电流产生的电磁力驱动铁心运动。同时，在IGBT 关断后提供续流回路，防止线圈能量无法释放产生的高电压损坏器件。

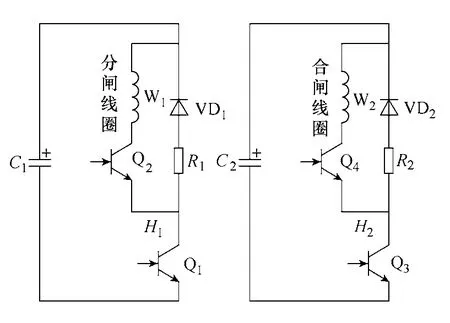
图9 驱动部分原理图Fig.9 The schematic of driving part

图10a 给出了动触头合闸位移曲线的实验及仿 真结果。实验结果与仿真结果基本一致，实验测得的平均合闸速度为1.8m/s（触头闭合前20mm平均值），此速度略高于要求的1.5m/s，可以通过调节控制回路将其降低。

动触头分闸位移曲线的实验及仿真结果如图10b 所示。实验测得的刚分速度为2.8m/s（刚分点后6ms 平均值），平均分闸速度为2.9m/s（刚分点后12ms 平均值）。

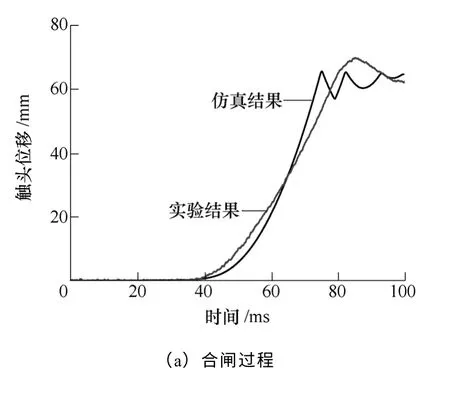
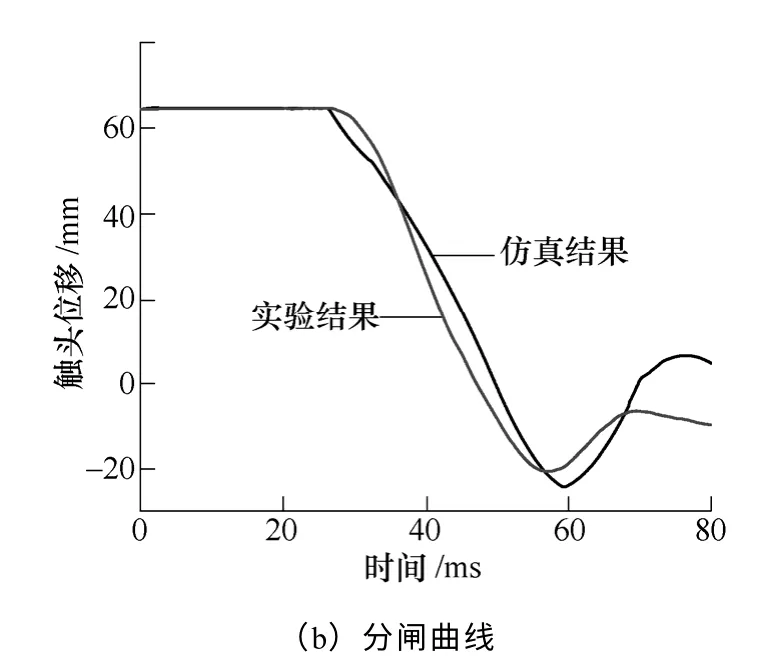
图10 动触头合闸、分闸位移曲线实验及仿真结果Fig.10 Displacement curves of the movable contact in a closing and opening operation compared with the calculated results

5 讨论

5.1 传统永磁机构与新型永磁机构静态特性比较

传统永磁机构和新型永磁机构静态特性仿真结果如图11所示。为保证两种机构性能的可比性，两个机构提供的合闸保持力（约7 300N）和分闸保持力（约2 000N）相同。但是，两个机构中永磁力随气隙的变化曲线却不同。从图中可以看出，当永磁机构接近合、分闸位置时，新型永磁机构提供的永磁力快速上升。这意味着永磁力对机构运动影响较传统机构更小，因为当动铁心离开合、分闸位置后，永磁保持力迅速减小。

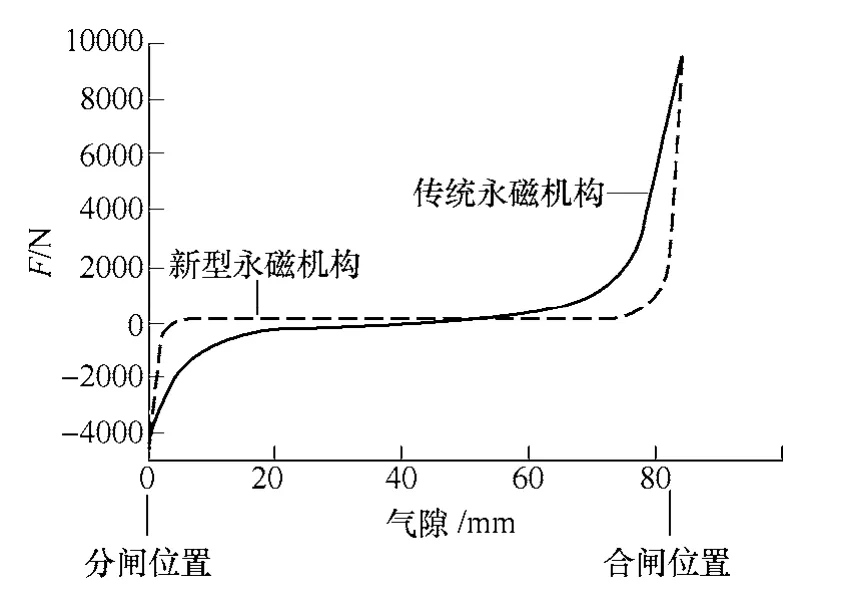
图11 传统永磁机构和新型永磁机构永磁力随气隙变化曲线（两种机构合闸保持力约为7 300N，分闸保持力约2 000N）Fig.11 The static forces vs.gaps of conventional PMA and proposed PMA(the holding force in the closing position is～7 300N,and～2 000N in the opening position)

5.2 传统永磁机构与新型永磁机构动态特性比较

在仿真得到两种机构静态特性数据的基础上，进一步通过仿真得到其动态特性。两种机构分合闸保持力几乎一致。仿真结果位移曲线和电流曲线分别如图12和图13所示。如图12所示，仿真得到传统永磁机构平均分闸速度为2.5m/s，而新型机构平均分闸速度为3.0m/s。从图13可以看出，新型机构的最大电流较传统机构大。更大的电流意味着线圈能在机构运动中能提供更大的电磁力，这也是新型机构能提高分闸速度的另一个原因。

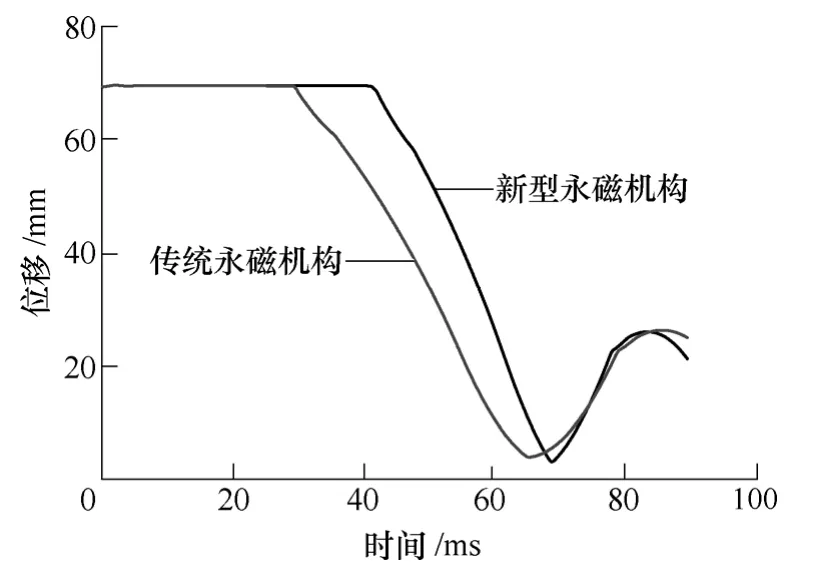
图12 传统机构和新型机构分闸动触头位移曲线Fig.12 The movable contact displacements of a conventional PMA and a proposed PMA during opening operations

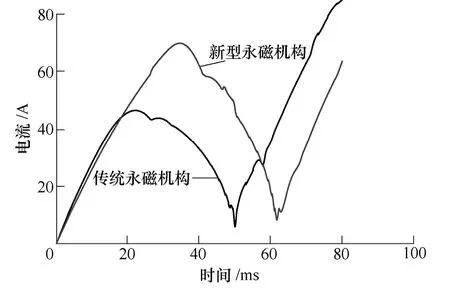
图13 传统永磁机构和新型永磁机构分闸线圈电流曲线Fig.13 The opening currents of a conventional PMA and a proposed PMA during opening operations

6 结论

本文提出了一种具有分离磁路的126kV 真空断路器永磁操动机构。该机构为双稳态、轴对称永磁机构，驱动部分、保持部分具有独立磁路。本文计算了本机构的静态特性及动态特性，并根据计算结果制作了样机。样机的合闸速度可达到1.8m/s（触头闭合前20mm 内平均速度），刚分速度为2.8m/s（触头分开后6ms 内平均速度），平均分闸速度为2.9m/s（触头分开后12ms 内平均速度）。此速度特性满足126kV 真空断路器的要求。同时对比传统永磁机构和新型分离磁路永磁机构静态特性及动态特性，新型机构较传统机构分闸速度更高，电流更大。

[1]Slade P G.The vacuum interrupter:theory,design,and application[M].London:CRC,2008.

[2]Yanabu S,Zaima E,Hasegawa T.Historical review of high voltage switchgear developments in the 20th century for power transmission and distribution system in Japan[J].IEEE Transactions on Power Delivery,2006,21(2):659-664.

[3]Liu Z Y,Wang J M,Xiu S X,et al.Development of high-voltage vacuum circuit breakers in China[J].IEEE Transactions on Plasma Science,2007,35(4):856-865.

[4]Kong G W,Liu Z Y,Wang D,et al.High-current vacuum arc:the relationship between anode phenomena and the average opening velocity of vacuum interrupter[J].IEEE Transactions on Plasma Science,2011,39(6):1370-1378.

[5]Sun L Q,Yu L,Liu Z Y,et al.An opening displacement curve characteristic determined by high-current anode phenomena of a vacuum interrupter[J].IEEE Trans- actions on Power Delivery,2013,28(4):2585-2593.

[6]Lequesne B.Fast-acting long-stroke bistable solenoids with moving permanent magnets[J].IEEE Transactions on Industry Applications,1990,26(5):848-856.

[7]Ro J S,Hong S K,Jung H K.Characteristic analysis and design of a novel permanent magnetic actuator for a vacuum circuit breaker[J].IET Electric Power Appli- cations,2013,7(2):87-96.

[8]Cai Z Y,Ma S H,Wang J M.An approach of improve permanent magnetic actuator of vacuum circuit breaker[C].International Symposium on Discharges and Electrical Insulation in Vacuum,2008,1:165- 168.

[9]Kang J H,Kwak S Y,Kim R E,et al.The optimal design and dynamic characteristics analysis of electric actuator(EMFA)for 170kV/50kA VCB based on three- link structure[C].International Symposium on Disch- arges and Electrical Insulation in Vacuum,2008,1:177-180.

[10]Wang Z X,Yan P,Geng Y S,et al.Simulation of an improved operating method for vacuum circuit breakers with permanent magnetic actuators[J].International Journal of Applied Electromagnetics and Mechanics,2010,33(3-4):1373-1381.