基于符号动力学的变压器内部故障检测

李 涛 陈巍家

（湖南大学信息科学与工程学院 长沙 410082）

0 引言

在电力系统中，变压器作为电力能源变送和分配的主要枢纽，其安全性和稳定性对电网稳定运行至关重要。因此，对变压器的检修是必不可少的。

目前，广泛使用的变压器在线检测方法主要有：油中气体分析法（Dissolved Gas Analysis，DGA）和糖醛分析法。DGA 可以知道变压器内部的故障程度，但是并不能发现故障的具体位置，同时灵敏度不高，故障发现相对滞后[1-3]。糖醛分析法检测绝缘层老化情况，对使用了一定年限的变压器检测效果较好，但是对于新安装的变压器检测效果不佳[4,5]。此外还可以直接通过红外线来监测变压器的内部的温度，或者直接在变压器内部安装摄像头进行视频监控，利用图像识别技术发现变压器内部机械故障[6]。近年来，国内外学者引入模糊理论、灰色理论等方法将以上提到的各种在线监测实验和历史数据、运工状况信息进行综合尝试着建立一个系统的变压器状态评估体系[7-9]。本文提出的基于符号动力学的在线检测方法可以作为该体系考量的重要指标之一。

本文提出了基于符号动力学的对变压器内部早期故障进行检测并对变压器的运行状态进行评估的方法。首先通过仿真变压器的内部故障状态，获取故障状态下的电流数据运用符号动力学方法与同负载下正常电流数据对比，以验证有效性。文中使用符号动力学模型中的共同信号指标（Common Signal Index，CSI）来评估信号的畸变，同时，还将统计学方法柯尔莫戈洛夫-斯米尔洛夫检验（Kolmgorov- Smirnov，KS）加入对比进行辅助验证。目前常用的变压器仿真方法分为数学关系仿真和矩阵表达仿真。数学关系通过建立变压器的工作数学关系，实现数学函数来构建整个仿真模型[10]。矩阵表达仿真通过描述变压器各个绕组之间的物理量关系进行仿真，同时，矩阵仿真方法还可以仿真变压器所处的电网环境，因此该方法所考虑的环境因素变量较多[11]。为了较好地说明符号动力学的有效性，本文采取了数学关系仿真法，忽略了电网环境对变压器内部故障的影响。在完成仿真理论验证之后，本文将利用变压器内部故障的现场数据对符号动力学方法进行进一步验证。

1 变压器内部故障与仿真

1.1 变压器内部故障

常见的变压器内部电气故障包括匝地短路、相间短路、匝间短路和铁心故障。其中，匝间短路故障最为常见，因此本文将匝间故障作为仿真和实验的对象。本文的目标是利用符号动力学的方法对早期内部故障进行有效检测。

1.2 变压器数学模型

本文介绍一种以磁链作为中间变量联系电流和电压的变压器的数学模型[10]。

1.2.1 磁链方程

变压器每一个绕组的磁通由主磁通和漏磁通组成，可以用如下公式表示

式中，1lϕ和l2ϕ分别为绕组1 和2 的漏磁通；mϕ表示主磁通。

设绕组1 的匝数为N1，根据磁链的定义有

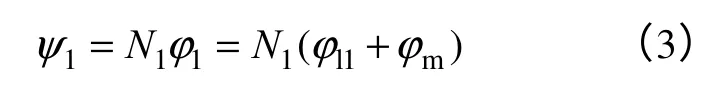
磁动势乘磁阻等于磁通，式（3）改写为

式中，绕组1 的磁动势为N1i1；其漏磁通磁路的磁阻为Rml1；主磁通磁路磁阻为Rmm。

同理，对于绕组2 的磁链有

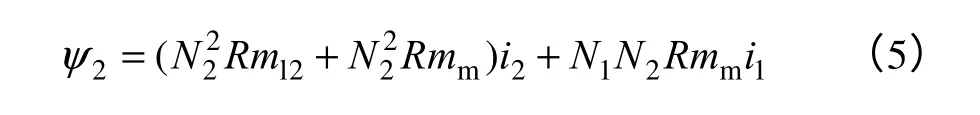
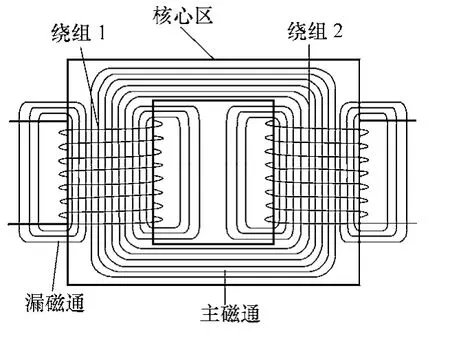
图1 变压器模型Fig.1 The model of transformer

根据磁链的定义，式（4）和式（5）可以改写为

式中，L11、L22分别为绕组1 和绕组2 的自感；L12为互感。

L11可以看成是绕组1 的漏电感和电流i1单独在绕组1 上起作用的电感的和。因此有

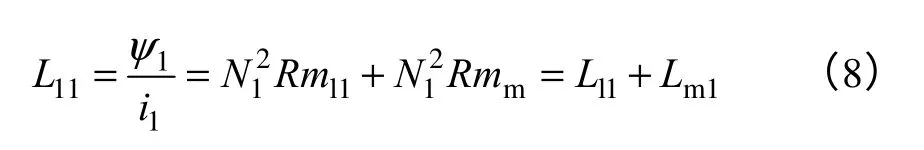
同理

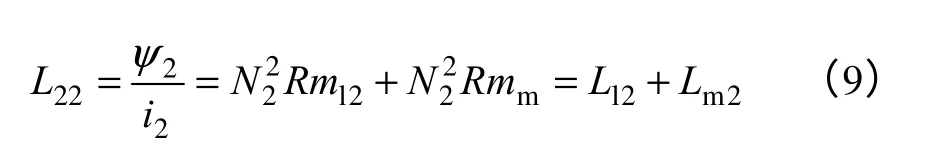
根据匝比有

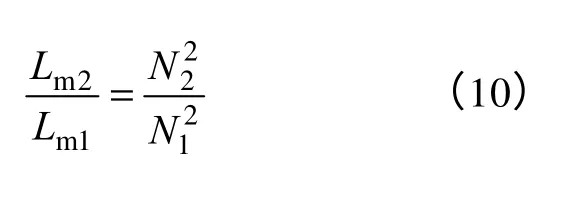
1.2.2 感应电压方程

根据感应电压的定义，在考虑匝数的情况下，磁链的变化率即为感应电压。利用式（5）的磁链表达式可以得到感应电压的表达式

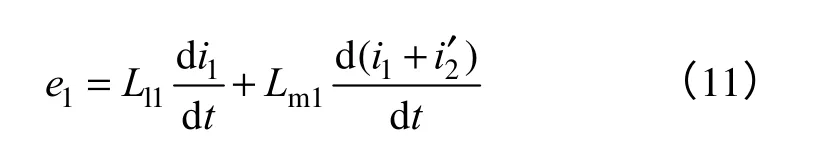
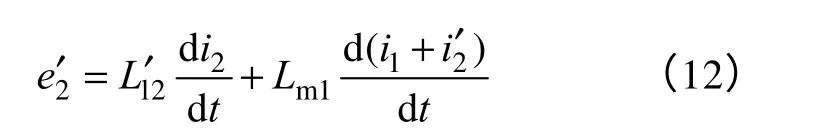
考虑绕组的阻抗压降，绕组端电压的电压公式为

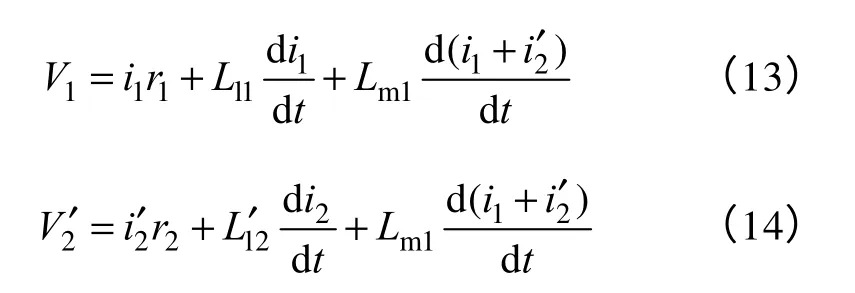
1.2.3 仿真模型

使用磁链作为中间变量表示电压，式（13）和式（14）可以表示为

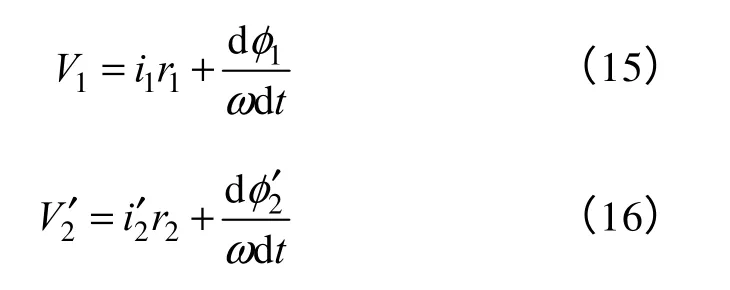
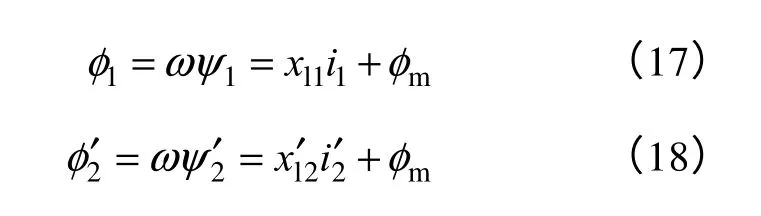
式中

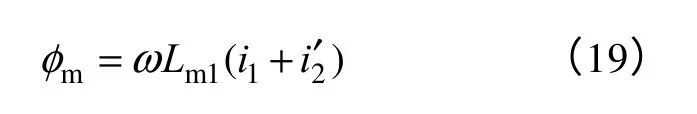
利用磁链表达式对式（17）和式（18）作变形得到

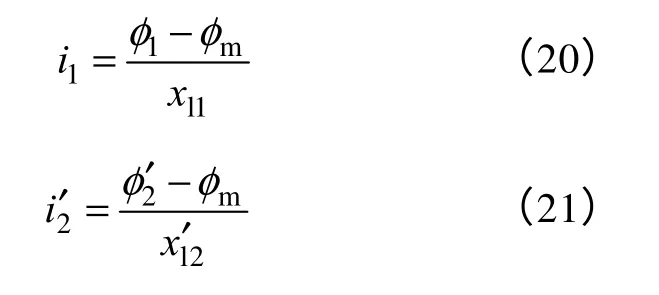
将式（20）和式（21）代入式（19）有

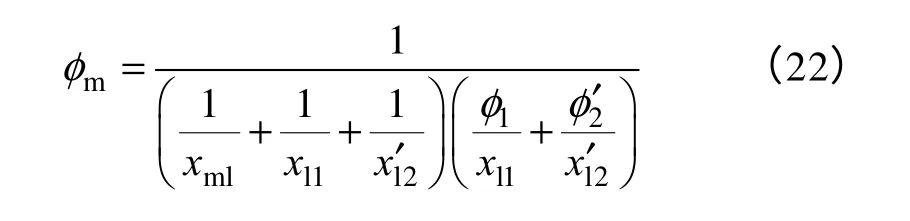
再用电流公式（20）和式（21）代入电压公式（15）和式（16）得到积分形式的电压和磁链的关系公式

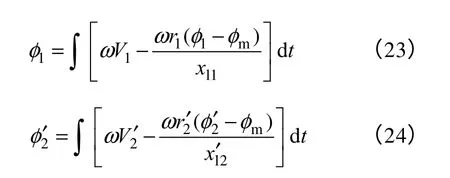
这样式（20）～式（24）就构成了由磁链、电压和电流描述的变压的仿真模型。在仿真的时候如果要考虑铁心饱和的情况，可以在式（22）中加入一项Δφ/xml，Δφ表示饱和磁通和当前磁通的差值，这样随着绕组磁通的增加，主磁通不会无限增加，模拟了铁心饱和的情况。

2 符号动力学技术

符号动力学起源于对动力系统的研究，但发展迅速，其研究领域已经不局限于动力系统。由于符号动力学自身的特点，其在数据的表示、传输和线性代数，生物医疗等方面都有很好的应用[12,13]。

在研究动力系统时符号动力学将系统状态取值空间进行划分，每一个划分表征系统的一个状态。对系统的观察结果是相空间中的一条轨道，用相应的符号代表系统状态之后，就获取了符号化表达。这是对信号的粗粒化描述，同时保留了鲁棒性和信号的特征。在故障检测中，变压器是非线性系统，正常和故障信号是变压器系统的两种不同状态，故障的发现可以认为是计算相空间中两个信号轨道之间偏离程度。

符号动力学的第一步工作是通过相空间划分将连续信号转化为符号序列。相空间的划分依赖于映射函数，最简单一种映射函数的是单峰映射，其形式为ωn+1=f(μ,ωn)，这里的μ为参数或者参数的组合[14]。相空间划分的目的是得到一个对原信号有最佳表达符号序列，因此可以依据信号的变化、最大熵或者分层的办法对相空间进行划分[15]。本文采取基于最大熵的相空间划分法，以保证符号化的序列最大限度地保留原信号的特征[15]。另外，在进行序列化之前，为了确保算法的速度，可以选择依据奈奎斯特抽样定理对原信号进行抽样，减少信号的采样点，以适应检测方法实时性的需求。

获取了系统在不同状态下的符号序列之后，就可以利用符号动力学来检测信号差异程度。在故障检测应用中，符号动力学方法基于如下基本理论：①在较短的时间段内，系统的行为可以看成是不变的；②如果系统发生故障，那么在一个较长的时间段内这个故障可以被观察到[16]。

在进一步阐释之前，先给出一些符号动力学定义[17]。词：符号序列中，连续的一个或几个符号的组合。字典：一个信号序列中，所有的可能出现的词的组合。频次：在这个字典中，某个词出现的次数。频率：在这个字典中，某个词出现的次数与字典中词数的比值。

2.1 构建字典

每次考虑符号序列中的一个词插入字典，词的长度从1 开始增长直到规定的最大词长Nmax。对于长度不足的词，多余的符号位置用0 代替。字典的最后一列附加每一个词对应的频率。图2展示了字典的形成和结构。字典的词数可以用式（2）计算。

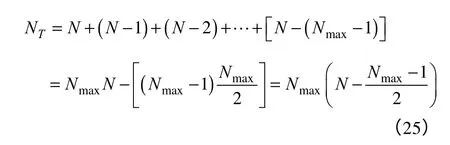
式中，N为序列中符号数。

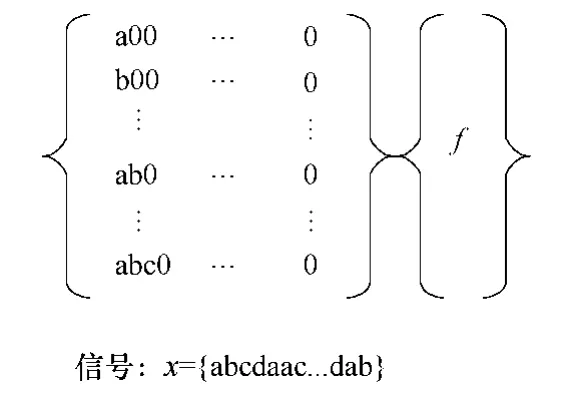
图2 字典的结构Fig.2 The structure of the dictionary

2.2 CSI 共同信号指标

共同信号指标是衡量两个信号差异程度的指标。待比较的两个信号经过序列化之后转换成字典，然后计算出字典中词的频率，CSI 是和词频有关的参考标量。符号动力学中有下列5 种CSI 可以使用。

式中，N为两个字典中都出现的词的总数；fxi、fyi为信号在各自的字典中第i个词的频率。

2.3 信号比较

在仿真中，通过对比健康和故障状态下的一次电流，可以确定在变压器所处的运行状态，比较过程如图3所示。为健康和故障状态下的一次电流符号序列数据分别构造两个独立的字典。

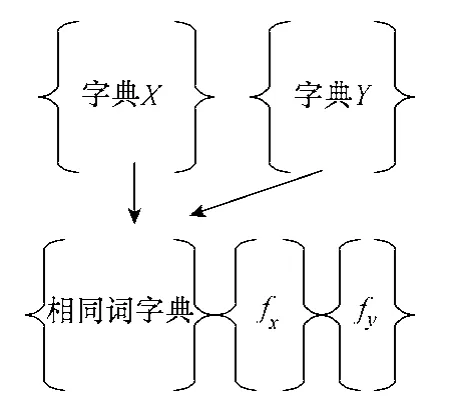
图3 信号的比较Fig.3 The comparison of signals

逐行对比两个字典选出相同的词构建新的共同词字典，将词在各自原字典中的频率分别附加在字典最后，再通过CSI 公式计算差异程度。

2.4 KS 测试

KS 检验也是用于检查两个信号相似程度的方法。它是一种统计学方法，已知两个信号序列的经验分布函数，可以利用KS 算法得出衡量这两个分布的差异的变量[18]。

已知容量为M和N的样本X1X2…XM，Y1Y2…YN，对于所有的采样点t，将两个信号的经验分布函数定义为

在KS 测试中检测两种假设：

H0:FM(t) 对于所有的t都等于GN(t)

H1:至少有一个t使得 :FM(t) 不等于GN(t)

定义k为M和N的最大公约数。那么KS 双边双样本检验统计量J可以被定义为

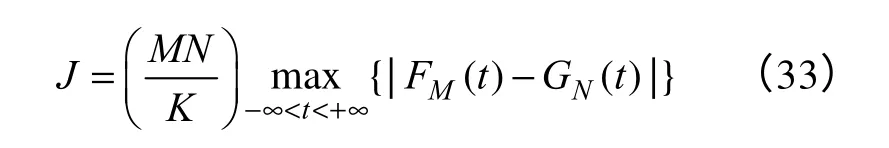
将X和Y归并且按升序排列，用Z(i)表示其中的数据，那么J可以被写成

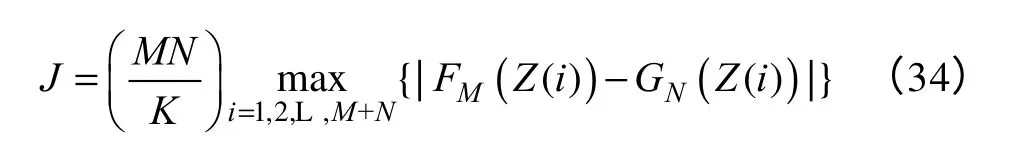
当样本很大的时候，上面的双边双样本统计量J可以被写成

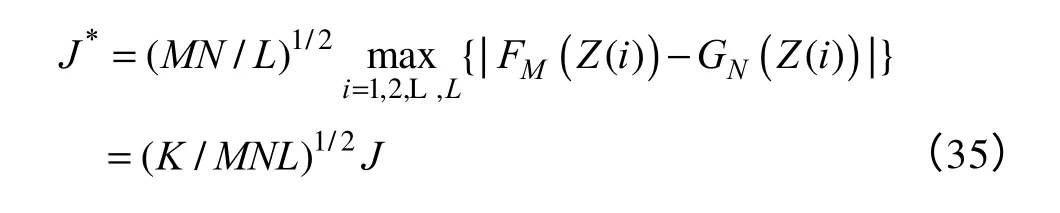
式中，L=M+N。

对于大样本定义概率[18]

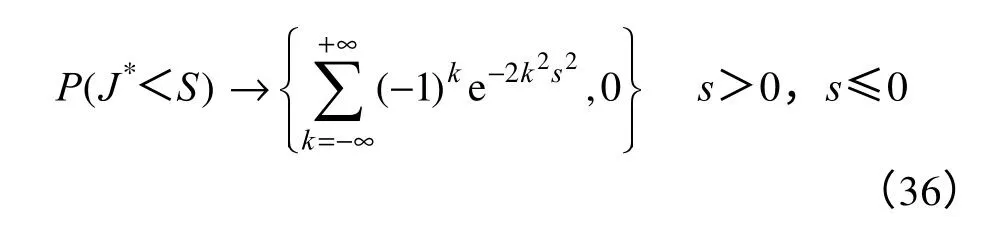
定义Q函数为[18]

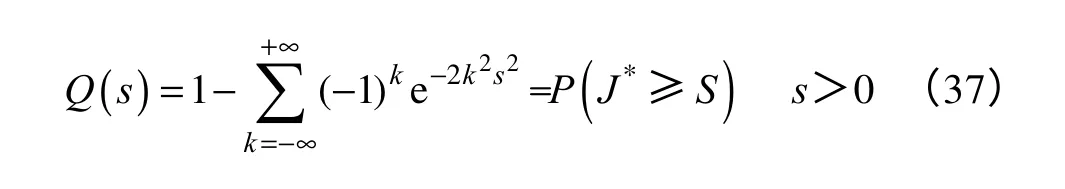
这样计算得到检验统计量J*即可代入Q函数求解概率，式（36）表示以什么样的概率拒绝假设H0。

3 实验及结果分析

为了检查符号动力学的有效性，本文分别在仿真数据和现场故障数据上做了实验。在正式实验之前，首先对5 个CSI 公式和MEP 算法进行测试。

3.1 CSI 测试

通过一些简单的序列数据来测试CSI，并且合理选择算法中所用参数的数值。合理的CSI 应该满足随着信号之间的差异程度变大，CSI 呈正相关或者反相关。

简便起见，在CSI 测试中，本文使用了标准正弦信号和相位从 0°～90°移动的正弦信号进行对比，对比结果如图4所示。由图4可知，CIS1和CSI5都整体随着信号相位差异增大而减小，而CSI1的起始点为0.5，故本文接下来的测试将选择CSI1作为信号差异度指标。

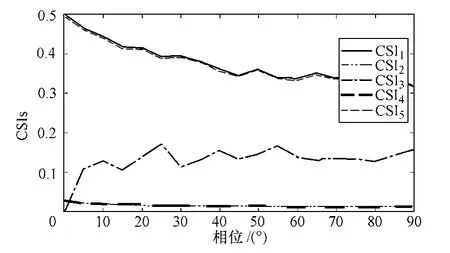
图4 CSI 的比较Fig.4 The comparison of CSIs

图5给出了信号长度变化对CSI 的影响效果。由图5可知，周期数的增长整体上会导致CSI 的变化速度减慢，影响区分能力。这是由于，周期变长会导致词典中词数的变多，从而每个词的分数频率变小，最终将使得计算结果变小，整体上提高了两个信号的相似度。因此，不需要太多的信号数据即可对故障进行有效检测。

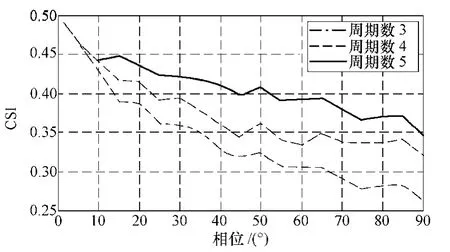
图5 信号长度的效果Fig.5 The effect of the length of the signal

图6显示增加字典字长，信号的粗粒化程度下降，将增加对信号的区分能力，但同时增加计算时间。因此本文取字长等于4。

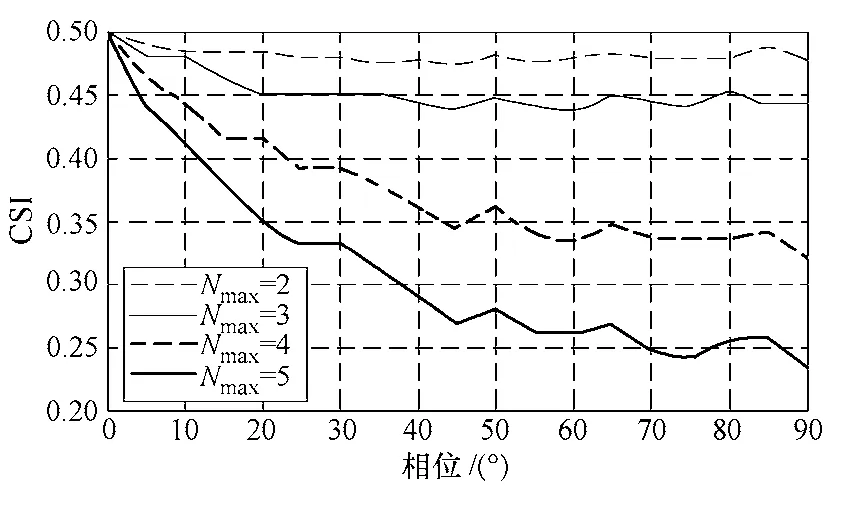
图6 字长的效果Fig.6 The effect of the word length

3.2 基于最大熵的相空间划分法

当对相空间进行划分的时候，直觉上可以知道，在信号变化较剧烈的地方应该给予更多的符号进行表达，而在信号单调变化的地方可以适当减少划分次数，因此基于最大熵的划分与传统的均匀划分法不同，在划分数（即符号数）一定的情况下 MEP可以确保符号化序列保留原信号最大的信息量，即最大熵。算法主要流程如下：将原始序列按数值升序排序，N为序列长度，K为划分数，每连续的个（不大于N/K的最大整数）信号点作为一个区域对信号进行序列化，通过计算每一种划分的熵，选择出最佳的相空间划分。具体过程见参考文献[15]。

MEP 算法中，门限参数e决定最终相空间的划分数目，门限取值和相空间数目呈反相关关系。

图7所示为门限参数e对CSI 的影响效果。由图7可知，随着门限参数取值的减小对信号的区分能力逐渐增强，但同时需要更多的算法执行时间。

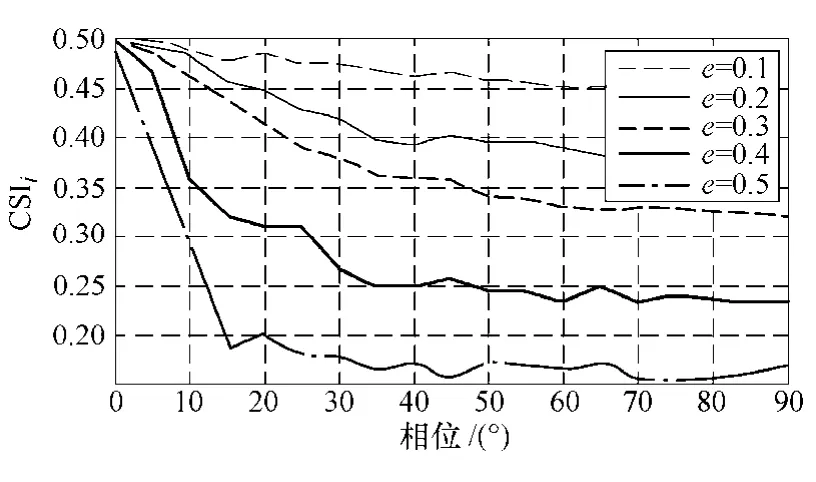
图7 参数e的效果Fig.7 The effect of the parametere

因此，需要在准确度和计算时间上进行取舍。为了达到区分的效果本文取门限参数e=0.2。

综上所述，在后面的仿真测试中，本文将取最大字长等于4，门限参数e=0.2，进一步做下面的测试。

3.3 仿真测试

利用前面介绍的仿真模型，本文实现了对变压器匝间故障的仿真，仿真变压器的参数如下：

利用仿真模型得到的数据，本文进行了简单的验证，在负载一定的情况下，仿真了变压器内部故障匝数不同的8 种情况（故障情况模拟阻抗下降为原来的70%），计算参数选取如上节所述，在计算之前，根据奈奎斯特定理对信号进行了抽样降低数据量以保证计算速度，得到表1 中的结果。

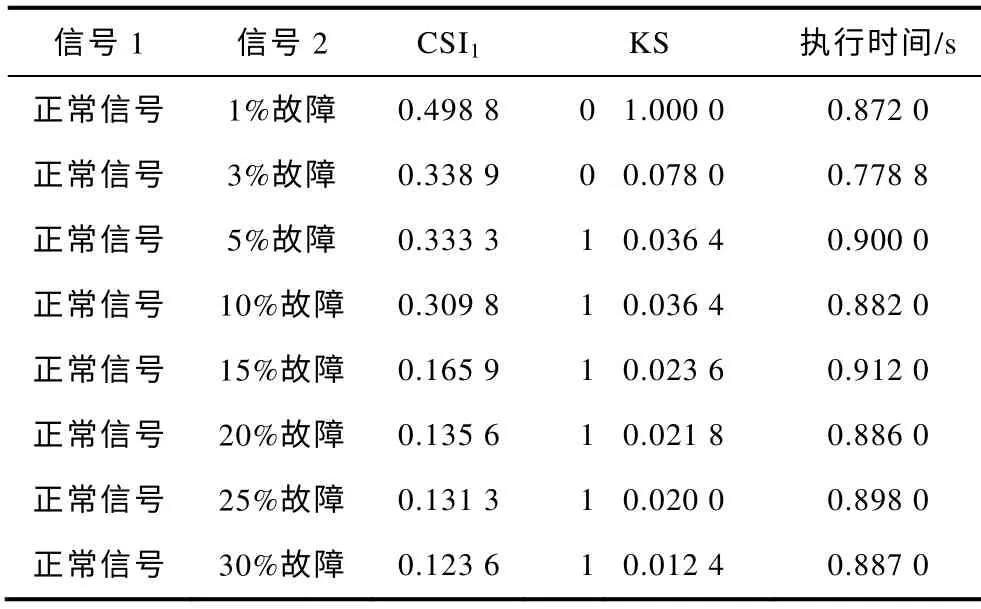
表1 变压器匝间故障测试Tab.1 Test on the transformer internal fault data

由表1 可知，符号动力学可以检测出信号差异，且随着故障程度加深，信号的差异增大，CSI 数值逐渐减小。KS 检验也体现了随着信号差异程度变大，两个信号是相同分布的概率逐渐降低。

图8为变压器匝间故障的测试结果。整个算法的时间复杂度为O(n2)[15,17]。符号动力学算法执行的平均时间为0.877 0s，可以满足实时检测的要求。

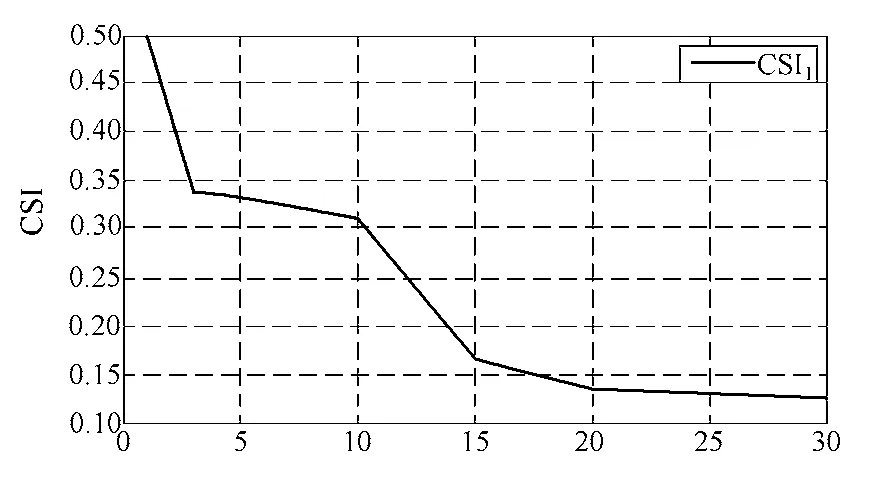
图8 变压器匝间故障测试Fig.8 Test on the transformer internal fault data

需要补充的是，这里只对变压器的内部匝间故障应用了符号动力学验证。但因为其他4 个内部故障的本质都是内部绝缘系统的问题，故表现在电流方程（方程中各个字母代表的物理量如第1 节所述）中都是一个随着时间缓慢减小的阻抗r1+jxl1[16]。因此 MEP相空间划分结合CSI 的判断方法适用于其他的变压器内部故障。

3.4 现场测试

本文取得了某变电站2012年3月1日11时35分变压器区内故障的一次电流数据。在电流数据上用符号动力学方法进行分析，其结果见表2。

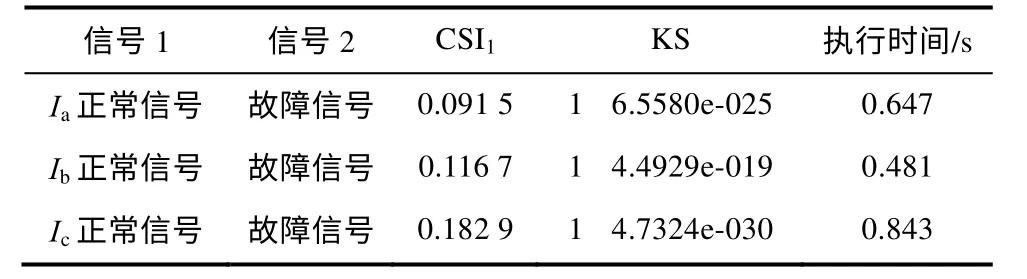
表2 变压器现场数据测试Tab.2 Test on the field data of transformer

由于收集的数据表示变压器内部已经发生短路，故计算得到的CSI 数值偏小，这样的CSI 数值说明此时变压器内部已经发生较严重的故障，这与实际情况吻合。实验表明在目标信号较大的变化范围中（从正常到短路），符号动力学算法的运算时间稳定，能够判断出信号差异程度，同时结合算法本身的鲁棒性，可以认为该方法具有一定的可靠性。根据上面的实验计算，用本文使用的参数和变压器类型，可以简单地设定状态，当CSI＜0.3时认为变压器需要检修；0.3＜CSI＜0.4时处于警戒状态；CSI＞0.4 说明变压器还处在较健康的状态。

4 结论

本文提出了一种新的基于符号动力学的变压器在线故障检测方法。在信号序列化过程中为了使粗粒化符号序列可以最大限度地保留原信号的特征，本文引入了MEP 算法。在信号分析时使用CSI 作为故障程度的数值标志，并根据CSI 为变压器设置了健康、警戒、需要检修三种状态。结果分析中结合KS 检验对比验证了符号动力学方法的有效性。实验结果表明，针对特定变压器合理选取参数，符号动力学可以有效地发现变压器的早期内部故障，为状态检修提供了依据。此外，建立符号动力学检测系统相对传统的检测系统来说需要更少的传感器设备，是一种更为经济简单的检测手段。

[1]廖瑞金,杨丽君,郑含博,等.电力变压器油纸绝缘热老化研究综述[J].电工技术学报,2012,27(5):1-12.

Liao Ruijin,Yang Lijun,Zhen Hanbo,et al.Reviews on oil-paper insulation thermal aging in power trans- formers[J].Transactions of China Electrotechnical Society,2012,27(5):1-12.

[2]赵笑笑,云玉新,陈伟根.变压器油中溶解气体的在线监测技术评述[J].电力系统保护与控制,2009,37(23):187-191.

Zhao Xiaoxiao,Yun Yuxin,Chen Weigen.Comment on on-line monitoring techniques for dissolved gas in transformer oil[J].Power System Protection and Control,2009,37(23):187-191.

[3]杨丽君,廖瑞金,孙会刚,等.变压器油纸绝缘热老化特性及特征量研究[J].电工技术学报,2009,24(8):27-33.

Yang Lijun,Liao Ruijin,Sun Huigang,et al.Inves- tigation on properties and characteristics of oil-paper insulation in transformer during thermal degradatoin process[J].Transactions of China Electrotechnical Society,2009,24(8):27-33.

[4]Morais R M,Mannheimer W A,Carballeira M,et al.Furfural analysis for assessing degradation of thermally upgraded papers in transformer insulation[J].IEEE Transactions on Dielectrics and Electrical Insulation,1999,6(2):159-163.

[5]郭亚丽,张云怀,孙大贵,等.变压器热老化过程中糠醛变化的高效液相色谱研究[J].分析科学学报,2007,23(4):410-412.

Guo Yali,Zhang Yunhuai,Sun Dagui,et al.Studies on furfural amount by HPLC in heat ageing process of transformers[J].Journal of Analytical Science,2007,23(4):410-412.

[6]Prosr P,Brandt M,Mentlík V,et al.Condition assessment of oil transformer insulating system[C].International Conference on Renewable Energies and Power Quality:Granada,Spain,2010:23-25.

[7]张镱议,廖瑞金,杨丽君,等.基于云理论的电力变压器绝缘状态评估方法[J].电工技术学报,2012,27(5):13-20.

Zhang Yiyi,Liao Ruijin,Yang Lijun,et al.An assessment method for insulation condition of power transformer based upon cloud model[J].Transactions of China Electrotechnical Society,2012,27(5):13-20.

[8]蔡红梅,陈剑勇,苏浩益.基于灰云模型的电力变压器故障诊断[J].电力系统保护与控制,2012,40(12):151-155.

Cai Hongmei,Chen Jianyong,Su Haoyi.Fault diagnosis of power transformer based on grey cloud model[J].Power System Protection and Control,2012,40(12):151-155.

[9]杨良军,熊小伏,张媛.基于灰色关联度和理想解法的电力设备状态维修策略[J].电力系统保护与控制,2009,37(18):74-78.

Yang Liangjun,Xiong Xiaofu,Zhang Yuan.Research on condition-based maintenance policy of electric power equipment based on grey correlation degree and TOPSIS[J].Power System Protection and Control,2009,37(18):74-78.

[10]李晓庆,陈尔奎,纪志成.基于MATLAB 单相变压器的仿真建模及特性分析[J].变压器,2005,42(3):48-54.

Li Xiaoqin,Chen Erkui,Ji Zhicheng.Simulation modelling and characteristic analysis of single-phase transformer based on MATLAB[J].Transformer,2005,42(3):48-54.

[11]Koochaki A,Kouhsari S M,Ghanavati G.Transformer internal faults simulation[J].Advances in Electrical and Computer Engineering,2008,8(2):23-28.

[12]Varga D,Loncar-Turukalo T,Bajic D,et al.Symbolic dynamic analysis of heart rate and blood pressuretime series of rats[C].International Symposium on IEEE Intelligent Systems and Informatics,2007:193-196.

[13]Kaddoum G,Gagnon F.Performance analysis of communication system based on chaotic symbolic dynamics[C].International Conference on IEEE Signals and Electronic Systems(ICSES),2010:307-310.

[14]Dale R,Spivey M J.From apples and oranges to symbolic dynamics:a framework for conciliating notions of cognitive representation[J].Journal of Experimental & Theoretical Artificial Intelligence,2005,17(4):317-342.

[15]Rajagopalan V,Ray A.Symbolic time series analysis via wavelet-based partitioning[J].Signal Processing,2006,86(11):3309-3320.

[16]Ray A.Symbolic dynamic analysis of complex systems for anomaly detection[J].Signal Processing,2004,84(7):1115-1130.

[17]Tewari D,Heydt G T.Load modeling utilizing symbolic dynamnics[J].IEEE Transactions on Power Engineering Review,2002,22(8):53-54.

[18]Fasano G,Franceschini A.A multidimensional version of the kolmogorov-smirnov test[J].Monthly Notices of the Royal Astronomical Society,1987,225:155-170.