开关磁阻起动/发电系统起动性能研究

昝小舒 陈 昊

（1.中国矿业大学电力工程学院 徐州 221116 2.中国矿业大学信电学院 徐州 221116）

0 引言

近年来，集成起动/发电系统得到了国内外研究者的广泛关注。开关磁阻电机（Switched Reluctance Motor，SRM）由于在结构、可靠性、容错性、可维护性、耐高温、转速范围、发电效率和起动转矩等方面具有综合优势，十分适合作起动/发电系统的核心电机[1-3]。国外在20 世纪末就开始了对开关磁阻起动/发电（Switched Reluctance Starter/Generator，SRS/G）系统的研究，并且成功地应用到了飞机的起动/发电系统[4,5]。国内，南京航空航天大学、西北工业大学等单位也与21世纪初开始了对SRS/G系统的研究，并进行了样机的设计[6,7]。

起动性能是衡量起动/发电系统优越与否的一个重要标志。对于起动过程要满足：①起动时间短并要求起动/发电系统能够在电源提供的能量下尽可能快地带动发动机起动；②起动容量小，通常起动容量越小，系统的电源体积和重量越小，成本越低；③起动电流小，目前起动/发电系统都是由大功率晶闸管、IGBT 和MOSFET 等功率器件进行控制，较大的起动电流必然对功率管的能力要求更高，系统的成本将增加；④起动频繁，对于应用到汽车、摩托等交通工具之上的起动/发电系统，需要频繁地起停发动机，这就要求起动/发电系统拥有很好的频繁起动能力。国内自从SRM 开始研究以来，已经有对SRM 起动性能有了一定的研究基础。文献[8]以仿真方式分析了电流斩波控制和角度控制对开关磁阻电机起动性能的影响，但对PWM 起动方式并没有涉及；文献[9,10]对12/10 结构的开关磁阻电机不同开通角下的一相转矩、合成转矩以及转速仿真分析，主要是对新型SRM 的性能进行对照分析；文献[11]对基本的起动过程进行了分析，但不够深入；文献[12]对起动方式、起动转矩和起动电流等参数进行了理论分析。因此，根据以上文献，对SRS/G 系统的起动性能研究不够深入和全面，只较多地涉及SRM 最基本的起动方式方法和仿真研究。

1 开关磁阻起动/发电系统组成

SRS/G 系统主要由主发动机、SRM、功率变换器、微处理器、电流检测、电压检测、位置检测、电池和负载等组成，如图1所示。SRM 首先由蓄电池供电电动运行，带动发动机转动到怠速以上，发动机点火起动；然后发动机带动SRM，SRM 转入发电运行，为负载电器供电和电池充电；在电池允许的情况下，SRM 可以电动运行，为发动机助力；在系统制动或减速时，SRM 可以实现发电制动，回收能量。

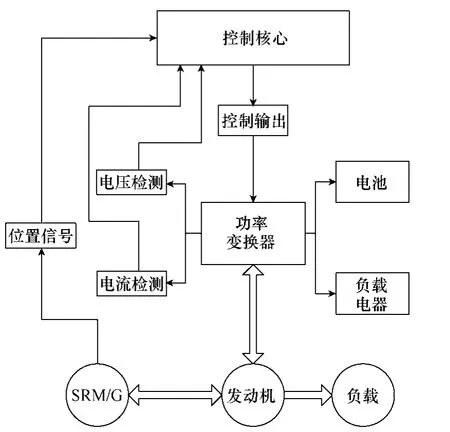
图1 SRS/G 系统Fig.1 System of SRS/G

2 起动特性分析

2.1 发动机起动转矩特性

目前飞机、汽车、坦克、摩托车等上面的发动机主要是汽油发动机和柴油发动机。以柴油发动机为例，根据柴油机的正常起动转矩转矩可以表示为

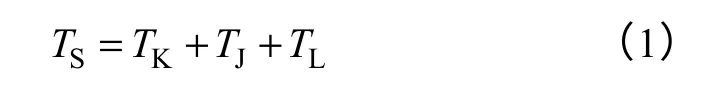
式中，TK为气体压缩负功产生的阻力矩；TJ为飞轮转动惯量矩；TL为摩擦阻力矩。

起动开始时，由于发动机静止，存在较大的静摩擦，因此起动阻转矩较大；随着转速的升高，静摩擦变成了滑动摩擦，阻转矩变小；在发动机点火前，由于压缩空气的阻力矩越来越大，阻力矩也变大。因此，柴油机的起动阶段的阻力矩是一个先大后小再大的过程，呈现下突的双曲线形状。图2所示为某发动机起动转矩曲线。

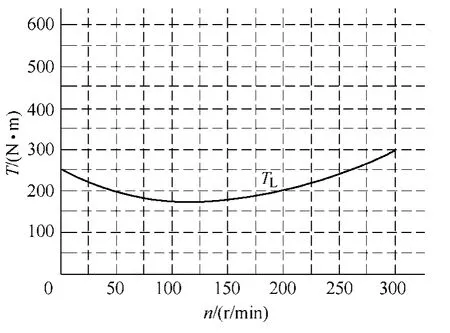
图2 发动机起动转矩曲线Fig.2 Start torque curve of engine

2.2 起动容量计算

为了使得发动机顺利点火，起动电机必须带动发动机运行到一定转速，最好是怠速ns以上。假设起动转矩最大为Tp，对于转速为np，则起动发动机阻功率为Pp=Tpnpπ/30。起动机的起动转矩应该最小值大于Tp，一般取1.2Tp。起动电机的最小起动功率可以估算为

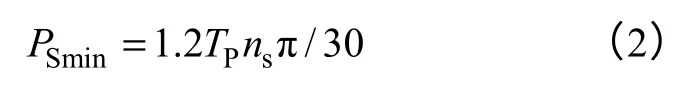
而起动电机的起动容量可以估算为

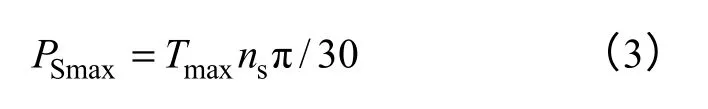
式中，maxT为起动电机的最大起动转矩。

2.3 起动时间计算

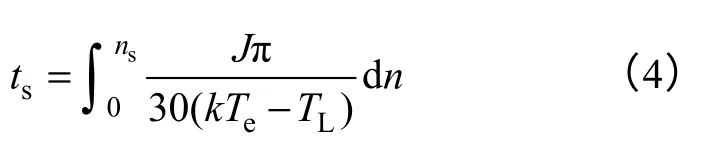
2.4 起动方法分析

发动机基本的起动方式主要有三种：恒转矩起动、恒转矩+恒功率起动和恒加速度起动。恒转矩起动方法如图3所示，在整个电机的起动过程中起动电机始终维持恒定的转矩直到起动结束。根据式（3）和式（4）可知，恒转矩起动时，起动转矩越大，起动时间越短，但是相应的需要更大的起动功率。恒转矩+恒功率起动方法如图4所示，在起动功率最大值一定的情况下，首先以恒转矩方式起动一直到最大起动功率，然后以恒功率的方式继续起动。该方法适用于起动功率受限制的场合，起动时间比恒转矩起动方式长。恒加速度方式如图5所示，该方法在发动机起动过程中一直维持起动加速度的恒定，起动转矩随着发动机阻转矩变化而变化，该种起动方法起动平稳，但必须在起动容量和起动要求的时间之间寻找合适的起动加速度。

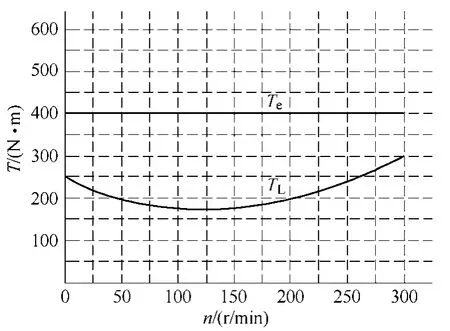
图3 恒转矩起动方法Fig.3 Starting method of constant torque

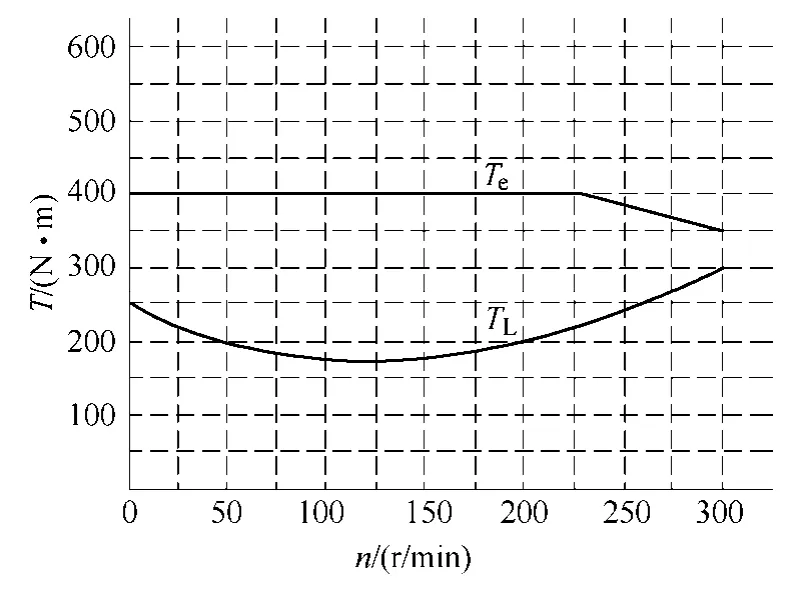
图4 恒转矩+恒功率起动方法Fig.4 Starting method of constant torque and constant power

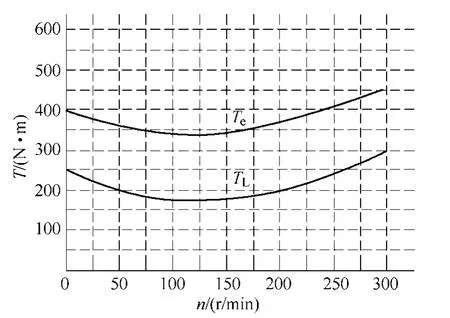
图5 恒加速度起动方法Fig.5 Starting method of constant acceleration

对于汽车发动机，一般情况下需要起动时间越短越好，这就需要起动机在其功率范围内以最大的转矩带动发动机起动，即以起动转矩最大进行起动；而在高档汽车中，一般对舒适度要求较高，在起动时间满足要求的情况下，一般还需要对起动转矩脉动进行控制，使得汽车发动机能够较平稳地起动。因此，本文根据发动机起动的要求，分别对起动转矩最大和起动转矩脉动最小两种情况进行SRS/G 系统的起动角度优化和起动控制策略设计。

3 SRS/G 系统PWM 控制下角度优化

根据控制参数的不同，开关磁阻电机主要三种控制方法：电流斩波控制、电压PWM 控制和角度位置控制。通常，开关磁阻电动机的基本控制方式是低速进行电流斩波或者电压斩波控制，高速角度位置控制。但在具体的应用中，如果机械地根据转速的大小来切换这几种控制方法，容易出现不少问题。如固定角度的电流斩波控制，在转速上升过程中容易出现负转矩，导致起动过程变长或者卡在某一转速中无法升速。所以必须将这几种控制方法灵活地组合起来才能获得较好的性能。电流斩波控制需要实时、快速、精确地检测绕组电流，角度位置控制需要快速、精确地计算角度位置，这两种控制方法对于控制器的要求比较高。电压PWM 控制实现简单、适用转速范围宽，对于起动/发电这样一个转速范围大的场合比较适用。但是单纯使电压PWM控制无法在整个速度段获得较好的控制效果，必须对不同转速下的开通角和关断角进行优化。因此，本文根据不同的场合，对转矩最大和转矩脉动最小两种情况进行了不同转速下的开通角和关断角的仿真优化。

3.1 仿真模型

为了方便优化研究，以一台功率500W12/8 结构SRM 为核心，建立了SRS/G 的Simulink 仿真模型。仿真模块如图6所示，由电机子模块、功率变换器子模块、机电转换子模块、电压PWM 控制子模块等组成。

优化仿真满足条件：母线电压维持24V；转速从100～600r/min 按照100r/min 递增；开通角从−10°到10°，按照1°递增；关断角从10°到30°，按照1°递增。

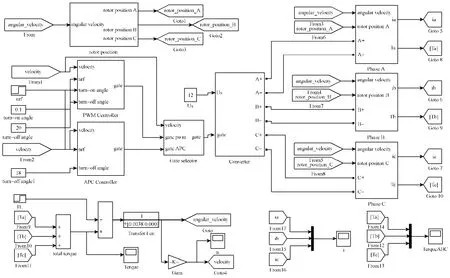
图6 SRS/G 仿真模型Fig.6 Simulation model of SRS/G system

3.2 起动角度仿真

起动时，如果始终以转矩最大的状态起动，起动时间必然是最短的。开关磁阻起动/发电系统中，不同的开通角和关断角，输出转矩是不一样的，为了使得起动转矩始终能够最大化输出，必须对开通角和关断角进行优化。根据磁共能关系，SRM 每相转矩可以表示为

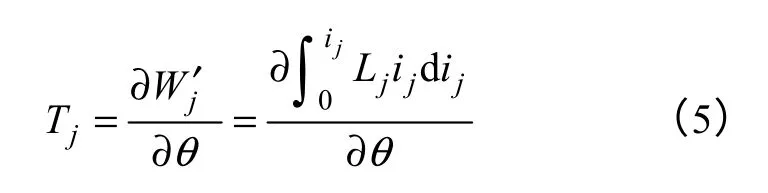
总转矩

通常以平均转矩来衡量起动转矩的大小，即

根据以上公式，对不同转速下，不同开通角和关断角下的平均转矩进行了仿真实验，图7分别是在100r/min、300r/min、500r/min 和700r/min时的仿真结果。

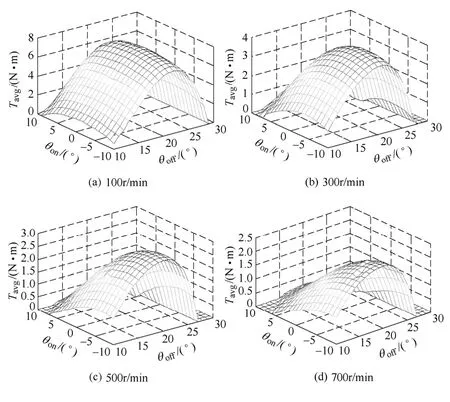
图7 基于转矩最大的开通角和关断角仿真结果Fig.7 Simulation results of turn-on angle and turn-off angle based on biggest start torque

由仿真结果可以看出，平均转矩受开通角影响较大，随着转速的升高，最优开通角逐渐变小；最优关断角也随着转速的升高而提前，但变化程度不大；随着转速的升高，开通和关断角都需要提前，可以使得电流能够有足够时间上升，从而使转矩能够以最大输出。通过仿真实验，各个转速下最优开通角和关断角数据见表1。

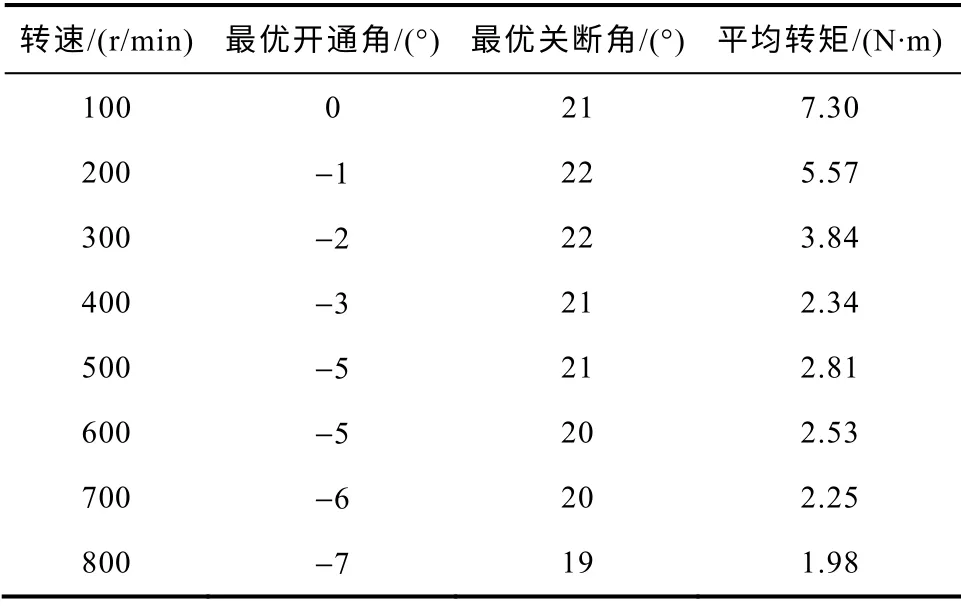
表1 基于转矩最大的开通角和关断角优化结果Tab.1 The optimization results of turn-on angle and turn-off angle based on biggest start torque

3.3 基于转矩脉动最小的电压PWM 控制方式下的开通关断角优化

根据电机电磁关系可知，SRS/G 的转矩和电流有着直接的关系，电流波形的形状直接影响到转矩的输出波形。通过控制电流波形和大小可以直接控制输出转矩的性能。不同的开通角和关断角下，绕组电流有较大的变化，从而导致转矩的变化。因此，存在优化的开通角和关断角可以使得电流满足一定的条件而输出转矩脉动较小。为计算方便取转矩脉动系数

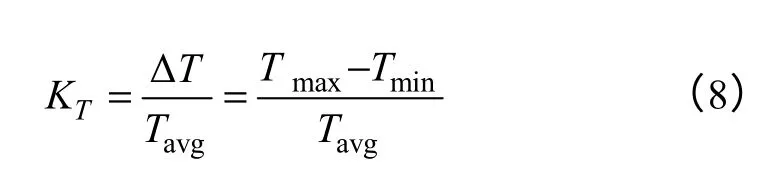
式中，Tmax和Tmin为这一时刻的转矩最大值和最小值；Tavg为平均电磁转矩。

根据以上公式，对不同转速下、不同开通角和关断角下的转矩脉动情况进行了仿真实验，图8分别是在100r/min、300r/min、500r/min 和700r/min时的仿真结果。

经过优化的各个转速下主开关器件的开通角和关断角转矩脉动最小优化结果见表2。根据表2 中的仿真结果可以看出：随着转速的升高，最优开通角逐渐提前，最优关断角逐渐推后。这是因为，随着转速的上升，电流上升时间变短，电流不能充分的上升就关断了，导致了合成电流峰谷之间间隙变大，同时电磁转矩的脉动也随着电流的变化而变大。通过提前开通角和延后关断角，可以使得电流建立时间变长，合成电流峰谷之间间隙变小，相应的电磁转矩脉动也相应变小。因此，通过控制开通角和关断角，可以改变合成电流的形状，进而改变转矩 的形状，转矩脉动的大小也随着改变。在不同的转速下，选择合理的开通角和关断角可以有效地减小电磁转矩脉动，尤其在需要起动比较平稳的情况下。但是，通过提前开通角和推后关断角，如果进入电感下降区域，将产生负转矩。减少转矩脉动是以牺牲电动效率为基础的。合理地选择适当的开通角和关断角是十分重要的。

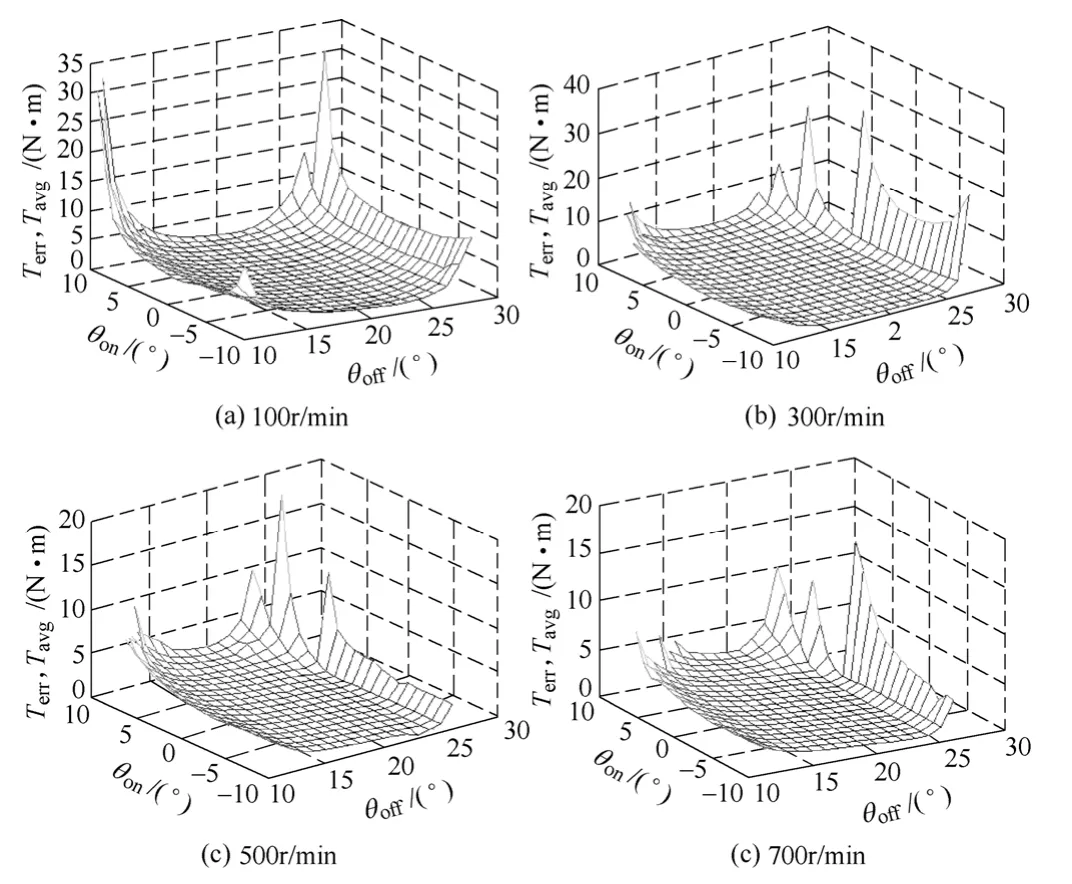
图8 基于转矩脉动最小的开通角和关断角仿真结果Fig.8 Simulation results of turn-on angle and turn-off angle based on minimal torque ripple

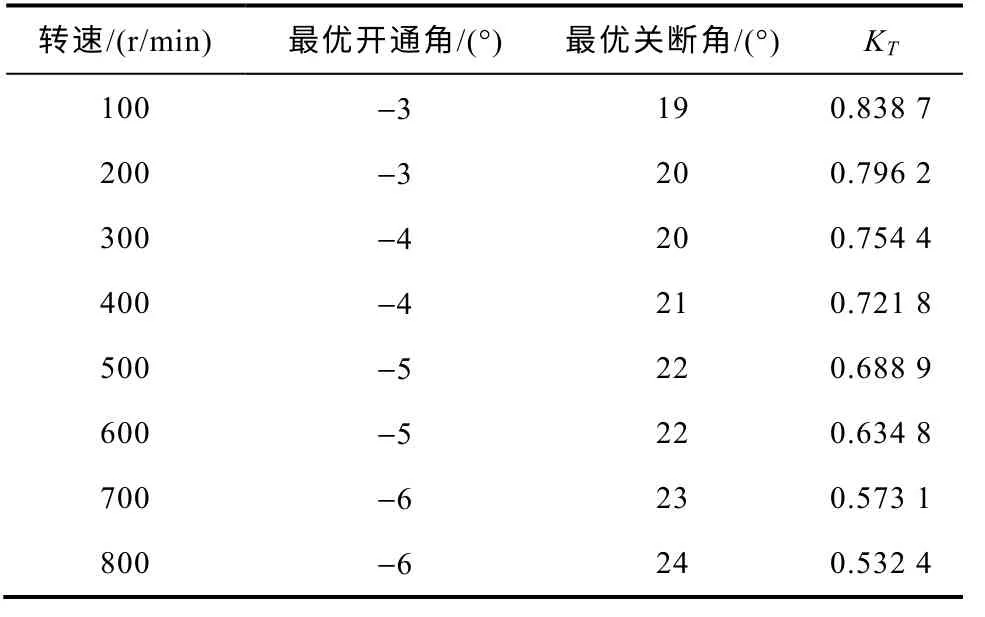
表2 基于转矩脉动最小的开通角和关断角优化结果Tab.2 The optimization results of turn-on angle and turn-off angle based on minimal torque ripple

4 SRS/G 系统起动控制策略

4.1 从静止到运行的起动控制

和大部分电机相比，SRM 具有起动转矩大和起动电流小的优点，在负载较轻的情况下可以直接起动。但是，如果负载过大，其起动电流瞬间也可能达到额定电流的数倍高，对功率变换器要求很高。因此，为了使得起动转矩足够大而且不超过限制，就必须合理地控制起动电流的大小。由于在SRM 起动控制中采用电压PWM 控制方法，因此控制起动电流的大小就是合理控制起动初始电压PWM 波的占空比。

为了获得不同初始电压PWM 占空比对起动性能的影响，本文对各种不同起动PWM 占空比进行仿真。取起动负载为1N·m，目标转速200r/min，起动占空比从5%一直到100%，每隔10%测试一次，具体的仿真实验情况见表3。

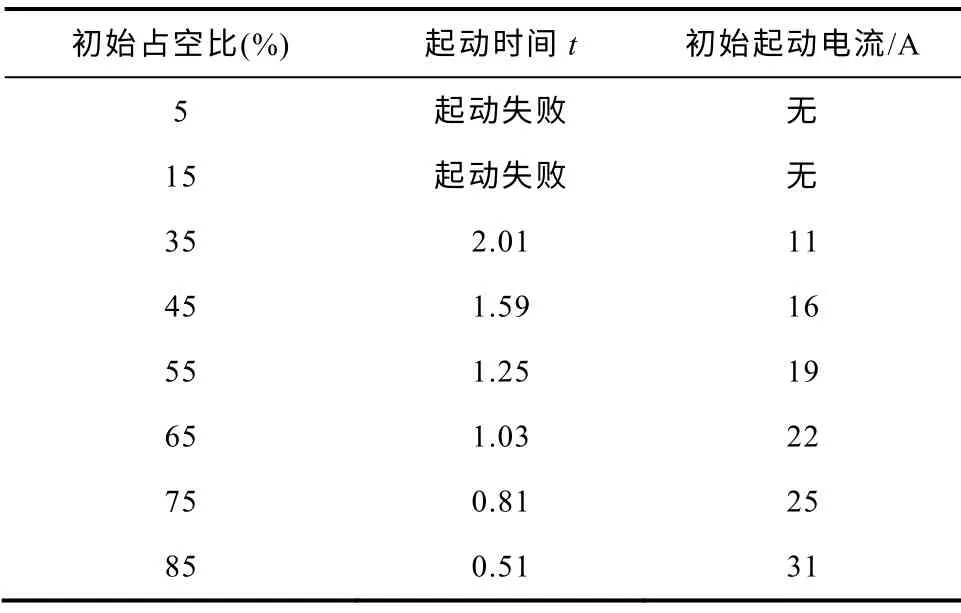
表3 不同初始电压PWM 占空比下的起动仿真结果Tab.3 Starting simulation results of different initial PWM voltage duty cycle

由仿真结果可以知道，从电机静止到运动，需要给出合适的PWM 占空比。在不同的起动负载情况下，起动占空比的要求也不一样，PWM 的占空比过大或者过小都不合适。因此，需要根据不同的情况，合理地调节起动初始PWM 的占空比大小，才能更好地起动电机。因此，设计出自调节起动PWM 占空比控制算法。

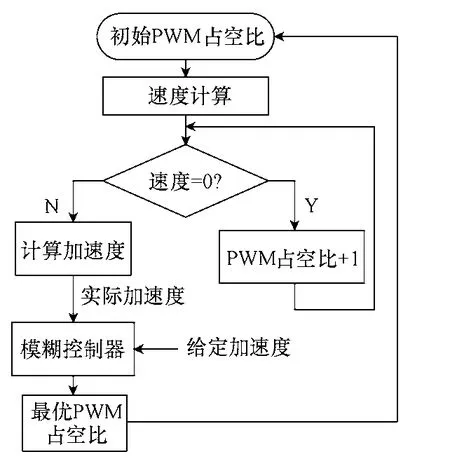
图9 初始PWM 占空比自估测过程Fig.9 Self assess flow of initial voltage PWM duty cycle

本文采用基于模糊控制的自适应初始PWM 占空比估测方法，如图9所示。初始PWM 占空比由上一次的模糊控制器计算给出，起动以后适当延时计算当前电机转速。如果转速为 0 说明电机起动PWM 占空比不够，起动失败，然后PWM 占空比自动加1，并延时重复计算电机转速；如果电机转速不为零，说明电机起动成功。电机起动成功后，计算起动阶段的加速度。如果加速度过大，说明初始PWM 占空比过大，下次起动需要减小；如果加速度过小，说明初始PWM 占空比过小，下次起动需要增加。加速度的加减通过模糊控制来实现，如图10所示。通过占空比的自我调节可以经过几次自学习之后，获得较好的起动PWM 占空比。

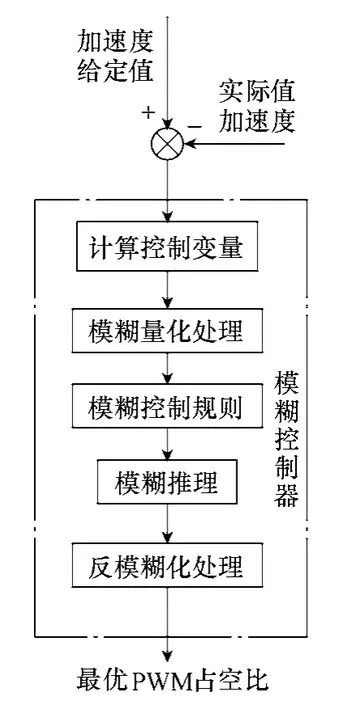
图10 起动加速度模糊处理Fig.10 The flowchart starting acceleration by fuzzy control

4.2 起动之后的控制策略

4.2.1 基于起动转矩最大的起动控制策略

基于转矩最大控制策略，需要在起动的时候使得转矩以最快的速度上升。本文采用滑模+PI 的控制策略，进行转矩最大的起动控制，如图11所示。滑模+PI 控制策略结合了滑模控制和PI 控制两种控制方法的优点，又摒除了两种的缺点。单独的滑模控制方法具有响应速度快，控制效果迅速的优点，但是在接近控制目标的时候，如发生转速振荡，不容易稳定；PI 控制方法在线性控制系统中具有良好的控制效果，但是对于SRS/G 这样一个严重非线性的控制系统，很难在整个速度范围内获得良好的控制效果，只能在小范围的控制中获得较好的稳定性。因此，在转矩最大控制中，主要以最大的速度起动发动机，在目标转速与实际转速的差较大的时候，采用滑模控制方法，使得转速尽可能快地上升；当目标转速与实际转速之差较小的时候，采用PI 控制，使得转速尽快地稳定在目标转速上，完成最大转矩起动控制。

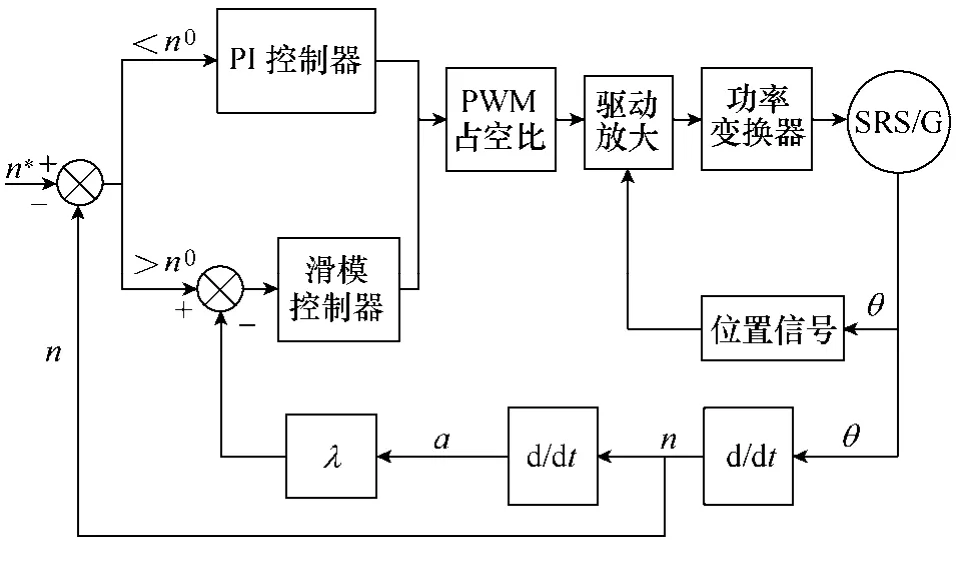
图11 基于滑模+PI 控制的转矩最大控制算法Fig.11 Maximal start torque algorithm by sliding mode+PI control

4.2.2 基于转矩脉动最小的起动控制策略

本文SRS/G 的起动过程采用了恒加速度起动方式。根据SRM 转子机械运动方程

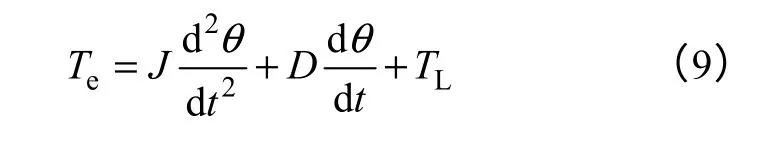
SRS/G 角速度ω和角加速度a的关系式

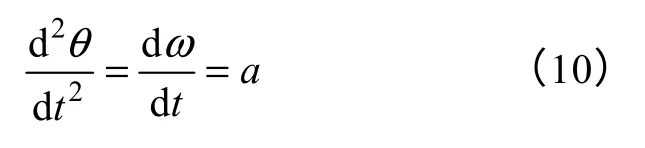
将式（10）代入式（9）可得

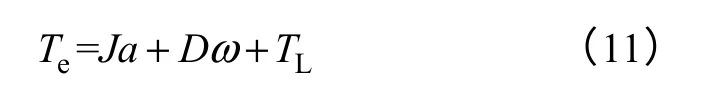
在电机起动过程中，转速不会太高，系统的粘性摩擦系数D很小，可以认为系统的粘性转矩Dω近似为0。式（11）可以近似为

由式（12）可知，通过控制加速度就可以控制电磁转矩，使之随着发动机的阻转矩变化而变化，使得转速平稳上升。SRS/G 由于结构和功率变换器严重的非线性，它的起动转矩脉动较大，而一般的控制方法无法直接控制转矩。本文采用加速度控制，间接地控制了起动转矩，可以对起动过程中较大的转矩脉动进行消减控制。

同样采用如图12所示的滑模+PI 的控制方法，在转矩脉动最小中，主要以平稳加速度起动发动机，在目标加速度与实际加速度相差较大的时候，采用滑模控制方法，使得加速度尽可能快地上升到目标加速度；当目标加速度与实际加速度相差较小的时候，采用PI 控制，使得加速度尽快地稳定在目标加速度上，实现恒加速度起动。

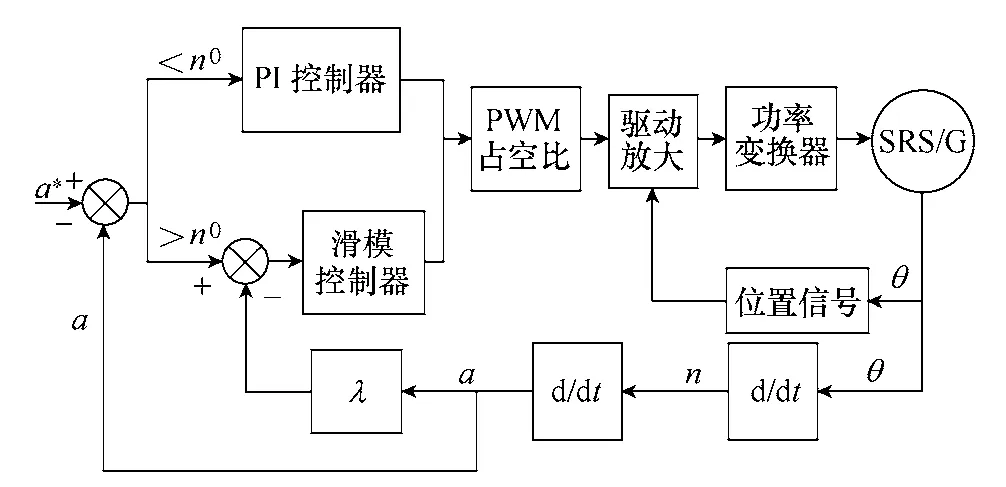
图12 基于滑模+PI 控制的转矩脉动最小控制算法Fig.12 Minimum start torque ripple algorithm of sliding mode+PI

5 实验平台及实验结果

5.1 实验平台

为了验证设计的SRS/G 系统的起动控制方法的有效性，采用SRS/G 系统样机实验平台进行起动性能测试。所以实验平台如图13所示，该平台主要包括一台三相12/8 结构的SRM、额定功率500W 发动机（由一台3kW 的SRM 模拟），功率变换器、负载、电池和微机控制系统等。

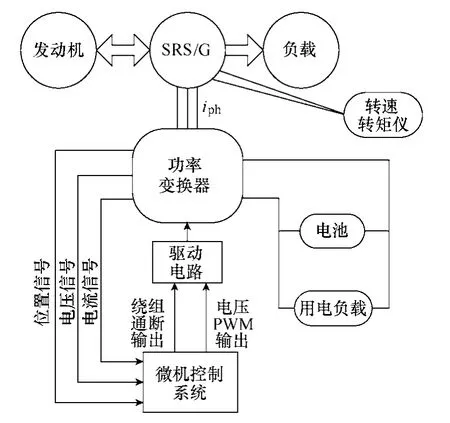
图13 SRS/G 系统实验平台示意图Fig.13 Experiment platform of SRS/G

5.2 从静止到运行的实验验证

图14～图16所示分别为起动转矩为0.5、1.0和1.5时，由静止到运行的起动电流波形和转速波形。采用初始PWM 占空比估测算法之后，可以看出，在三种不同的起动转矩之下，三者的起动时间相差不大，都在2s 左右，基本可以完成不同转矩的快速起动。在转矩0.5N·m 的时候，起动电流15A左右；在转矩1.0N·m 的时候，起动电流26A 左右；在转矩1.5N·m 的时候，起动电流40A 左右。通过电流可以看出，在不同的起动转矩下，起动电流的大小和起动转矩基本成正比，也就是初始电压PWM起动占空比和起动转矩基本成正比。通过采用初始PWM 占空比估测算法，可以在不同的起动转矩下实现不同初始PWM 占空比的估算。

图14 转矩为0.5 N·m时起动波形Fig.14 The starting waveforms basedon the torque of 0.5N·m

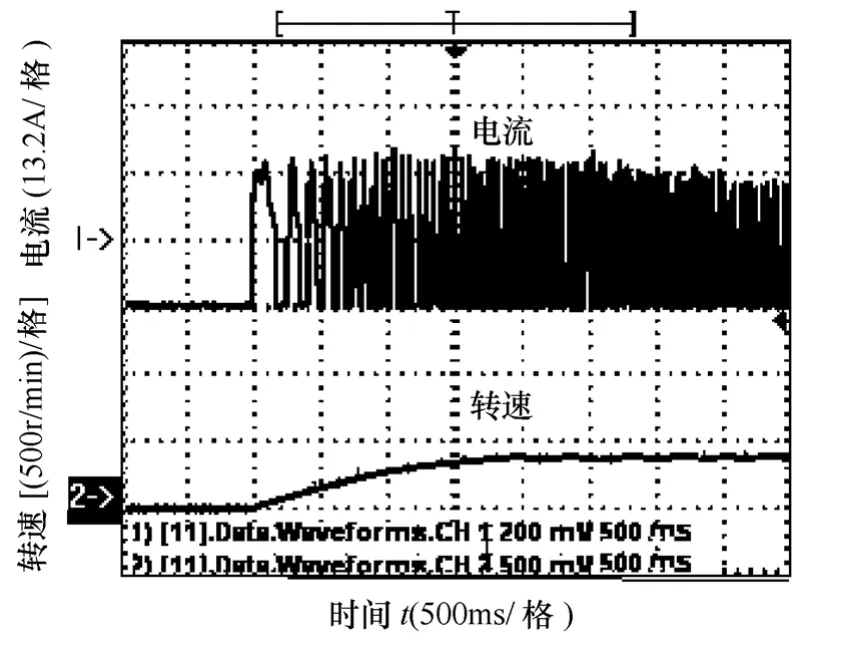
图15 转矩为1.0 N·m时起动波形Fig.15 The starting waveforms basedon the torque of 1.0N·m

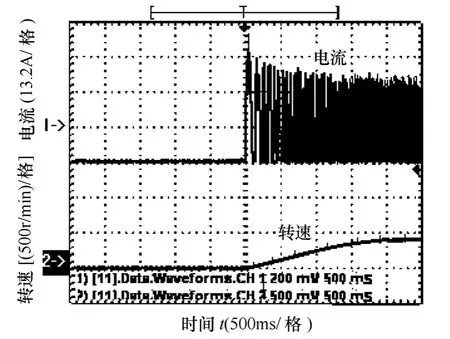
图16 转矩为1.5N·m时起动波形Fig.16 The starting waveforms based on the torque of 1.5N·m

5.3 起动之后的控制策略

起动之后，分别采用基于起动转矩最大和转矩脉动最小两种控制策略进行样机实验。两种控制策略下的起动电流和转速实验波形如图17所示，图17是起动转速为400r/min、600r/min 和800r/min时的采用起动转矩最大方法下的起动波形；图18是起动转速为400r/min、600r/min 和800r/min时的采用转矩脉动最小方法下的起动波形时。由实验结果可以看出：在400r/min、600r/min 和800r/min时，采用起动转矩最大方法时，起动时间分别是2s、3s 和4s；采用转矩脉动最小方法时，起动时间分别是4s、6s 和8s；采用转矩最大起动方式明显可以在较短的时间内完成发动机的起动。而采用转矩脉动最小方式起动时，可以看出起动转速基本成一条直线上升，而且电流波动较小，其起动脉动较小，可以完成较稳定的起动。

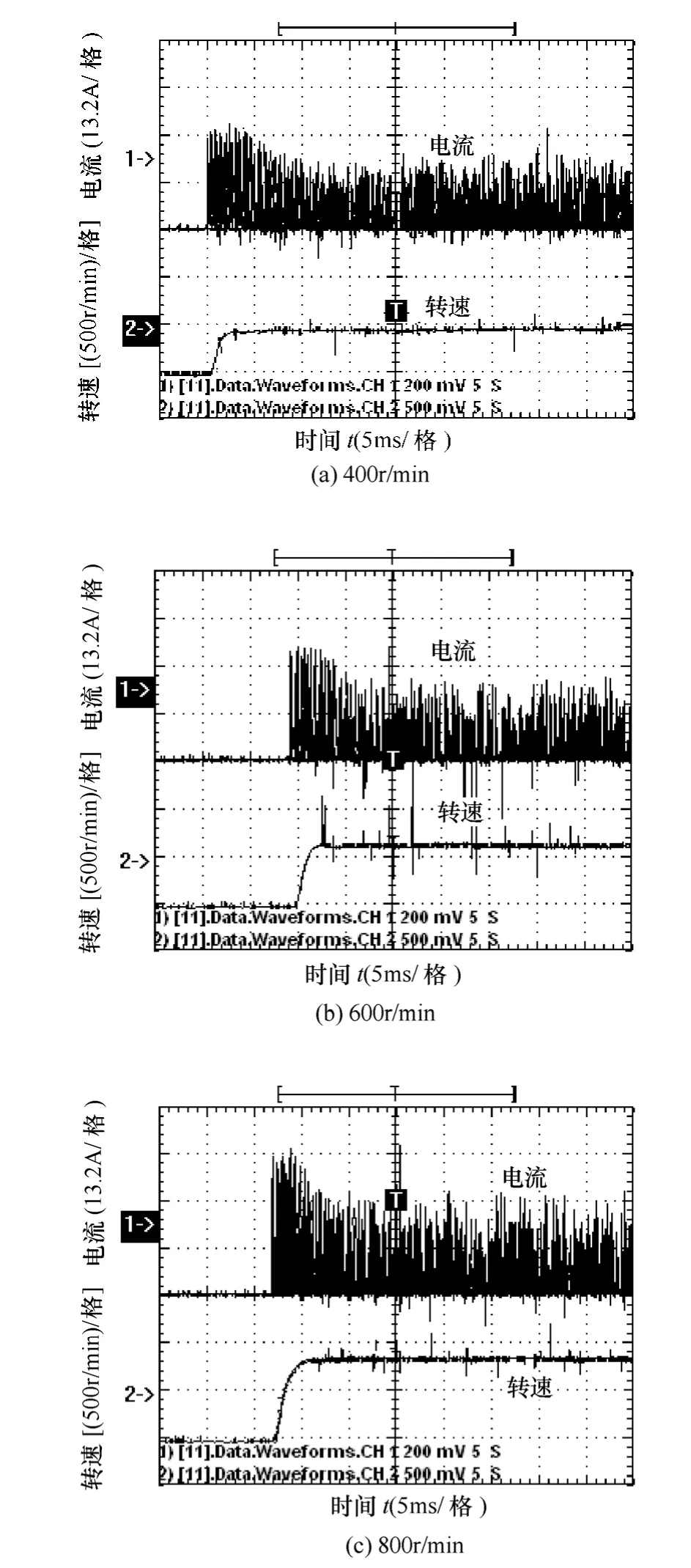
图17 不同转速下最大转矩起动实验波形Fig.17 The starting experiment waveforms of different speed based on maximal start torque

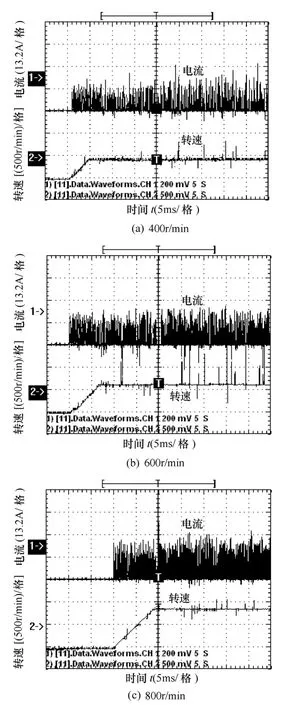
图18 不同转速下最小转矩脉动起动波形Fig.18 The starting experiment waveforms of different speed based on minimum start torque ripple

6 结论

本文对SRS/G 系统起动性能进行了研究。首先分析了SRS/G 系统的起动特性，得出基于转矩最大和转矩脉动最小两种起动要求。然后针对这两种要求，SRS/G 系统PWM 控制下角度进行了仿真优化，并得出了不同转速下的最优主开关的开通角和最优关断角。然后对 SRS/G 系统由静止到运行的起动PWM 占空比估测算法和起动后两种起动要求下的控制策略进行了设计。最后采用SRS/G 系统样机平台对设计的起动控制策略进行了实验验证。实验结果表明所设计的控制方法的有效和正确性。本文所进行的优化和起动控制策略的设计对SRS/G 系统的理论研究和实际应用都有着较好的参考意义。

[1]王宏华.开关型磁阻电动机调速控制技术[M].北京:机械工业出版社,2002.

[2]Richter E,Lyons J,Ferreira C,et al.Initial testing of a 250kW starter/generator for aircraft application[C].Proceedings of SAE Aerospace Atlantic Conference,1994:941160.

[3]昝小舒,陈昊.基于自抗扰控制的开关磁阻电机转速闭环性能[J].电工技术学报,2012,27(7):17-25.

Zan Xiaoshu,Chen Hao.Rotating speed closed loop study of switched reluctance motor based on auto disturbance rejection control[J].Transactions of China Electrotechnical Society,2012,27(7):17-25.

[4]Elbuluk M E,Kankan M D.Potential starter/ generator technologies for future aerospace applications[J].IEEE Aerospace and Electronic Systems Magazine,1997,12(5):24-31.

[5]Miller J M.Starter-alternator for hybrid electric vehicle:comparison of induction and variable reluctance machines and drives[C].IEEE Industry Applications Society Annual Meeting,1998,1:513-523.

[6]刘闯,朱学忠,曹志亮,等.6kW 开关磁阻起动/发电系统设计及实现[J].南京航空航天大学学报,2000,32(3):245-250.

Liu Chuang,Zhu Xuezhong,Cao Zhiliang,et al.Design and research of 6kW switched reluctance starter/ generator system[J].Journal of Nanjing University of Aeronautics & Astronautics,2000,32(3):245-250.

[7]李声晋,卢刚,马瑞卿,等.开关磁阻组合起动机/发电机设计及试验[J].中国电机工程学报,2000,20(10):10-14.

Li Shengjin,Lu Gang,Ma Ruiqing,et al.Design and test on switched reluctance integral starter/generator[J].Proceedings of the CSEE,2000,20(10):10-14.

[8]杨岳峰,张奕黄,王素杰.用于电动车辆的SRM 起动性能研究[J].北京交通大学学报,2007,31(5):114-116.

Yang Yuefeng,Zhang Yihuang,Wang Sujie.Study on starting performance of SRM by electric vehicle[J].Journal of Beijing Jiaotong University,2007,31(5):114-116.

[9]刘强,全力,苏宝平,等.汽车起动/发电系统用开关磁阻电机起动性能分析[J].微电机,2005,38(2):16-18.

Liu Qiang,Quan Li,Su Baoping,et al.Start-performance analysis of the switched reluctance motor using in ISAD system[J].Micromotors,2005,38(2):16-18.

[10]朱小襄,张磊,张今朝,等.开关磁阻电动机起动性能仿真[J].微电机,2008,41(9):85-89.

Zhu Xiaorang,Zhang Lei,Zhang Jinzhao,et al.Dynamic simulation of switched reluctance motor based on Matlab/Simulink[J].Micromotors,2008,41(9):85-89.

[11]景绍学,韦剑强.开关磁阻电机起动运行特性分析与控制策略研究[J].微电机,2010,43(5):31-34.

Jing Shaoxue,Wei Jianqiang.Analysis of starting operating characteristic and study on the corresponding control strategies for switched reluctance motor[J].Micromotors,2010,43(5):31-34.

[12]王素杰,杨岳峰.开关磁阻牵引电机的起动控制[J].电机与控制应用,2007,34(10):51-56.

Wang Sujie,Yang Yuefeng.Starting performance of switched reluctance motor for electric traction[J].Electric Machines & Control Application,2007,34(10):51-56.