基于变结构自抗扰的永磁电动机速度控制系统
2015-06-24黄守道冯垚径周腊吾李孟秋邓秋玲
黄 庆 黄守道 冯垚径 周腊吾 李孟秋 邓秋玲
(1.湖南大学电气与信息工程学院 长沙 410082 2.株洲南车时代电气股份有限公司 株洲 412001 3.湖南工程学院电气与信息工程学院 湘潭 411104)
0 引言
近年来,随着新颖的永磁同步电动机(Permanent Magnet Synchronous Motor,PMSM)非线性控制理论的发展,在矢量控制的基础上采用先进的复杂控制策略如自适应神经网络控制[1]、模糊PID 控制[2]、滑模变结构控制[3]和自抗扰控制[4]等构成内外环控制器,可实现调速系统的高性能控制,这些方法自身都各有优缺点。在这些非线性控制策略中,滑模变结构控制具有对系统参数变化适应性强、鲁棒性好等特点,在非线性系统分析与控制中的应用,具有十分可观的研究前景。由于开关的切换动作所造成的控制的不连续性,使得滑模变结构控制系统存在“抖振”问题[5],文献[6]采用了串级复合滑模控制,通过在速度环增加积分环节来消除滑模控制的力矩抖动,从而能够有效地减弱抖振。文献[7]采用了自适应滑模变结构控制,保证变结构控制器控制增益的合理性,对于系统的不匹配不确定性扰动具有自动调节的能力。文献[8]采用了一种新型的滑模趋近率控制策略,能够解决时间延迟的问题使得进一步削弱抖振。但是此类控制方法在伺服电动机低速甚至超低速控制中,在负载转矩突变及控制系统参数变化的情况下仍然存在抖振的问题,使得伺服系统的位置准确度无法提高,因此需要采用更好的复合控制策略解决永磁同步电动机的速度环控制问题。
自抗扰控制器是一种不依赖被控对象数学模型的新型控制技术,能自动检测并补偿被控对象的内外扰动,控制对象的参数发生变化或者遇到不确定性扰动时能结合非线性反馈组合实现很好的控制效果,具有较强的适应性、鲁棒性和可操作性,然而自抗扰控制器中可调参数较多且不便于实际操作和整定[9]。文献[10]提出了一种无需参数整定的自抗扰控制器,在这种结构下,无需参数整定,可以有效控制PMSM 的转速和转矩。但是此类控制方法在应用于交流伺服系统高速控制中,且受到转动惯量、负载转矩突变及摩擦力等系统扰动影响时,抗扰动能力稍差,且超调较大,其控制策略难以达到高稳态准确度要求。
因此,本文结合滑模变结构和自抗扰两种控制技术的优势,提出了一种PMSM 滑模自抗扰控制系统。将滑模控制引入到速度及电流自抗扰控制器(Active-Disturbance Rejection Controller,ADRC)的设计中,通过对控制器中非线性状态误差反馈的参数自整定改进,使控制器保持了原自抗扰控制器特点又使可调参数在切换时平滑过渡,减小了系统的误差,改善了系统控制性能,同时在保证系统动态性能的情况下,提高了系统鲁棒性和系统内部抗扰动的能力,并且在永磁同步电动机调速控制系统中保证系统的高低速控制性能,达到系统调速范围宽的目的。通过仿真及实验验证,改进后的系统与典型的自抗扰控制器(ADRC)相比,具有响应速度快、超调小、稳态准确度高和调速范围宽的优点,且对转动惯量、负载转矩突变及摩擦力等系统扰动影响具有很强的鲁棒性。
1 PMSM 的数学模型
三相永磁同步伺服电动机的数学模型是一个多变量、非线性和强耦合系统。本系统采用了三相正弦波电流驱动的表面贴装式永磁同步电动机(SPMSM)为被控对象,Ld=Lq=L。假设转子上没有阻尼绕组,转速在基速以下时,在定子电流给定的情况下,id=0 控制,可以更有效地产生转矩。基于永磁同步电动机的理想数学模型,SPMSM 的数学模型在dq 轴坐标系下可以描述为[11,12]
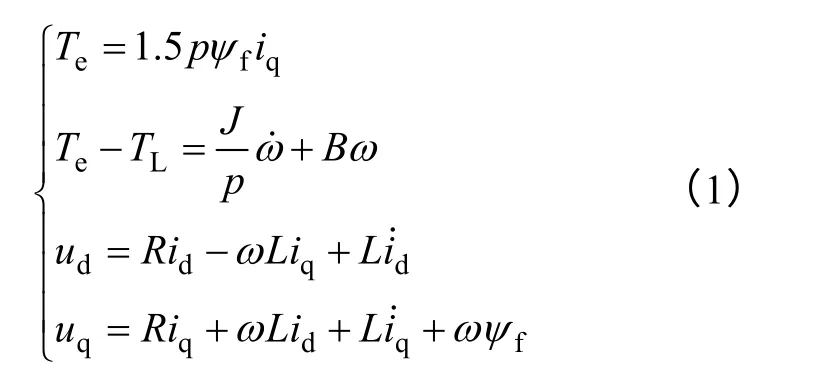
式中,id、iq为电动机定子电流d、q 轴分量;ud、uq为定子电压d、q 轴分量;R为定子绕组电阻;L为定子d、q 轴自感;ψf为转子永磁体产生的磁链;TL为负载转矩;Te为电磁转矩;J为转子转动惯量;B为阻力系数;p为极对数;ω为转子角速度;θ为转子的位置角。
2 滑模变结构自抗扰控制器的数学模型
2.1 自抗扰控制的数学模型
自抗扰控制器主要由跟踪微分器(Tracking Differentiator,TD)、扩张状态观测器(Extended State Observer,ESO)和非线性状态误差反馈控制律(Nonlinear States Error Feed-Back,NLSEF)三部分组合而成。本文采用转速电流双闭环控制,使其成为一个整合的自抗扰速度环,因此采用了二阶自抗扰控制器。
在这里,自动估计补偿扰动能力是自抗扰控制器的关键所在,适当选取跟踪微分器、扩张状态观测器和非线性状态误差反馈控制律中的非线性函数及参数,二阶被控对象的状态方程[13]可描述为
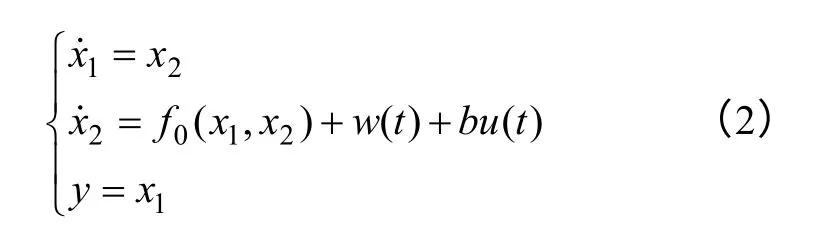
式中,u(t)为系统的控制量;y为系统的被控对象输出;x1、x2构成系统运动全部信息的状态变量;b为系统控制量增益;f0(x1,x2)是系统“内部扰动”,为已知量;w(t)是系统“外部扰动”,为未知量,则内部扰动与外部扰动的总和为系统的“总扰动”。
对于PMSM 的典型二阶自抗扰控制器设计如下:
(1)首先,对于电动机的给定转速输入信号v设定线性跟踪微分器(TD)方程为
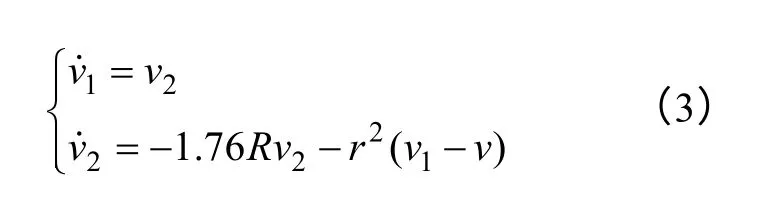
式中,v为输入信号;v1为v安排适当的过渡过程是跟踪输入信号;v2为跟踪输入信号v1的微分;可调参数r为速度因子,r越大,跟踪速度越快。
(2)通过对电动机实际输出y,设计非线性扩张状态观测器,把含有未知扰动的非线性不确定对象转化成“积分串联型”对象,u(t)可为电动机的 d轴或 q 轴上的电压,扩张状态观测器(ESO)方 程[14-16]为
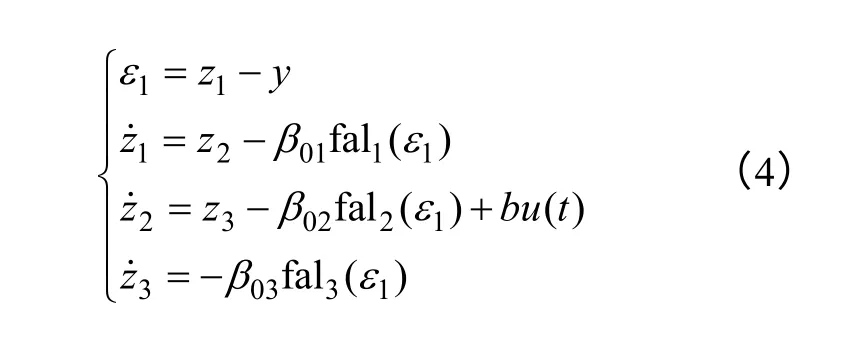
式中,z1为系统输出y的跟踪信号;z2为z1的微分信号;z3为未知扰动的估计值;ε1为误差信号;β01、β02和β03为输出误差校正增益(三个可调参数);fal(·) 为最优综合控制函数,其表达式为
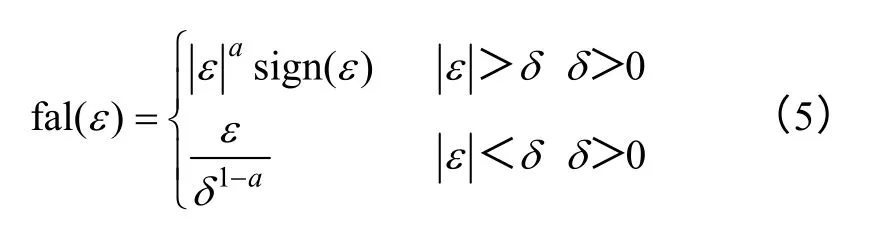
式中,a为非线性因子,0<a<1;δ为滤波因子;ε为输入误差变量。
(3)非线性状态误差反馈控制律(NLSEF)是由TD 产生的各阶导数和ESO 产生的状态变量估计之间的误差“非线性组合”,其与ESO 对总扰动的补偿一起组成控制量,NLSEF 主要作用是设计控制量u0(t),使其控制好二阶积分串联型被控对象,非线性状态误差反馈控制律的方程为
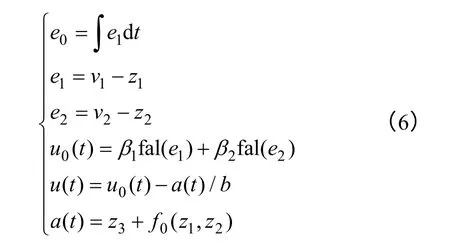
式中,e1、e2分别为误差和误差微分信号;β1、β2分别为误差和误差微分增益;u(t)为补偿控制量;u0(t)为设定控制量;f0(z1,z2)是系统已知部分,为内部扰动,如果ESO 能对a(t)进行有效的估计,例如电动机的负载扰动属于a(t),便可以抑制负载扰动的影响,自抗扰的意义在于补偿项-a(t)/b,用来一起估计和补偿系统的未建模动态和未知外部扰动。
ADRC 利用ESO 估计受控对象状态变量和总扰动实时作用量,并给予补偿,从而设计出合理的非线性状态误差反馈控制律,适当选取参数,提高了系统控制准确度,使控制器具有较强的适应性和鲁棒性,典型二阶ADRC 控制器结构如图1所示。
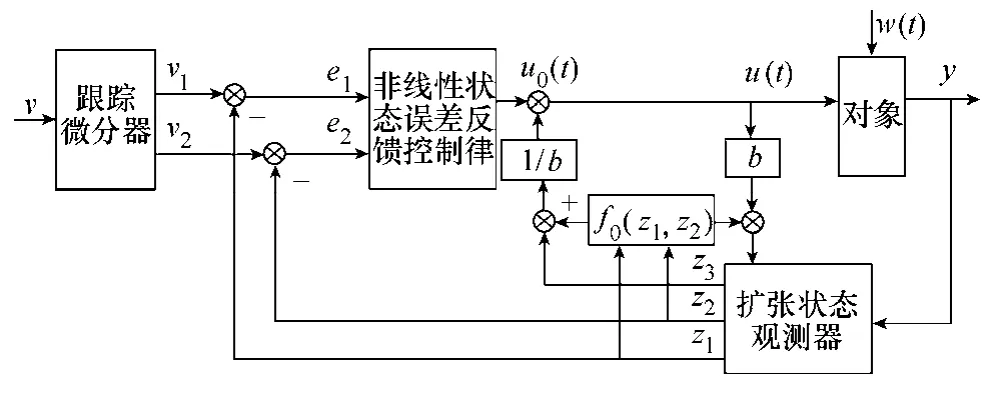
图1 典型二阶自抗扰控制器结构图Fig.1 The block diagram of typical second-order ADRC controller
2.2 滑模扩张状态观测器的数学模型
滑模控制(Sliding Mode Control,SMC)是变结构控制(Variable Structure Control,VSC)系统的一种控制策略。它本质上也是一类特殊的非线性控制,根据系统状态的变化,迫使系统按照预定滑动模态渐近稳定。由于滑动模态可不依赖于对象参数及扰动进行设计,使得滑模变结构控制系统具有快速响应、稳态准确度高和转矩平滑等特点,同时抑制参数和负载变化所引起的扰动。
针对电动机变频调速单输入单输出控制系统,设计滑模变结构控制系统步骤如下:
(1)设计滑膜切换向量函数s(x),取s(x)=cx=,滑动模态运动的渐近稳定性取决于切换向量函数,其中,xi=x(i-1)(i=1,2,… ,n)为系统状态及其各阶导数,选取适当的常数c1,c2,… ,cn-1,使得构成稳定的滑模面。
(2)设计滑动模态最佳趋近控制率u(x),使得滑动模态运动是系统沿着切换面s(x)=0 上运动,系统进入滑模面状态,但在实际中,系统运动点沿切换面上下穿动,存在抖振的问题。
通过将自抗扰技术与滑模变结构控制器相结合,对式(4)作适当变形,得出等价式为
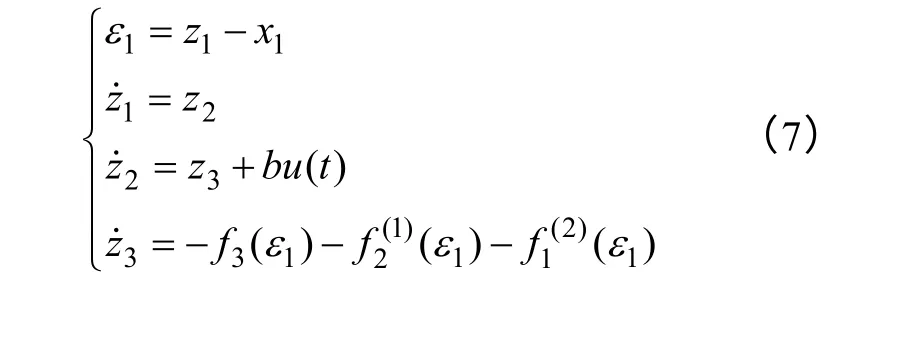
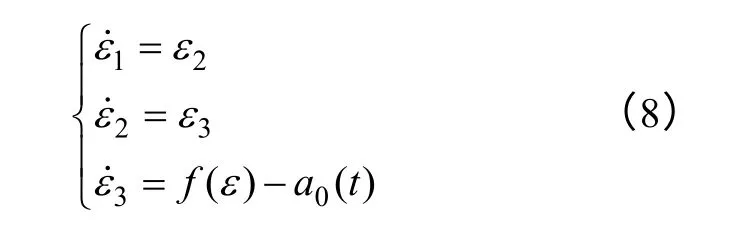
只要选取合适的最优控制函数f(ε)就能保证滑模扩张状态观测器稳定,这也保证了系统的稳定性。对于电动机控制系统,设计滑模切换向量函数为
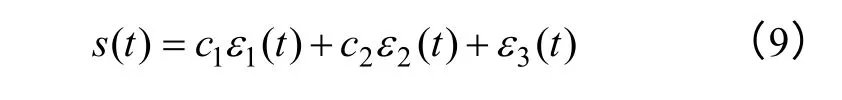
适当选取常数c1、c2,使得多项式p3+c2p2+c1p+1(p为Laplace 算子)为Hurwitz 稳定,且具有较大的稳定裕度。令函数f(ε)为
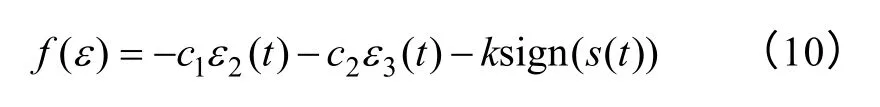
使得滑模扩张状态观测器稳定。式(10)中k为可调参数,sign(·) 为开关符号函数
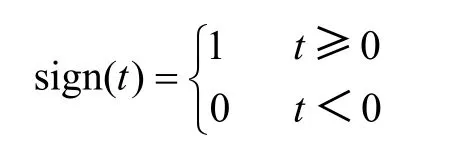
对于系统稳定证明如下。
对切换向量函数s(t)微分,同时将式(9)代入函数式中,可得
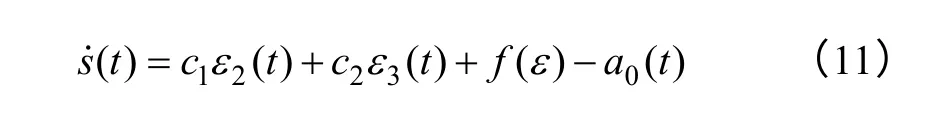
将式(10)代入式(11)得
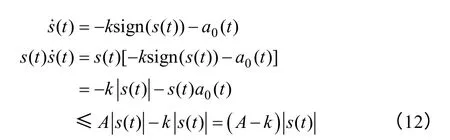
式中,选取合适k值,使得k>A,则,根据滑模控制的Lyapunov 稳定性要求,系统进入滑模面,从而保证了系统的稳定性。为了削弱抖振,用继电特性函数θ(s)来使控制量连续化,即用θ(s)函数替代式(10)中不连续的常规滑模控制器开关符号函 数sign(·)。继电特性函数表达式为,式中,δ1为较小的正的常数,是可调参数。
2.3 滑模非线性状态误差反馈控制器的数学模型
从式(3)中可知,对于输入给定信号v(t),v1(t)跟踪输入信号v(t),而v2(t)是v1(t)的微分且是一种“品质”很好的微分;从式(3)和式(4)可知,z1(t)和z2(t)可很好地跟踪原系统x1(t)和x2(t)状态变量,是对系统状态变量的重构,因此两组变量之间的误差e1=v1-z1,e2=v2-z2为对象参考输入v(t)的状态误差;由于,对式(3)和式(7)进行推导,则有
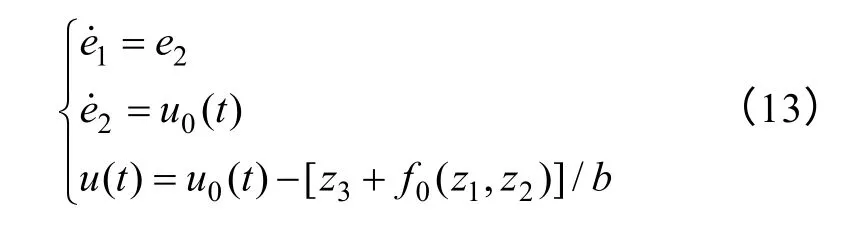
用误差的“非线性配置”来实现“非线性状态误差反馈”控制,用滑模控制函数设计控制量为
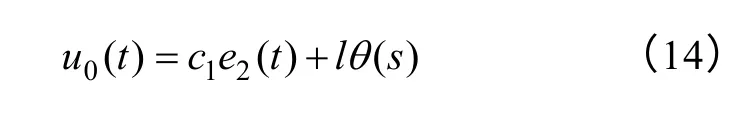
从而保证系统稳定。式中,l为可调参数;θ(s)为继电特性函数,以削弱系统抖振,其表达式为θ(s)=,δ2为较小的正可调参数,常数c1和滑模面的选取以及稳定性分析如2.2 节所述,由于此处定义误差为输入信号与输出信号之差,故控制量u0(t)为“正”。
由以上分析可知,改进后的滑模变结构自抗扰器中变结构扩张状态观测器(ESO)和滑模非线性状态误差反馈控制律(NLSEF)各含有两个可调参数,且可调参数个数不受被控系统阶次的影响。与改进前典型自抗扰控制器相比,可调参数有所减少,这使得参数整定变得更简单。
3 PMSM 变结构自抗扰速度控制系统
3.1 基于变结构自抗扰控制的速度电流环调节器
在同步旋转坐标系下,由式(1)推导得永磁同步电动机速度电流环的二阶动态方程为
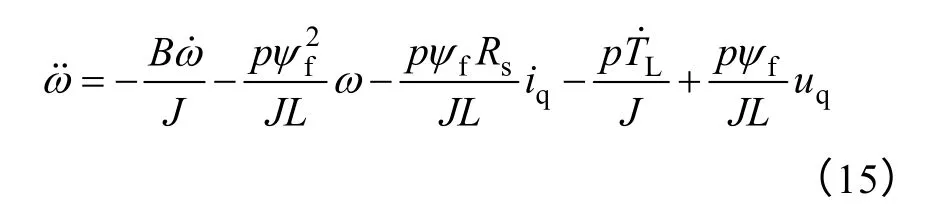
令
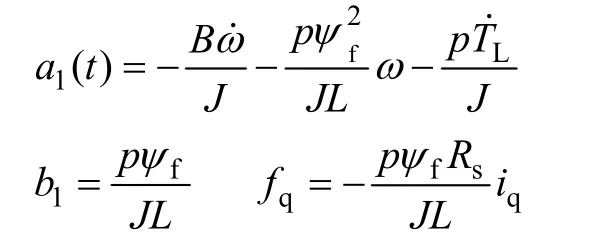
则式(15)可简化为
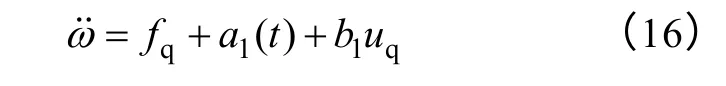
式中,fq为系统已知扰动;a1(t)为系统未知负载扰动;通过这两项可以有效地估计系统速度电流环的总扰动,并对总扰动进行补偿,对负载扰动有很好的鲁棒性;在有位置传感器的条件下,dω/dt为已知量,其微分亦为已知量,可得速度电流环的状态方程为
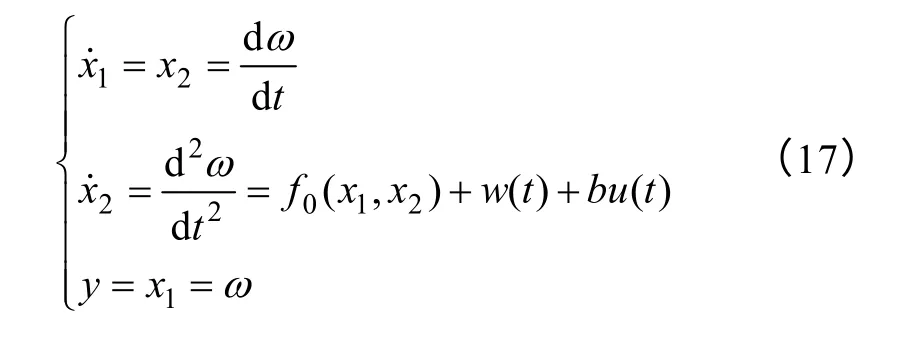
由此可知,其状态方程与自抗扰控制器式(3)相同。故可依据式(4)、式(8)、式(11)、式(14)和式(15)来设计速度电流环滑模自抗扰控制器,其结构如图2所示。图中,ω*是给定转子速度;是q 轴给定电压;ω为转子速度反馈信号;v1是ω*的跟踪信号;v2为ω*的微分信号;z1为ω的跟踪信号;z2为z1的微分信号;z3为系统不确定部分观测量,即未知扰动量a1(t);fq为已知扰动观测量。此处微分的作用不同于PID 控制中的微分,它对“噪声”不是起放大作用,而是起抑制作用。
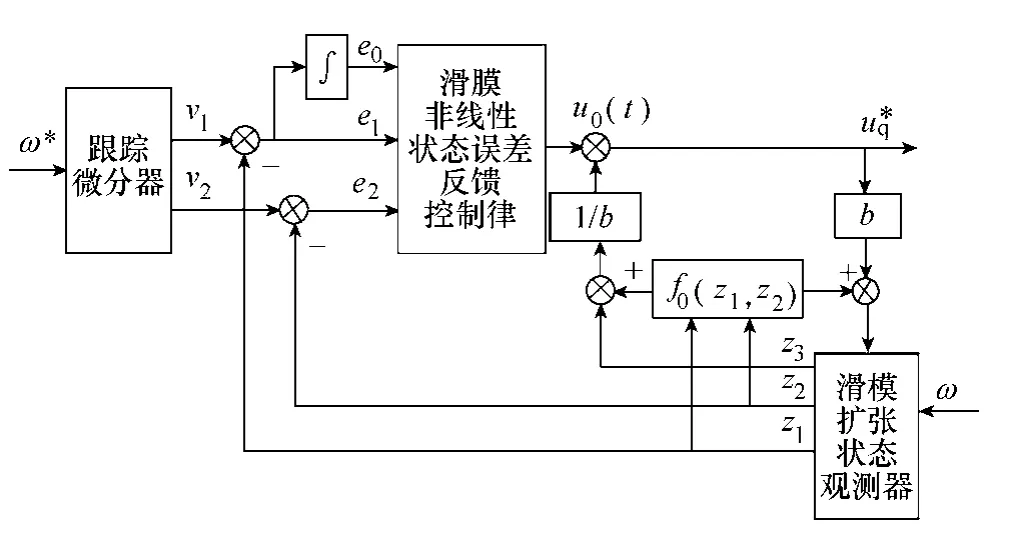
图2 速度电流环滑模自抗扰控制器的总体框图Fig.2 Speed current loop overall block diagram of VS-ADRC controller
在滑模自抗扰控制器中,跟踪微分器(TD)为ω*提供过渡过程,通过TD 对噪声具有很好的滤波作用,获得光滑的跟踪信号v1,并提取其一次微分信号v2,滑模扩张状态观测器给出对象状态变量的估计值z1、z2以及系统扰动的实时作用量的估计z3,而的反馈用来补偿扰动,这是一个具有自动补偿系统扰动的反馈结构。实际中,补偿 控制量,u0(t)为运行过程中uq的控制量,用状态误差e1、e2和e0的非 线性状态反馈,将非线性控制系统转化为积分器串联型的线性控制系统,确定跟踪设定值的控制量,用式(14)的滑模非线性状态误差反馈控制律进行控制实现滑模自抗扰控制。
3.2 基于滑模自抗扰控制的直轴电流环调节器
对于交流永磁同步电动机的d 轴电流环,本文设计了一阶滑模自抗扰控制器来对其控制。
由式(1)可知,将iq对d 轴电流环的耦合作用视为d 轴电流环的扰动量a2(t),即

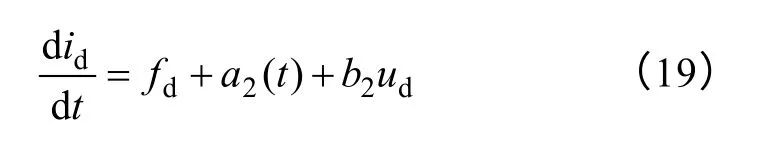
式中,fd为系统已知扰动;a2(t)为系统外部未知扰动量。通过这两项可以有效地估计电流环的扰动,并对此扰动进行补偿,对输入电压扰动有很好的抗扰性。
与速度电流环控制器设计相类似,只是将二阶控制器降为一阶控制器,这样调节器参数更少,调试更方便,系统更稳定。由一阶线性跟踪器微分及式(8)、式(11)和式(19)便可得到d 轴电流环的滑模自抗扰控制器,其控制结构如图3所示。用其来控制d 轴电流,不仅能获得良好的动态性能,还能对系统电压扰动进行估计并补偿,使得系统的稳定性更好。
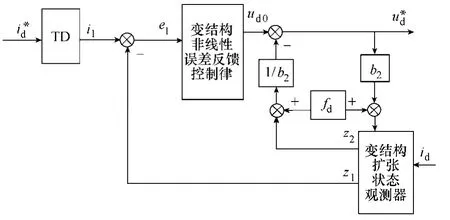
图3 d 轴电流环的变结构自抗扰控制结构Fig.3 d-axis current loop VS-ADRC control structure
PMSM 滑模自抗扰速度控制系统结构如图4所示,通过跟踪微分器安排过渡过程并给出此过程的微分信号,使得系统响应迅速且无超调;通过滑模扩张状态观测器作用,不但能获得各状态变量的观测值,且能得到系统扰动的观测值。比如:转动惯量和定子电阻、电感变化带来的扰动以及负载扰动等其他外部未知扰动;通过滑模非线性状态误差反馈控制律,不但可以对各种扰动进行补偿,而且能对速度和电流信号实现“小误差大增益,大误差小增益”的非线性控制。对典型自抗扰控制器的改进使得滑模自抗扰控制器在很大范围内能够达到最优控制,改进后的控制器既保持了原有特点又减少了可调参数,并改善了系统的鲁棒性和对系统外部的抗扰动性,提高了PMSM 速度控制系统的稳态准确度和速度控制性能,并且能够克服滑模控制系统抖振的问题。
该系统采用id=0 的双闭环矢量控制结构,即速度环和电流环。速度电流环是将速度环、电流环综合在一起而形成的一种新的速度电流环滑模自抗扰控制器。d 轴电流环同样使用改进后的调节器,与典型的控制结构相比,不仅减少了控制环节,优化了控制策略,而且增强了整个控制系统抗扰动性能,提高了系统稳定性。
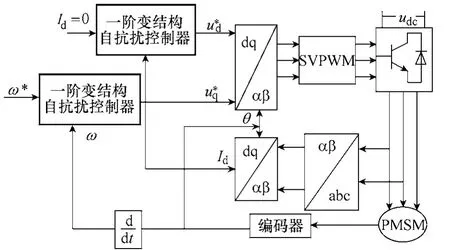
图4 PMSM 滑模自抗扰速度控制系统结构图Fig.4 VS-ADRC for PMSM control system structure
4 仿真及实验结果分析
为验证滑模变结构自抗扰控制器的永磁同步电动机控制系统的性能,本文利用Matlab/Simulink 对控制系统实现了数字仿真,在与实验条件相同的条件下,以自主研发的变频调速控制系统为核心对一台自主研发的交流永磁同步电动机采用典型的自抗扰和滑模变结构自抗扰控制策略分别进行控制。交流永磁同步电动机参数如下:额定功率PN=11.3kW,额定转速n=6 000r/min,定子电阻R=0.506Ω,交轴、直轴分别为Ld=Lq=7.638 5mH,转动惯量为J=50.2kg·cm2,极对数p=2,额定转矩Te=18N·m,转子磁通φ0=0.812T,额定频率fN=200Hz。
在实际中,需对控制器各部分的参数进行整定,经反复调试,速度电流环中,TD 中的参数确定后保持不变速度因子取r=106,变结构扩张状态观测器和变结构非线性状态误差反馈控制律中的参数取δ1=0.05,δ2=0.025,k=30,l=25;电流环中的参数取为:r=103,δ1=0.03,δ2=0.015,k=10,l=5。
图5为ADRC 和VS-ADRC 两系统的低转速响应波形,当转速n=20r/min时,在2s时刻,转矩从0.334N·m 上升至18N·m,由图可知,在低速时,滑模自抗扰控制系统与典型自抗扰控制系统相比,具有更好的启动特性和系统鲁棒性。
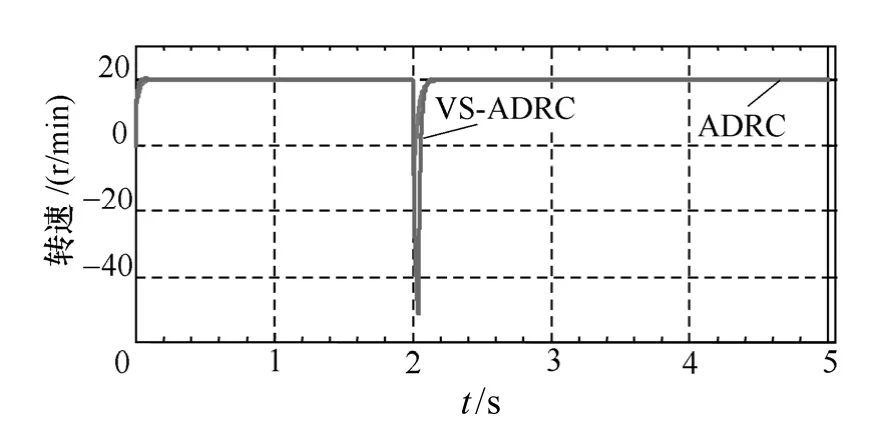
图5 低速响应波形对比Fig.5 System response comparison waveforms at low speed
图6为典型自抗扰和滑模自抗扰两系统的高转速响应波形,当转速n=6 000r/min时,在2s时刻,转矩从0.334N·m 上升至18N·m,从图中可以看出,高速时,滑模自抗扰系统的动静态性能、抗扰动能力和转速控制准确度均优于典型自抗扰控制系统,而且具有良好的自适应能力。
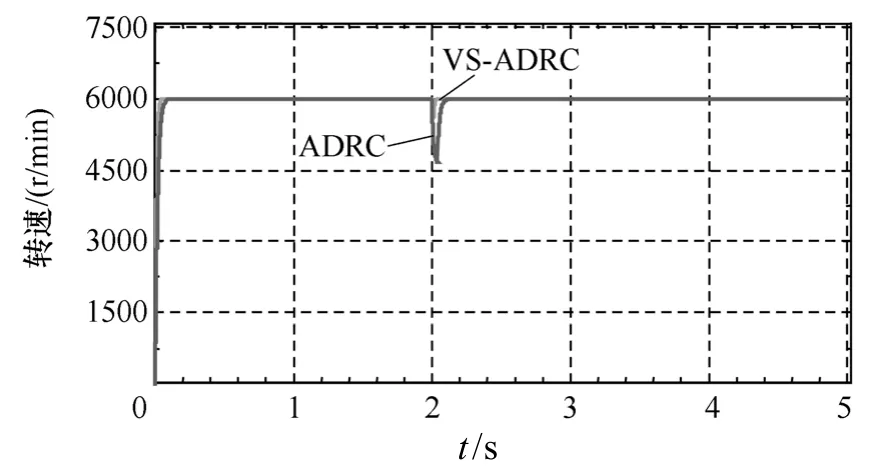
图6 高速响应波形对比Fig.6 System response comparison waveforms at high speed
图7为典型自抗扰和滑模变结构自抗扰两系统的电磁转矩响应曲线,由图可知,在电动机启动时,滑模自抗扰控制系统的电磁转矩脉动明显小于典型自抗扰控制系统的电磁转矩脉动,且稳态时,几乎没有转矩脉动。在2s时,滑模变结构自抗扰控制系统电磁转矩响应迅速且能很好地跟踪给定值,从而降低了系统损耗,减少了系统所受到的电磁干扰和负载转矩扰动,有利于提高系统控制性能。
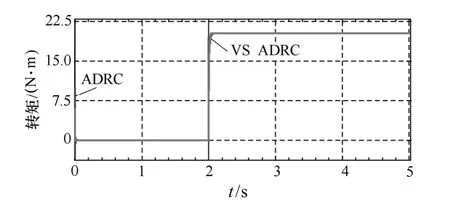
图7 电磁转矩响应曲线对比Fig.7 Electromagnetic torque waveforms comparison
在PMSM 速度控制系统中,根据实际的应用情况,对ADRC 和VS-ADRC 两种控制策略在同一特定情况下,例如给定转速及转动惯量发生变化,给定波形按方波、正弦波进行运行,可以体现出VS- ADRC 更好的的实用价值。
当系统转动惯量由1.48×10-2kg·m2变为7.4×10-3kg·m2时,从图8中可以明显地看出VS-ADRC控制策略的优越性,系统在给定转速200r/min 的情况下,空载起动电动机。采用VS-ADRC 控制时,超调量相比ADRC 要小很多,由此可知VS-ADRC抗扰动能力要远远强于ADRC,真正体现了VS-ADRC不受外部扰动的变化,且能更好地实时补偿扰动的能力,有更优良的系统鲁棒性。
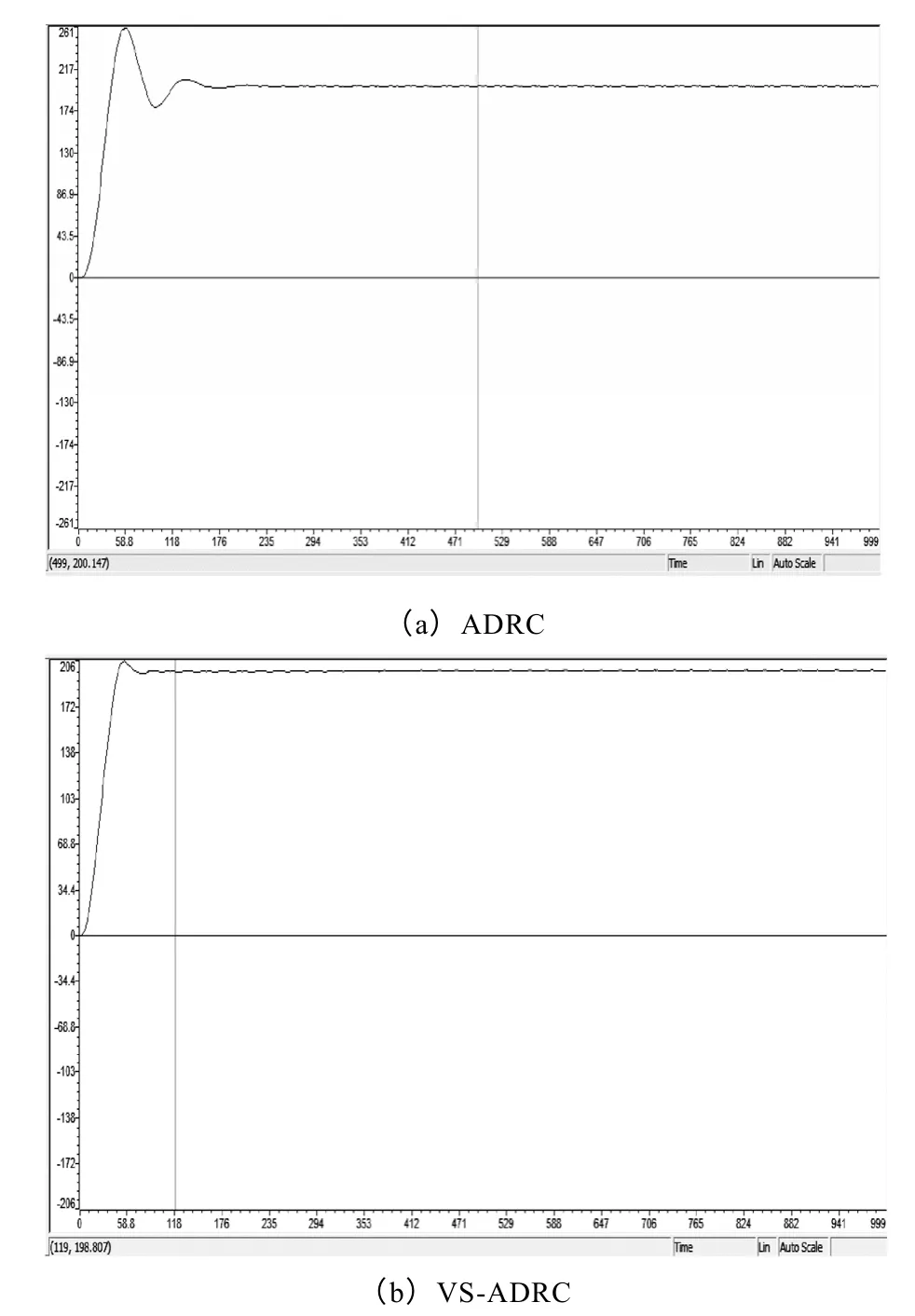
图8 给定转速200r/min时VS-ADRC 与ADRC 的 转速实验波形对比Fig.8 Experimental waveform comparison of the speed of VS-ADRC and ADRC at 200r/min
当系统转动惯量由1.48×10-2kg·m2变为7.4×10-3kg·m2时,速度给定为-200~+200r/min 的正弦波,周期为4s。从图9可以明显看出,ADRC 的速度波形出现振荡,偏差较大;相比之下,VS-ADRC有着优良的跟随性能,在快速性和稳定性中的优势明显,因此仍然能够很好地完成速度控制,具有很好应用价值的。
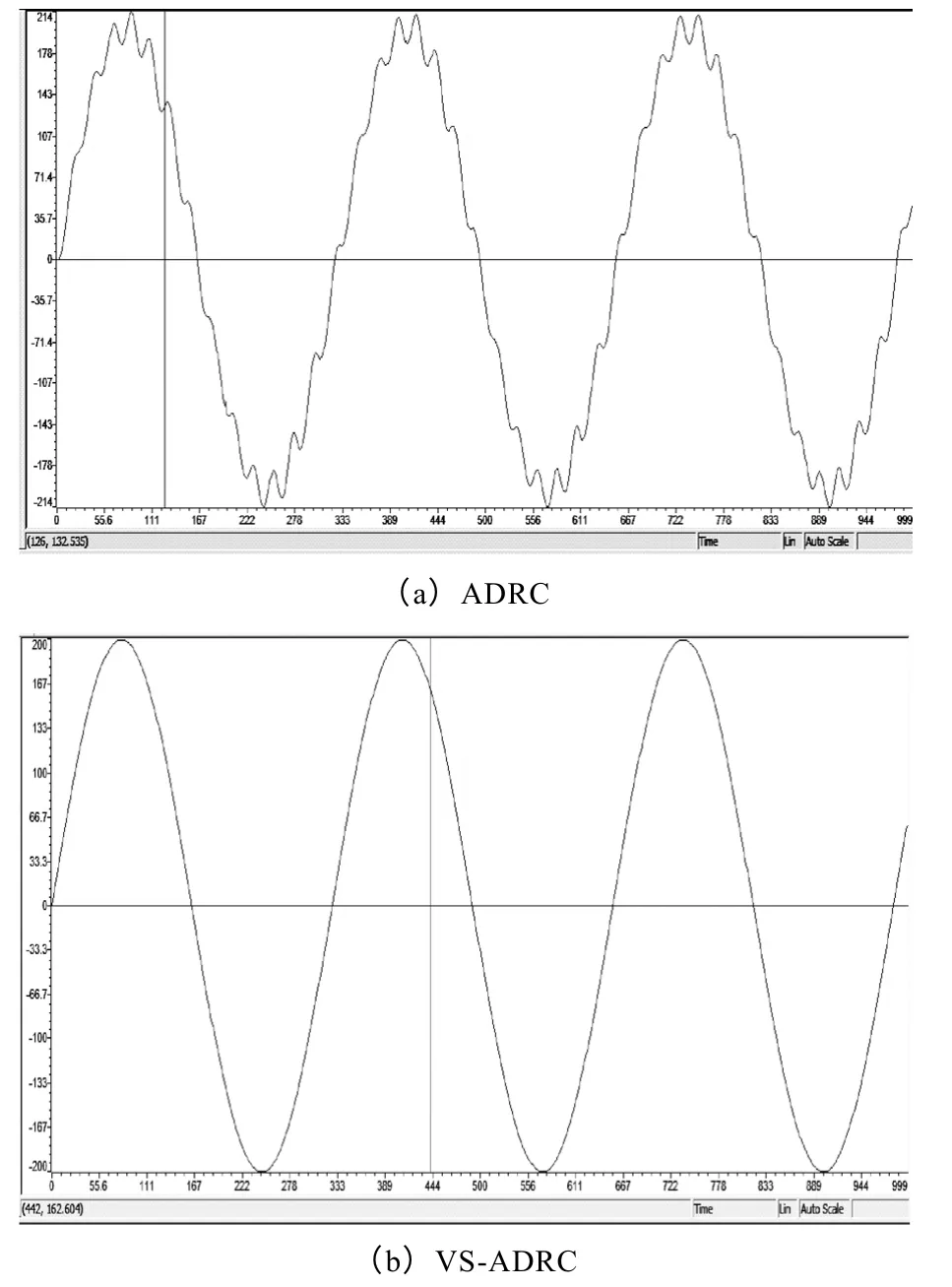
图9 速度给定为-200~+200r/min 的正弦波,VS-ADRC 与ADRC 的实验波形对比Fig.9 Experimental waveform comparison of the speed of VS-ADRC and ADRC at -200~+200r/min
同样,以方波为例,当系统转动惯量由1.48×10-2kg·m2变为 7.4×10-3kg·m2时,速度给定为-200~+200r/min 的方波,周期为4s。从图10可以明显看出,ADRC 控制器速度波形出现较大超调,调整时间变长,并有振荡出现;相比之下,VS-ADRC速度波形转速超调明显减小,速度响应速度变快,跟随性能提高。
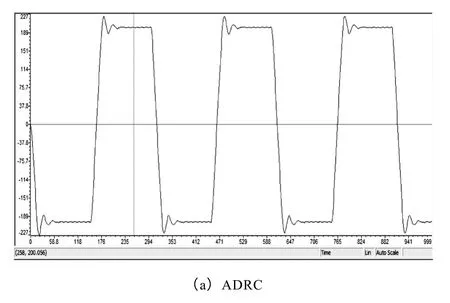
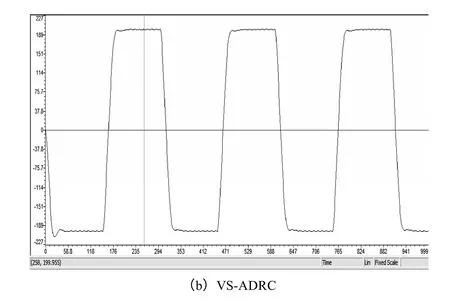
图10 速度给定为-200~+200r/min 的方波,VS-ADRC 与ADRC 的转速实验波形对比Fig.10 Experimental waveform comparison of the speed of VS-ADRC and ADRC at -200~+200r/min
5 结论
本文根据实际需要,将滑模变结构自抗扰控制理论应用于高性能交流永磁电动机速度控制系统,设计出速度电流环的二阶滑模变结构自抗扰控制器,以增强系统的抗扰动的能力。通过对直轴电流输出方程的分析,提出了一种新的电流环滑模自抗扰控制方案,在保证系统动态性能的同时,提高了系统鲁棒性。仿真与实验表明,采用滑模自抗扰控制的PMSM 调速系统具有良好的动、静态性能,此系统实现了高性能变频调速,减少了可调参数,克服了滑模控制抖振的缺陷,速度控制系统对形成的总扰动具有较强的鲁棒性,并且实现了滑模自抗扰控制技术运用于高性能的伺服控制领域。
[1]Liu Da,Li Muguo.Adaptive predictive control system with disturbance compensation based on self-recurrent wavelet neural network[J].International Journal of Advancements in Computing Technology,2011,3(10):330-338.
[2]Dogan M,Dursun M.Application of speed control of permanent magnet synchronous machine with PID and fuzzy logic controller[J].Energy Education Science and Technology Part A:Energy Science and Research,2012,28(2):925-930.
[3]Xia Cunjian,Wang Xiaocui,Li Shihua,et al.Improved integral sliding mode control methods for speed control of PMSM system[J].International Journal of Innovative Computing,Information and Control,2011,7(4):1971-1982.
[4]Su Y X,Zheng C H,Duan B Y.Automatic disturbances rejection controller for precise motion control of perma- nent-magnet synchronous motors[J].IEEE Transac- tions on Industrial Electronics,2005,52(3):814-823.
[5]Wang Xiaocui,Li Shihua,Chen Xisong,et al.Improved integral sliding mode control methods for speed control of PMSM system[J].International Journal of Innovative Computing,Information and Control,2011,7(4):1971-1982.
[6]朱玉川,李志刚,马大为,等.永磁交流位置伺服系统串级复合滑模控制[J].系统仿真学报,2007,19(12):2779-2782.
Zhu Yuchuan,Li Zhigang,Ma Dawei,et al.Cascaded compound sliding-mode control for permanent magnet synchronous motor position servo system[J].Journal of System Simulation,2007,19(12):2779-2782.
[7]Vu T T,Yu D Y,Han H C,et al.T-S fuzzy-model- based sliding-mode control for surface-mounted permanent-magnet synchronous motors considering uncertainties[J].IEEE Transactions on Industrial electronics,2013,60(10):4281-4291.
[8]Rong Jong Wai,Kuo Ho Su.Adaptive enhanced fuzzy sliding-mode control for electrical servo drive[J].IEEE Transactions on Industrial Electronics,2006,53(2):569-580.
[9]韩京清.自抗扰控制技术—估计补偿不确定因素的控制技术[M].北京:国防工业出版社,2008.
[10]卢达,赵光宙,曲轶龙,等.永磁同步电机无参数整定自抗扰控制器[J].电工技术学报,2008,28(3):27-34.
Lu Da,Zhao Guangzhou,Qu Yilong,et al.Permanent magnet synchronous motor control system based on no manual tuned active disturbance rejection control[J].Transactions of China Electrotechnical Society,2008,28(3):27-34.
[11]陈洪,高延滨,孙华.自适应模糊自抗扰控制器的研究与设计[J].控制系统,2008,24(8):32-33. Chen Hong,Gao Yanbin,Sun Hua.The design and research of fuzzy self-adapted ADRC arithmetic[J].Control System,2008,24(8):32-33.
[12]Huang Shoudao,Kuang Jiangchuan,Huang Qing,et al.IPMSM sensorless control based on fuzzy active- disturbance rejection controller for electric vehicle[C].Power Engineering,Energy and Electrical DrivesInternational Conference 2011:1-6.
[13]Li Shihua,Liu Zhizhang.Adaptive speed control for permanent magnet synchronous motor system with variations of load inertia[J].IEEE Transactions Industrial Electronics,2009,56(8):3050-3059.
[14]孙凯,许镇琳,盖廓,等.基于自抗扰控制器的永磁同步电机位置伺服系统[J].中国电机工程学报,2007,27(15):43-46.
Sun Kai,Xu Zhenlin,Gai Kuo,et al.A novel position controller of PMSM servo system based on active- disturbance rejection controller[J].Proceedings of the CSEE,2007,27(15):43-46.
[15]邵立伟,廖晓钟,张宇河,等.自抗扰控制在永磁同步电机无速度传感器调速系统的应用[J].电工技术学报,2006,21(6):35-39.
Shao Liwei,Liao Xiaozhong,Zhang Yuhe,et al.Application of active disturbance rejection controller and extend state observer for PMSM[J].Transactions of China Electrotechnical Society,2007,21(6):35-39.
[16]Liu Huixian,Li Shihua.Speed control for PMSM servo system using predictive functional control and extended state observer[J].IEEE Transactions on Industrial Electronics,2012,59(2):1171-1183.
