一种基于线电感变化特征的永磁同步电机转子初始位置检测新方法

孟高军 余海涛 黄 磊 酒晨霄 赵东东

（1.东南大学伺服控制技术教育部工程研究中心 南京 210096 2.飞行器控制一体化技术重点实验室 西安 710000）

0 引言

永磁同步电机（Permanent Magnet Synchronous Motors，PMSM）具有功率因素高、过载能力强以及输出转矩能力强等优点，在家用电器、船舶推进、及电动车驱动等领域得到了广泛的应用[1]。而能否对转子初始位置进行准确估计是永磁同步电机高性能控制策略（矢量控制或直接转矩）和无位置传感器运行实现的前提条件，也是关系到电机是否顺利起动，以及能否实现最大转矩起动的关键问题，一直是工程技术界研究的热点和难点问题之一。

因此国内外学者对永磁同步电机转子初始位置检测展开了大量的研究。文献[2-7]根据脉冲信号检测的方法向电机中注入幅值相同、方向不同的一系列电压脉冲，检测并比较响应电流的大小来估计转子初始位置。这种方法可行，但如果想得到准确的转子初始位置需要施加多个不同方向的电压矢量，对逆变器的控制较为复杂。文献[8-15]是采用高频信号注入法，其基本原理是在电机中注入特定的高频电压信号，然后检测电机中对应的电流信号以确定转子的初始位置，但该方法算法较为复杂，且需要低通滤波器等额外的硬件电路，增加了成本。文献[16]提出了一种通过向电机定子侧施加低频旋转电压矢量来检测转子初始位置的方法，但是产生的电流后续处理较为复杂，且会造成较大的转矩脉动。文献[17]提出了一种基于相电感线性区模型的初始位置检测方法，该方法中相电感模型简单，利用电感估计值可以实现静止时的初始定位，但该方法需要预先测量各相电感曲线交点位置处的电感值，不具备动态适应性，且只适用于功率变换器为不对称半桥结构的开关磁阻电机。文献[18]利用定子电感值随转子位置改变呈正弦变化的规律，在电机运行前，检测定子绕组的电流和电压，计算此时的电感值，该方法原理较简单，但对电感值的测量较为复杂，计算误差较大，且需要占用一定的存储器空间。文献[19,20]比较施加正反电压矢量过程中非导通相的端电压，然后比较定子电流的峰值，最终得到转子初始位置估计准确度为30°，该方法不仅估计准确度低，而且需要端电压采集电路，增加了系统的复杂性。

针对以上方法存在的不足，本文从凸极效应对绕组电感的影响出发，在验证其线电感呈正弦分布且一个周期变动两次的基础上，提出了一种用于转子初始位置检测的新方法。首先，通过注入高频低压脉冲来进行线电感辨识，并利用辨识出的线电感信息和转子位置关系，经旋转坐标变换初步计算转子位置角，随后再结合铁心非线性磁化特性判断转子磁极极性，最后搭建了AD5435 实时仿真系统平台，对该方法的有效性和正确性进行了实验验证，并给出了相应的结论。

1 永磁同步电机绕组电感随转子位置的变化规律

对于永磁同步电机而言，绕组电感的大小随转子位置改变而呈现一定规律的变化[21]，假设电机三相绕组对称，如图1所示，当θr=0°和180°时，a 相绕组轴线与转子的d 轴重合，此时绕组的主磁通由空间气隙以及定、转子铁心组成；当θr=90°和270°时，a 相绕组轴线与转子的q 轴重合，此时原磁路中的转子铁心被同体积的转子永磁磁极取代；由于铁心磁导率大于永磁体的磁导率，故当θr=0°和180°时，a 相自感最大，θr=90°和270°时，a 相自感最小。同理，当θr=−30°和150°时，ab 相互感最大，当θr=60°和240°时，ab 相互感最小。

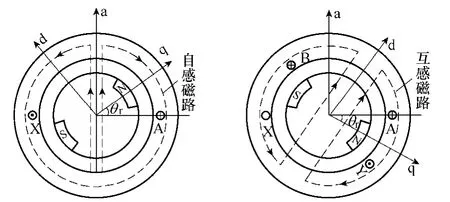
图1 凸极效应对绕组自感和互感的影响Fig.1 Saliency effect from rotor to winding self-inductance and mutual-inductance

至此，在不计3 次及以上谐波的情况下，三相PMSM 在定子坐标系下的电感可以表示为[22]

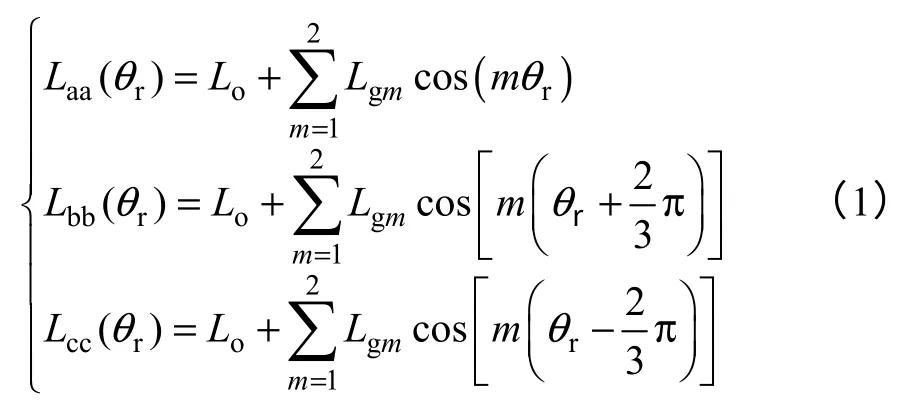
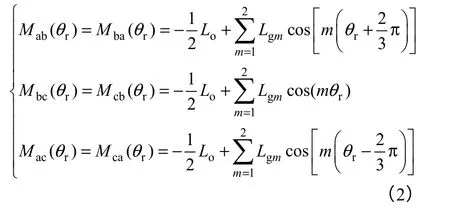
式中，θr转子电角度；Laa、Lbb和Lcc为三相绕组自感；Mab、Mbc和Mac为三相绕组互感；Lo为绕组自感的恒定分量；Lgm为自感的m次谐波幅值。

1.1 线电感辨识新方法

为测量线电感采取功率管两两导通的控制方式，每一刻电机有两相导通，非导通相悬空，如图2所示。Ud为直流母线电压；N 为中性点；VT1～VT6为功率驱动器件；VD1～VD6为二极管。具体的操作过程如下。

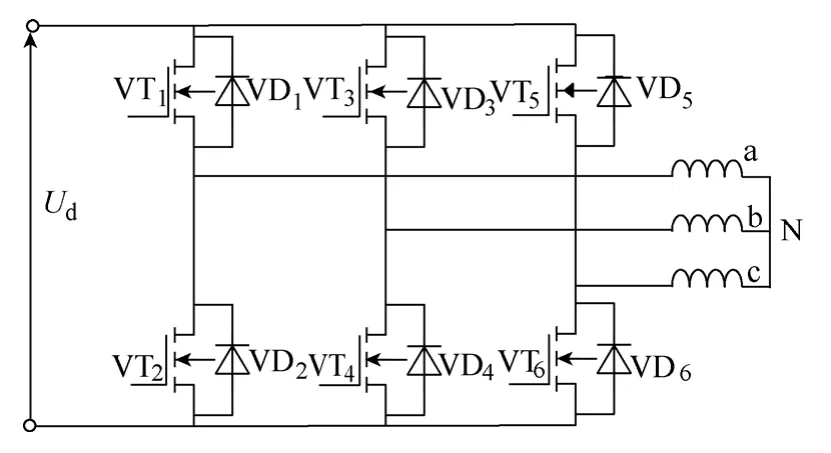
图2 三相全桥式永磁同步电机驱动结构Fig.2 Diagram of three-phase full-bridge PMSM drive circuit

如图3所示，以施加电压脉冲到a、b 相，VT1、VT4导通，C 相悬空为例，计算线电感Lab，令

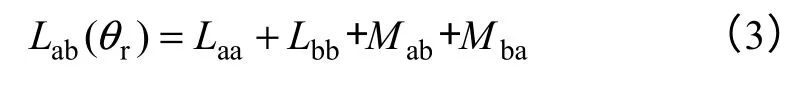
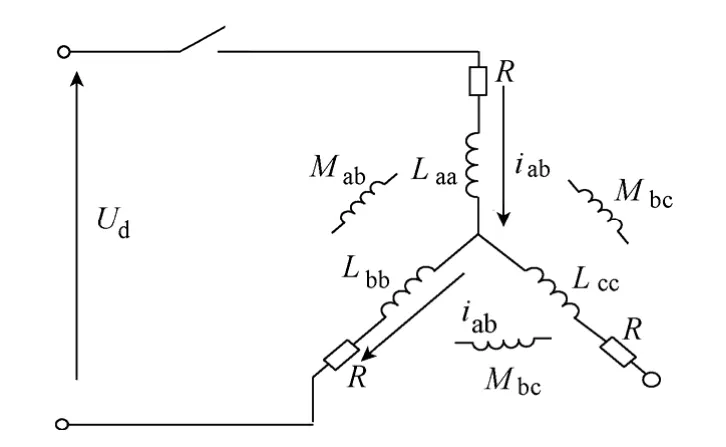
图3 a、b 相导通时的等效电路Fig.3 Equivalent circuit of motor during phase a and b are conducting

当使VT1和VT4导通，其他功率管关断时

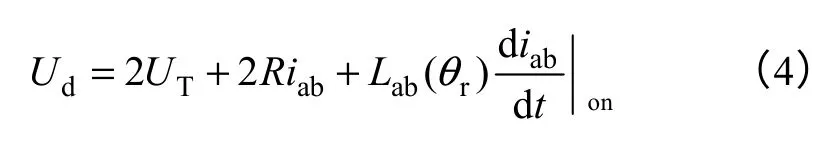
如当VT1和VT4关断时，电流通过二极管（VD2、VD3）续流，电压方程表示为

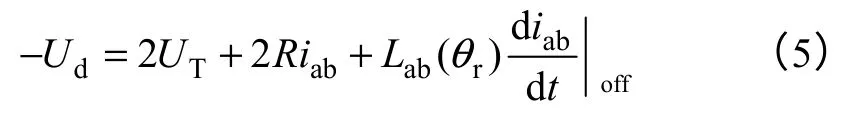
式中，Ud为直流母线电压；UT为功率器件导通时的 管压降；R为每相绕组电阻；为电流的上升斜率；为电流的下降斜率。

上述过程其实质为RL 电路的电流响应，如图4所示。由于功率管从开通到关断的时间间隔很短，尽管线电流的瞬时值并不相同，但是它们的平均值几乎相同。因此，可以假设此时式（4）、式（5）中功率管压降UT和绕组电阻压降在功率管开关状态改变区间的平均值分别都是相等的，那么可以得到

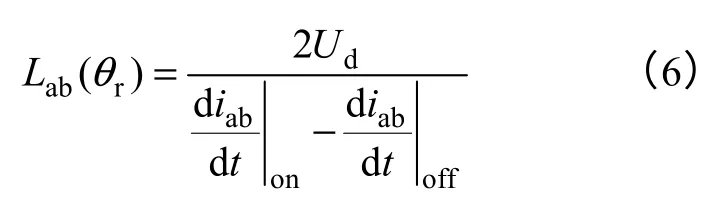
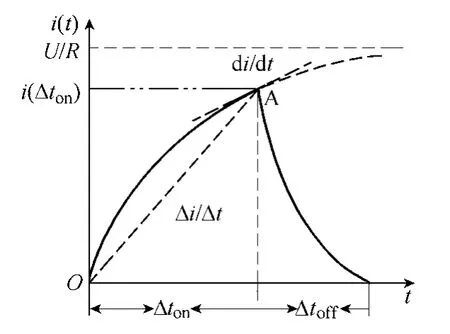
图4 全桥驱动的零状态电流响应Fig.4 Current zero-state response of RL circuit

由式（6）可以看出，在直流母线电压给定的情况下，线电感的大小与线电流上升和下降斜率差成反比，即该测量方法必须准确地检测线电流的上升和下降斜率。

在实际应用中，微处理器的AD 采样为离散方式，即每隔一定的采样时间Δt才能获得1 次电流信号，其采样值为Δi。从图4中可以看出，采样点A处的瞬时电流变化率di/dt和平均电流变化Δi/Δt不相等，可以分别表示为[19]

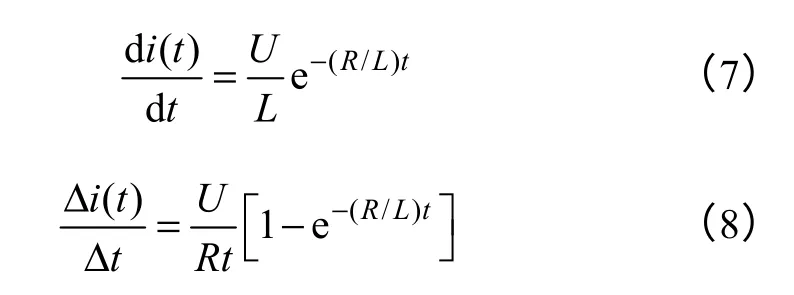
定义平均电流变化率和瞬间电流变化率之比为斜率误差系数，即

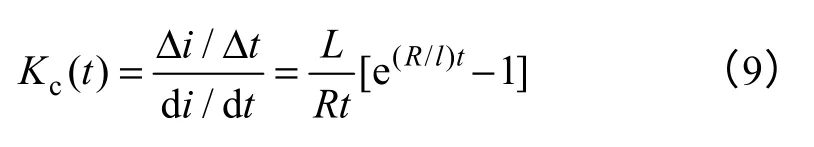
假设电流采样时间很短。对式（9）泰勒级数展开并略去高次项，其比值接近于1，如式（10）所示

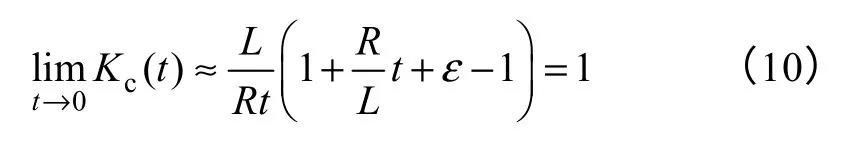
通过式（9）和式（10）可以看出，功率管导通时间越短，其电流上升阶段的电流瞬时变化率和电流平均变化率越接近，因此缩短电压脉冲持续时间，同时将检测到的电流峰值i(Δton)作为电流响应的变化量，引入电流平均变化率并代入式（6），线电感计算公式可以表示为

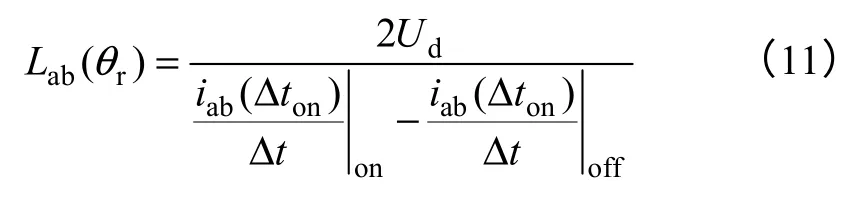
这种检测方法间接消除了定子电阻和功率管压降的影响，可以有效提高电感辨识准确度。

1.2 绕组电流对线电感的影响

根据式（1）～式（3）可得

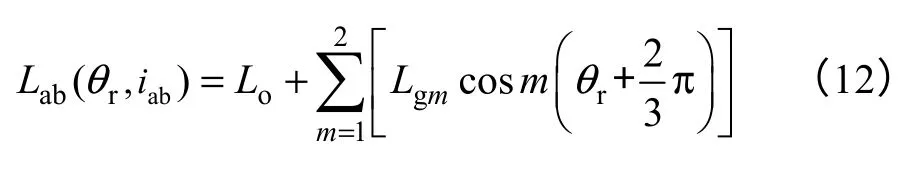
为了深入分析绕组电流对线电感的影响，对一台2 对极三相永磁同步电机（样机）的线电感Lab进行测量，电机转子为凸极结构。

图5为Lab(θr,iab)的实测曲线，用傅里叶级数分解的结果表明，二次以上谐波的幅值都很小，可以不计。分解到Lo、Lg1和Lg2的值如图6曲线所示。曲线表明了其与iab的函数关系。可以看出，在一定 电流范围内可以用iab或的线性关系来表示，即

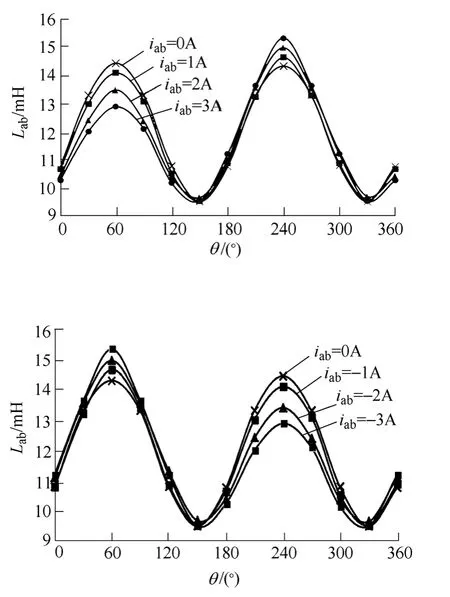
图5 Lab(θr,iab)实测曲线Fig.5 Samples of measuredLab(θr,iab)curves

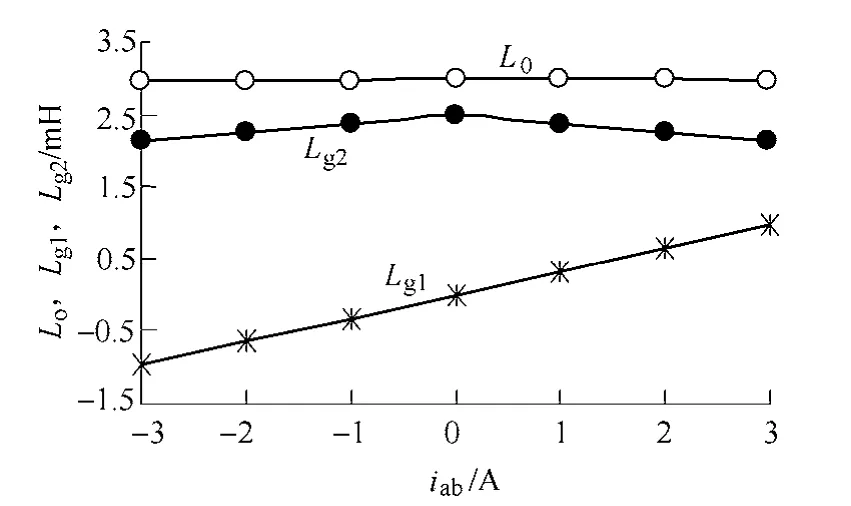
图6 Lo,Lg1,Lg2=f(iab)实测曲线Fig.6 Samples of measuredLo,Lg1,Lg2=f(iab)curves

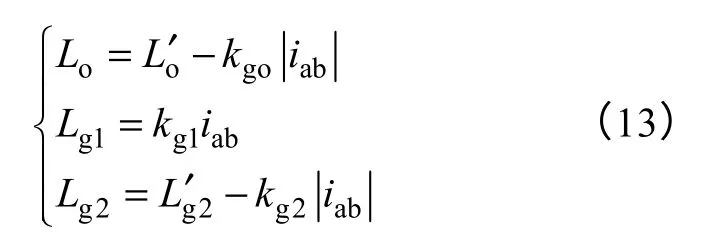
由图5和图6可以看出绕组电流对线电感测量的影响，这是由于永磁磁动势与绕组磁动势共同作用，影响绕组磁路的饱和度及电感值，且这种影响随转角位置不同而变化。故为了避免因增磁和去磁给电感值辨识带来的误差，在上述1.1 节的操作过程中，应尽可能地缩短电压脉冲施加时间以便达到降低电流响应峰值的目的。

1.3 转子位置初始估计

结合图6和式（13）可知，当绕组电流值在区间[−1,1]时，线电感值可近似表示为

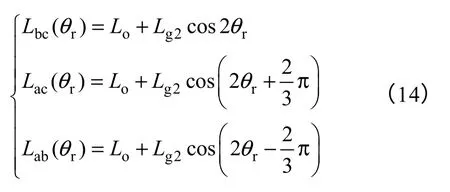
根据线电感Lab、Lac和Lbc大小的变化规律可以将每个电周期的线电感分为12 个区间，如图7所示。其中每个区间的线电感大小比较见表1。

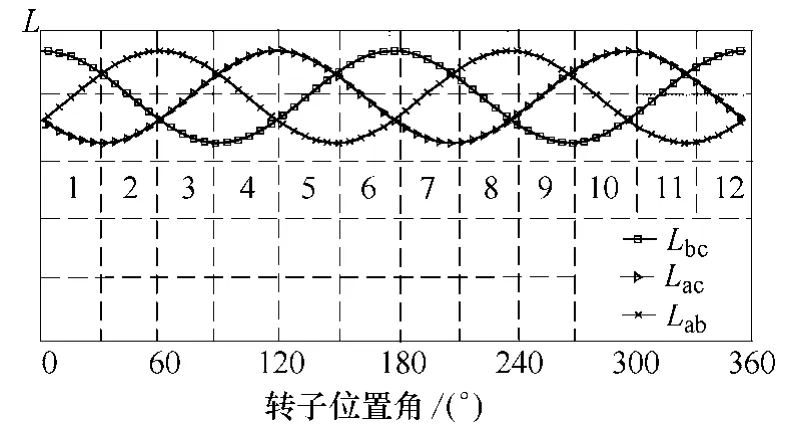
图7 PMSM 线电感分区原理图Fig.7 Principle diagram of line inductance subregion

表1 线电感正弦区选择逻辑Tab.1 Chosen logics of line inductance

据电机坐标变换基本理论，静止坐标系abc 与旋转坐标系αβ 之间的关系可以表示为

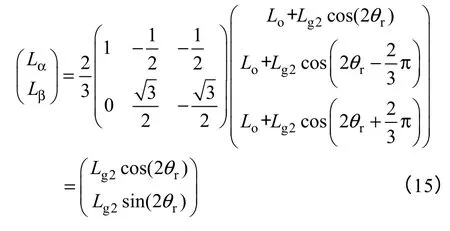
那么，θr可以表示为

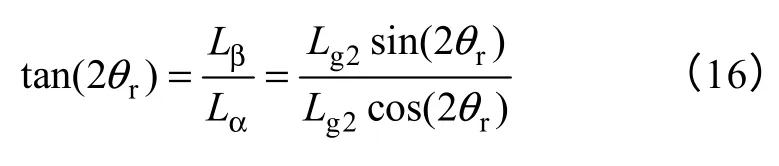
通过式（16）和表1，可以得到转子位置角为

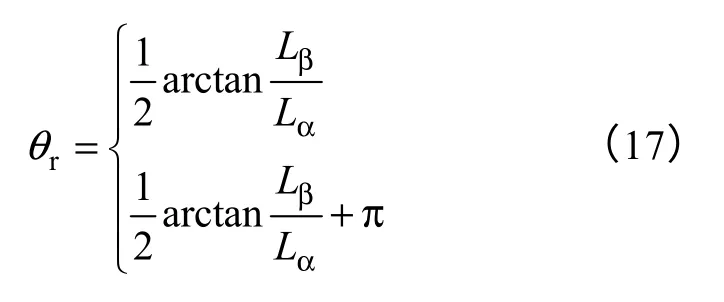
1.4 转子磁极极性判断

虽然式（17）结合表1 可以提取出转子的位置信息，但由于区间1～6 和区间7～12 的电感变化规律一致，故所得的两个转子位置角相差180°，即假如Lbc＞Lab≥Lac，转子位置角位于0°～30°或180°～210°。

因此本文加入N/S 极性判定步骤。此步骤是利用铁心的饱和效应来完成，原理如下：设定S=0 表示下桥臂导通，S=1 表示上桥臂导通，如S(abc)=100表示a 相上桥臂导通，b 和c 相下桥臂导通。

由图8a 可以看出，当转子N 极位于0°～60°时，向逆变器施加（101）的脉冲信号，则绕组的合成磁动势与转子磁动势同向，磁场增强，磁路更加饱和，由于铁心磁化曲线的非线性特性，使磁导率减小，b 相电感值减小，则电流响应速度加快。当向逆变器施加（010）的脉冲信号时，如图8b 所示，若转子N 极仍位于0°～60°，则定、转子磁动势反向削弱，b 相绕组自感增大，电流响应的速度减慢。因此，当施加（101）和（010）的电压脉冲宽度相同时，电流响应的峰值。反之当转子N 极位于180°～240°时，电压响应的峰值为。具体等宽电压脉冲方法分配如图9所示。电流检测规则见表2。

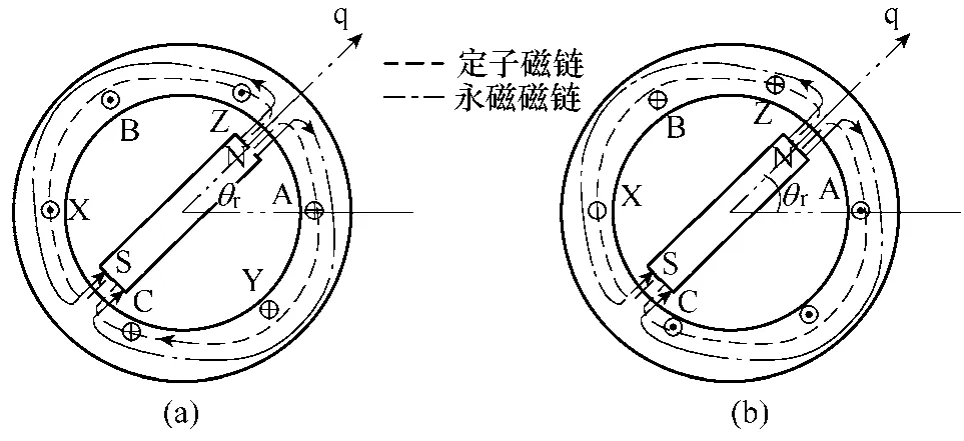
图8 定子磁链和永磁体磁链方向示意图Fig.8 Direction of stator flux and permanent magnetic flux

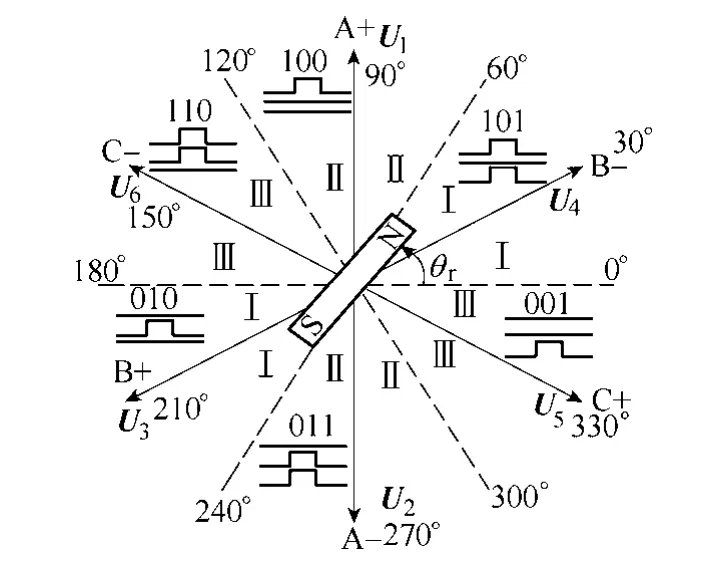
图9 电压脉冲矢量与转子空间位置区域Fig.9 Applied voltage vectors and rotor position areas

表2 等宽电压脉冲法实施规则Tab.2 The method of identical voltage pulses

2 实验结果与分析

2.1 实验系统和流程介绍

以一台 2 对极的三相永磁同步电机为实验对象，电机参数见表3，同时采用三菱公司的电压源型逆变器（IPM）提供脉冲电压，通过LCR 数字电桥检测线电感实际值，以A&D 实时仿真装置为控制中心来对转子初始位置进行估计。具体实施流程如图10所示，实验系统实物如图11所示。

表3 永磁同步电机（样机）参数Tab.3 Parameters of PMSM

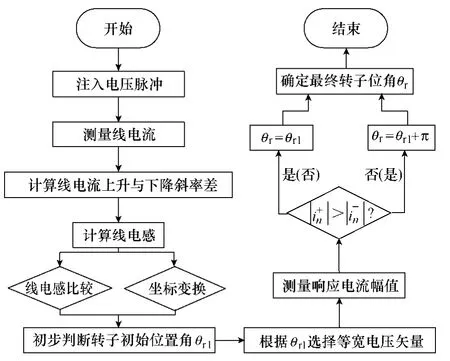
图10 实施流程Fig.10 Flowchart of control scheme implementation

图11 永磁同步电机实验系统实物图Fig.11 Picture of actual PMSM experiment system

由于线电感计算准确度直接影响位置估算精度，为避免绕组电流对线电感的影响，同时考虑到电流传感器的采样准确度及斜率误差系数。首先需要选择最优电压脉冲施加时间Δton，结合本文的理论分析由图12可以看出，当Ud=16V，Δton=1ms时，响应电流峰值imax=0.8A，符合线电感辨识准确度要求。因此本实验中，每个电压矢量施加的时间为Tc（1ms），两个电压矢量施加的时间相隔2ms，注入电压幅值为16V，在第二步检测转子磁极方向的过程中，为了达到磁饱和的效果且便于两个电流峰值的比较，因此施加的等宽电压脉冲时间延长为TL（4ms），电压脉冲的时间相隔8ms。

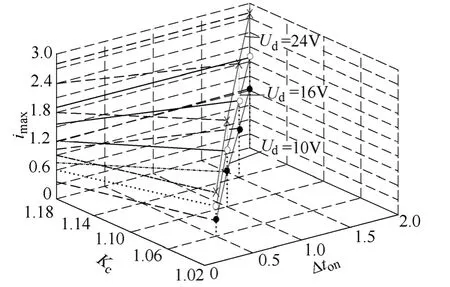
图12 Kc、Δton、Ud和imax关系图Fig.12 Relation schema ofKc、Δton、Udandimax

2.2 线电感检测

本文所提出的线电感计算方法首先通过求解线电流上升和下降斜率差，得到电流斜率差值，再利用式（11）即可得到各线电感值。为了验证本文提出的线电感计算方法的准确度，图13比较了通过新方法计算的ab 线电感值和用数字电桥实测的ab 线电感值，可见两者吻合程度较好，证明了此方法的准确性。

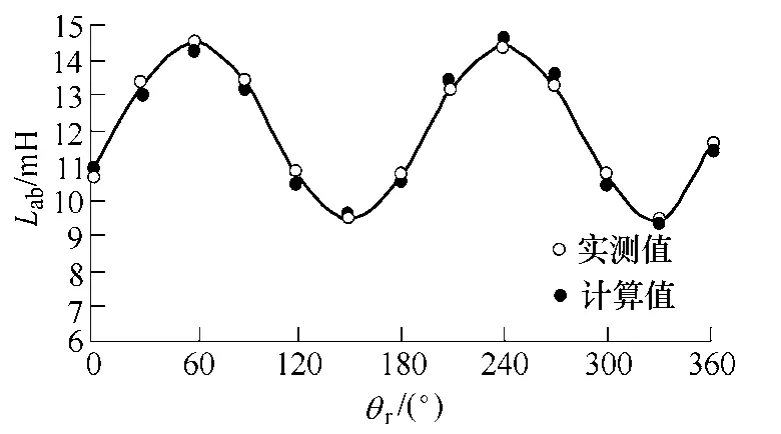
图13 线电感实测和计算比较Fig.13 Comparison of line inductance measured and calculation

2.3 PMSM 电机的初始位置估计

图14a 和14b分别为向电机施加时间为Tc和TL的电压脉冲后的转子位置响应图，可以看出在整个检测过程中，电机位置仅发生较小的波动现象，不影响整个实验过程。

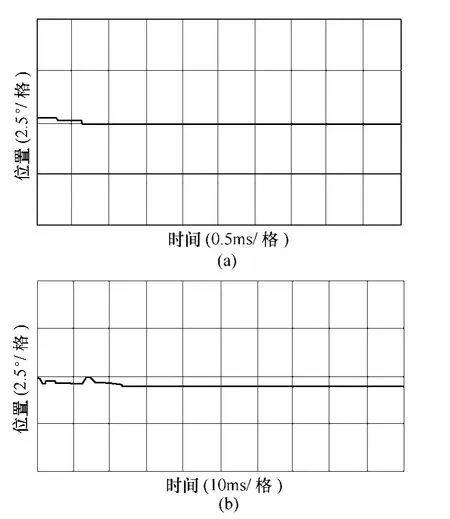
图14 施加电压脉冲时的转子位置响应Fig.14 Position responses at standstill

转子初始位置在45°时，首先检测ab、bc 和ca绕组的线电流值，经计算得出相应线电感值，同时结合表1 和式（17）可初步判断转子初始位置估计值θr1=228°或者θr1=48°，如图15a 所示。下一步采用等宽电压脉冲的方法确定转子磁极正方向，依照表2 的实施规则，进行转子磁极方向判断，结果如图 15b 所示，可以看出，，再结合初次估算值得出转子初始位置估计值θr=228°，误差为3°。

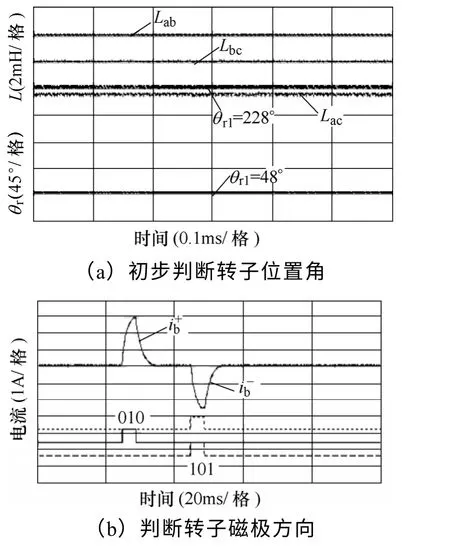
图15 转子初始位置在225°时的实验波形Fig.15 Experimental waveforms of rotor initial position on 225°

转子初始位置在150°时，按同样的方法，可初步确定转子初始位置估计值θr1=152°或者θr1=332°，如图16a 所示。下一步采用等宽电压脉冲的方法确定转子磁极的正方向，结果如图16b 所示，明显可 以看出，，再结合初次估算值得出转子初 始位置估计值θr=152°，误差为2°。

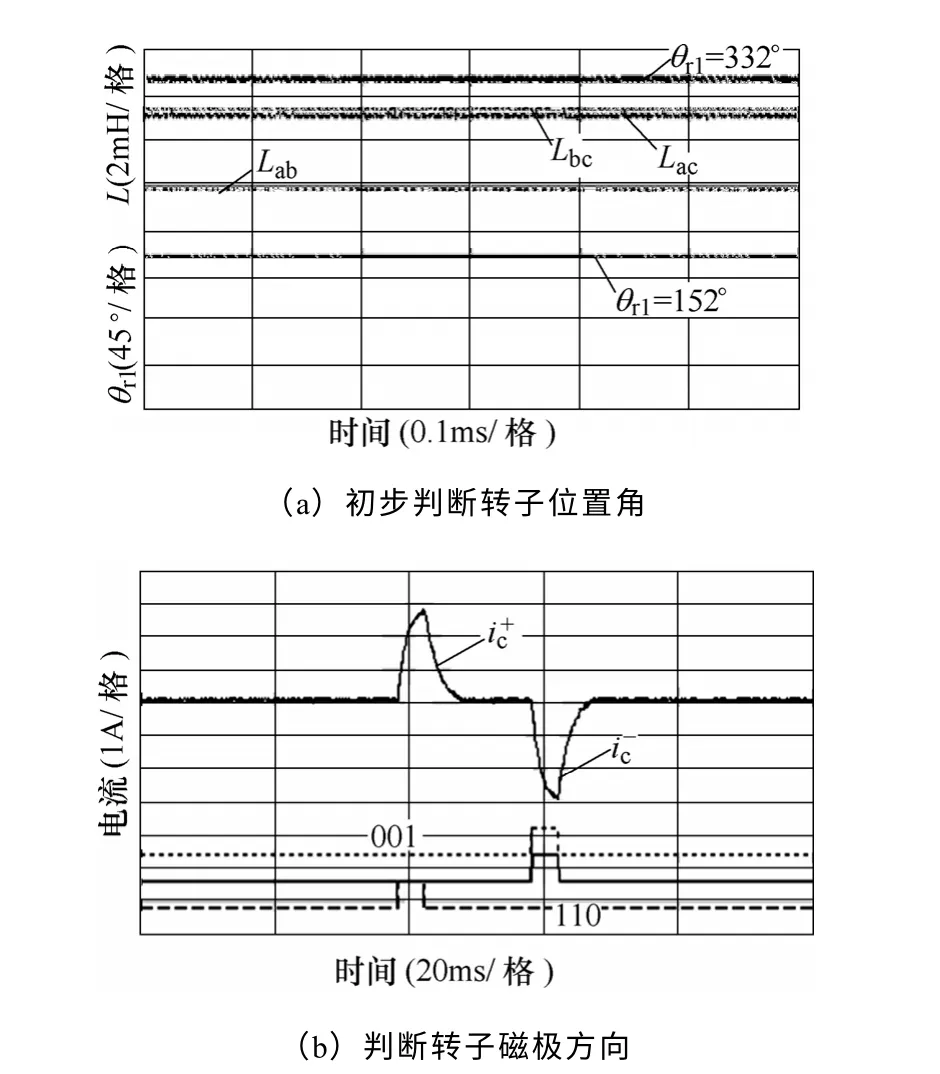
图16 转子初始位置在150°时的实验波形Fig.16 Experimental waveforms of rotor initial position on 150°

图17和图18分别为转子位置对比图和位置估计误差图，从图中可以看出，该方法可以准确的估计转子位置角，误差最大为±5°，可以满足绝大部分应用场合的准确度要求，误差产生的主要原因包括：电流采样误差、结构上的不对称和增磁和去磁对电感计算产生影响等，其中增磁和去磁现象是造成边界区域处误差较大的主要原因。

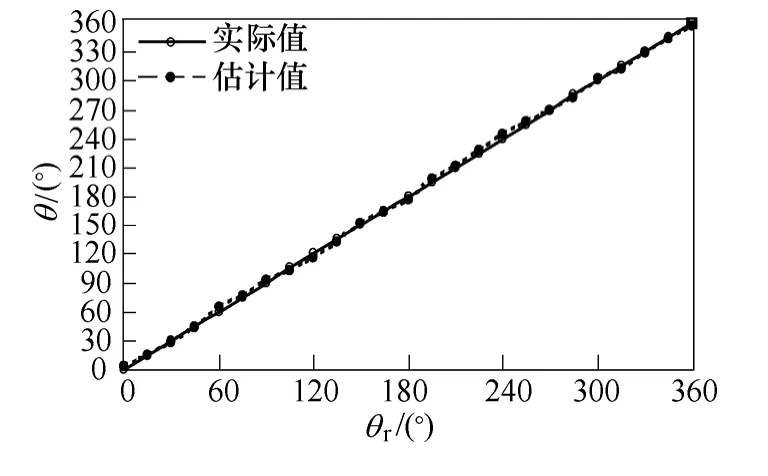
图17 转子估算位置和实际位置对比Fig.17 Comparison of estimated rotor position and real rotor position

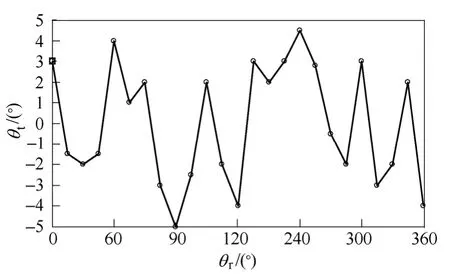
图18 转子初始位置估算误差Fig.18 Experimental of rotor initial position estimation error

3 结论

本文提出了一种转子初始位置检测的新方法，最后搭建以A&D 实时仿真装置为控制中心的实验平台，验证了所提算法的可行性和正确性，得到如下结论。

（1）从凸极效应对绕组电感的影响出发，分析了绕组自感和互感随转子位置的变化规律，推导出线电感与转子位置角的关系，提出了一种通过注入高频低压脉冲来进行线电感辨识的方法。

（2）利用傅里叶级数分解，引入线电感随绕组电流变化的基波分量和二次谐波幅值，深入分析了绕组电流对线电感的影响，同时选取最优的电压脉冲施加时间，提高了线电感辨识准确度。

（3）建立了角度-线电感关系的数学模型，利用旋转坐标变换初步计算出转子初始位置角，随后结合铁心饱和效应，改进了一种适用于磁极极性判断的方法。

[1]Dutta R,Rahman M F.Design and analysis of an interior permanent magnet(IPM)machine with very wide constant power operation range[J].IEEE Transactions on Energy Conversion,2008,23(1):25-33.

[2]Jia Hongyun,Cheng Ming,Hua Wei,et al.A new stator-flux switching permanent motor drive based on voltage space-vector[C].IEEE International Conference on Electrical Machines and System,2008:3032-3036.

[3]Li W J,Sul S K.A new starting method of BLDC motors without position sensor[J].IEEE Transactions on Industry Applications,2006,42(6):1532-1538.

[4]韦鲲,金辛海.表面式永磁同步电机初始转子位置估计技术[J].中国电机工程学报,2006,26(22):104-109.

Wei Kun,Jin Xinhai.Initial rotor position estimate technique on surface mounted permanent magnet synchronous motor[J].Proceedings of the CSEE,2006,26(22):104-109.

[5]Wang Yi,Guo Ningning,Zhu Jiangguo,et al.Initial rotor position and magnetic polarity identification of PM synchronous machine based on nonlinear machine model and finite element analysis[J].IEEE Transac- tions on Magnetics,2010,46(6):2016-2019.

[6]Nakashima S,Inagaki Y,Miki I.Sensorless initial rotor position estimation of surface permanent- magnet synchronous motor[J].IEEE Transactions on Industry Applications,2000,36(6):1598-1630.

[7]王子辉,陆凯元,叶云岳.基于改进的脉冲电压注入永磁同步电机转子初始位置检测方法[J].中国电机工程学报,2011,31(36):95-101.

Wang Zihui,Lu Kaiyuan,Ye Yunyue.Initial position estimation method for permanent magnet synchronous motor based on improved pulse voltage injection[J].Proceedings of the CSEE,2011,31(36):95-101.

[8]Gong L M,Zhu Z Q.Robust initial rotor position estimation of permanent-magnet brushless AC machines with carrier-signal-injection-based sensorless control[J].IEEE Transactions on Industry Applications,2013,49(6):2602-2609.

[9]Kim H,Hun K K,Lorenz R D,et al.A novel method for initial rotor position estimation for IPM synch- ronous machine drives[J].IEEE Transactions on Industry Applications,2004,40(5):1369-1378.

[10]陈书锦,李华德,李擎,等.永磁同步电动机起动过程控制[J].电工技术学报,2008,23(7):39-44.

Chen Shujing,Li Huade,Li Qing,et al.Start process control of permanent magnet synchronous motors[J].Transac- tions of China Electrotechnical Society,2008,23(7):39-44.

[11]王高林,杨荣峰,于泳,等.内置永磁同步电机转子初始位置估计方法[J].电机与控制学报,2010,14(6):57-60.

Wang Gaolin,Yang Rongfeng,Yu Yong,et al.Initial rotor position estimation for interior permanent magnet synchronous motor[J].Electric Machines and Control,2010,14(6):57-60.

[12]Ha J I,Ide K,Sawa T,et al.Sensorless rotor position estimation of an interior permanent-magnet motor from initial states[J].IEEE Transactions on Industry Applications,2003,39(3):761-767.

[13]贾洪平,贺益康.基于高频注入法的永磁同步电机转子初始位置检测研究[J].中国电机工程学报,2007,27(15):15-20.

Jia Hongping,He Yikang.Study on inspection of the initial rotor position of a PMSM based on high- frequency signal injection[J].Proceedings of the CSEE,2007,27(15):15-20.

[14]刘家曦,李立毅.考虑磁场交叉耦合的内嵌式永磁同步电机初始位置检测技术[J].电工技术学报,2013,28(7):32-38.

Liu Jiaxi,Li Liyi.Initial rotor position estimation considering magnetic cross coupling based on IPMSM[J].Transactions of China Electrotechnical Society,2013,28(7):32-38.

[15]万山明,吴芳,黄声华.基于高频电压信号注入的永磁同步电机转子初始位置估计[J].中国电机工程学报,2008,28(33):82-86.

Wan Shanming,Wu Fang,Huang Shenghua.Initial rotor position estimation of permanent magnet synchronous motor based on high frequency voltage signal injection method[J].Proceedings of the CSEE,2008,28(33):82-86.

[16]李毅拓,陆海峰,瞿文龙.一种新颖的永磁同步电机转子初始位置检测方法[J].中国电机工程学报,2013,33(3):75-82.

Li Yituo,Lu Haifeng,Qu Wenlong.A novel initial rotor position estimation method for permanent magnet synchronous motors[J].Proceedings of the CSEE,2013,33(3):75-82.

[17]蔡骏,邓智泉.基于电感线性区模型的开关磁阻电机无位置传感器技术[J].中国电机工程学报,2012,32(15):114-123.

Cai Jun,Deng Zhiquan.Sensorless control of switched reluctance motor based on the phase inductance model in linear regions[J].Proceedings of the CSEE,2012,32(15):114-123.

[18]Kulkarni A B,Ehsani M.A novel position sensor elimination technique for the interior permanent- magnet synchronous motor drive[J].IEEE Transactions on Industry Applications,1992,28(1):144-150.

[19]王强,王友仁,孔德明,等.隐极式无刷直流电机转子初始位置估计[J].中国电机工程学报,2012,32(33):105-110.

Wang Qiang,Wang Youren,Kong Deming,et al.Initial rotor position estimation for non-salient pole brushless DC motors[J].Proceedings of the CSEE,2012,32(33):105-110.

[20]Champa P,Somsiri P,Wipasuramonton P,et al.Initial rotor position estimation for sensorless Brushless DC drives[J].IEEE Transactions on Industry Applications,2009,45(4):1318-1324.

[21]Gambetta D,Ahfock A.New sensorless commutation technique for brushless DC motors[J].IET Electric Power Applications,2009,3(1):40-49.

[22]史婷娜,吴志勇.基于绕组电感变化特性的无刷直流电机无位置传感器控制[J].中国电机工程学报,2012,32(27):45-52.

Shi Tingna,Wu Zhiyong.Sensorless control of BLDC motors based on variation behavior of winding[J].Proceedings of the CSEE,2012,32(27):45-52.