机载天文导航系统中振动对导航精度的影响

董强，马彩文，李艳，杨晓许，袁辉

（1.中国科学院西安光学精密机械研究所，陕西西安710119；2.中国科学院大学，北京100049）

机载天文导航系统中振动对导航精度的影响

董强1，2，马彩文1，李艳1，杨晓许1，袁辉1，2

（1.中国科学院西安光学精密机械研究所，陕西西安710119；2.中国科学院大学，北京100049）

针对平台式机载天文自主导航系统载体振动对导航系统定位精度的影响问题，理论分析了载体对导航平台影响的振动形式，给出振动角位移是主要影响量的结论。研究了天文导航系统的单星定位导航建模思路，根据振动角位移的特点给出了角位移补偿中近似坐标转换矩阵。设计了振动实验，建立了定位模型，给出了载体振动主要以角位移的形式将误差传递给导航系统平台。试验结果表明：振动角位移带来的误差为天文导航定位的主要影响因素，X、Y轴200″的轴向振动角位移带给天文导航系统的定位误差近似为600 m。

天文导航；振动；角位移；单星定位

机载惯导／天文自主导航系统是利用天文导航系统的隐蔽性好、自主性强、能够提供高精度姿态信息等特点，结合高精度的惯性导航系统，实现飞机高精度、长航时所需的组合自主定位与导航系统［1］。惯性／天文导航经过50余年的发展，理论研究相对透彻，工程应用却鲜有提及。根据现阶段的研究现状，惯性导航系统主要研究点：惯性器件技术、误差补偿与抑制技术、导航算法；天文导航系统主要研究点：星敏感技术、平台测量技术、目标解算／穏像方法、导航算法；惯性和天文组合导航主要研究点：信息融合、组合模式、导航解算［2］。

以天文导航中平台测量精度的高频抑制技术作为出发点，研究了因载体振动带来的平台测量精度的下降而影响导航系统精度问题。分别讨论了载体振动影响的方式［3］、单星定位原理［4］，最后结合现有技术设计实验，测量导航研制样机的振动位移量，编写单星导航仿真程序，将振动影响作为误差进行仿真，最后给出实验和仿真结果。

1 载体振动源的误差分析

机载天文导航系统，在可观测星极少的情况下（导航星等2.5 m，最多仅50颗），将观测设备安装在动载体平台上，弥补固定点观测的不足，实现全天观测功能。但是动载体平台的引入却带来了新的问题：平台的振动将导致光学系统成像质量的下降进而导致观测性能降低，更为致命的是由于飞机的振动将带来平台的抖动，进一步影响导航系统中的坐标系标准的改变，这样的影响带给天文导航系统的误差较大，直接影响天文导航的精度，严重的振动有可能导致天文导航系统失效。所以如何有效的隔离飞机振动带来的影响，成为天文导航高精度要求下，必须解决的问题。

航空环境中振动是必然存在且无法避免的，振动严重影响各种机载设备的性能指标。飞机的振动是无法消除的，通常的机载设备都会采用各种减震措施（被动减振、主动减振）降低振动带来的影响。最直接、常用的方法是采用各种有效的减振措施衰减集体振动，进而降低振动对机载设备的影响。衰减振动前，必须清楚需要衰减的振动形式。线位移振动（平台沿坐标轴方向移动）和角位移振动（平台绕坐标轴进行旋转运动）的衰减方法不同，因此需要分析振动线位移和振动角位移对平台系统的影响［5］。

天文导航系统所观测的（目标）恒星是绝对不动的，速度为零，以光学系统的节点作为坐标原点，光学系统的光轴作为Z轴，建立三维正交坐标系，恒星导航观星光学系统的空间转台振动形式可以分解为2部分：沿X、Y、Z轴方向的线位移振动和绕X、Y、Z轴旋转的角位移振动。天文导航系统平台坐标系简图如图1所示。

图1 机载天文导航系统平台坐标系Fig.1 Airborne celestial navigation system platform co⁃ordinate system

文献［5］结合天文导航系统平台形式，平台的振动形式分别为振动线位移和振动角位移，对比分析不同轴的振动线位移和振动角位移。

X轴（Y轴情况相同）振动角位移与线位移对比：

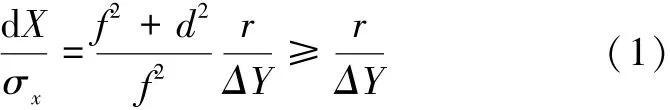
X轴（Y轴情况相同）与Z轴矢量方向上振动角位移对比：

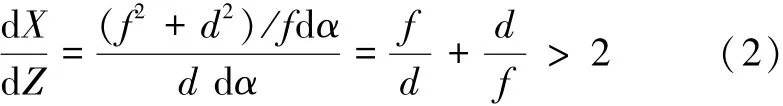
式中：r为观测点与观测恒星的垂直距离，可认为是无穷大，ΔY为Y轴上的线位移，则可得到dX／σx→∞。

结合上述理论分析，可以得出平台因为振动所产生的角位移量远远大于线位移量，X轴（Y轴）产生的角位移量是Z轴（光轴）产生的角位移量的2倍以上。

2 天文导航单星定位原理

采用单星定位原理［6］。星体S在天球中的位置如图2所示，根据星体、观测平台及部分天文信息可以得到导航三角形PZS。由天北极P、天顶Z和天体S成的球面三角形称为导航三角形。即是由测者午半圆、天体时圆和天体方位圆（通过天体、天体的天顶和天底的圆）所构成的球面三角形。

导航三角形有以下9个要素，3个顶点：天顶P、天极S、天北极Z；3个边：余纬为90°-φ、极距为90°-δ、顶距为90°-h；3个角：方位角A、时角LHA、天体的位置角q。

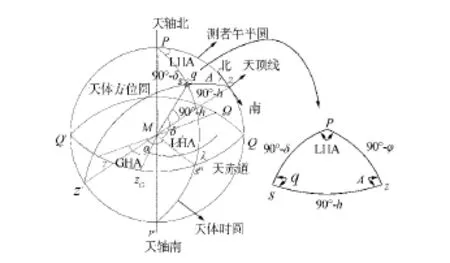
图2 导航星在天球中的位置及导航三角形Fig.2 Navigation stars on the celestial sphere positionand navigation triangle

根据球面三角形正余弦定理、天球赤道面上经度和时间关系和导航三角形，可以得出：

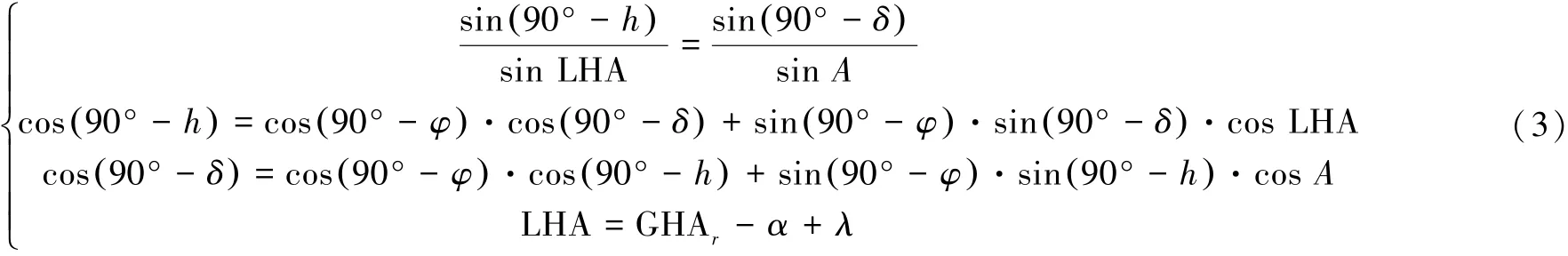
式（3）可化简为

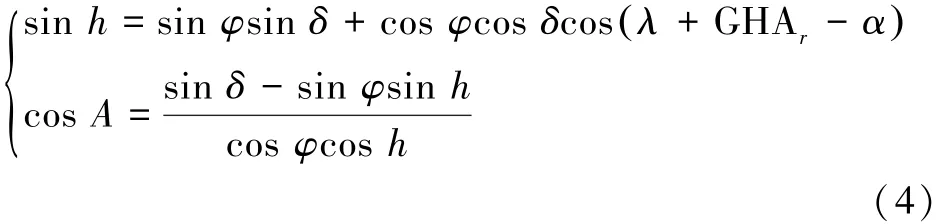
根据单星定位理论，可以总结出上述导航原理流程如图3所示。输入分为通过天文年历查到的LHA、GHAr、α、δ（天体的地方时角、春分点格林时角、天体的赤经、天体的赤纬），通过平台测量得到的h、A（高度角、方位角）。输出为λ、φ（经度、纬度），根据上述公式可以通过天文信息和测量信息求出导航信息。

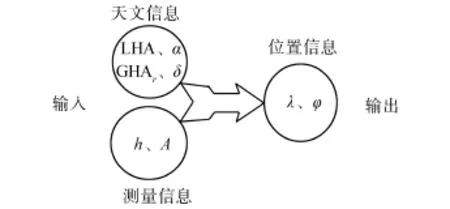
图3 导航原理简图Fig.3 The principle of navigation

3 天文导航平台的坐标系转换

理想情况下，平台坐标系与飞机固联，则平台坐标系和地理坐标系重合，但因为平台和飞机之间采用了减震系统联接，导致地理坐标系与平台坐标系产生夹角，而在导航系统中，这个夹角影响到了导航坐标系转换，进而影响着导航系统的定位精度，所以恒星导航中振动角位移误差产生的影响必须进行考虑。

图4为平台和飞机坐标系关系简图。假设坐标系XYZ是理论上平台（飞机）的坐标系，坐标系X'Y'Z'为振动后的平台坐标系。天文导航系统中，导航解算是从平台的方位角和高度角结算出飞机的经纬度信息和姿态信息。当平台与飞机产生夹角时候，解算出来的是平台的姿态信息。所以在解算的过程中，必须要考虑振动角位移产生的影响。在解算初期需要将平台的方位高角信息转换成飞机的方位和高角信息。这就需要加入坐标系转换环节。

如图4所示，假设XYZ坐标系（平台坐标系）分别绕X、Y、Z轴旋转θ、γ、ψ（单位为rad）得到X'Y'Z'（飞机坐标系）。则姿态转换矩阵如式（5）所示［7］：

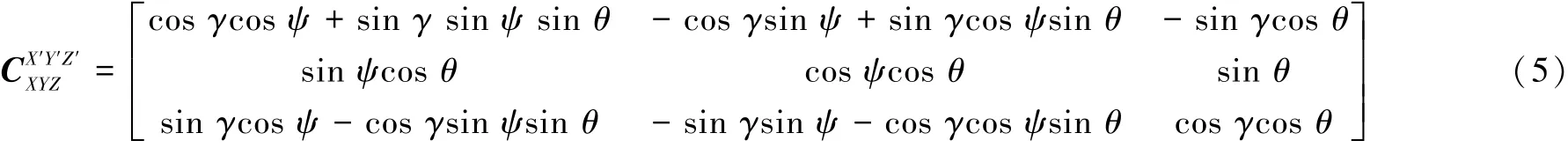
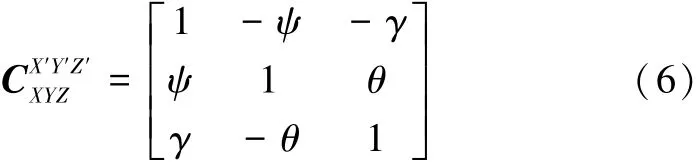
平台和飞机之间的坐标系转换属于无限转动与旋转次序无关。因振动角位移导致平台和飞机坐标系的不平行问题解决方法中，无限转动与旋转次序无关可以大大减少角位移补偿的计算量，提高计算速度。

图4 平台与机体坐标系Fig.4 The coordinate system of platform and airplane

4 实验仿真分析

本文以中科院西安光学精密机械研究所研制的机载天文自主导航原理样机作为减振器减振误差源进行测量计算。样机平台减震采用辽宁同泽的JLZ型六维等刚度减震器。此减震器的静态变位（压缩、拉伸）分别为5±1 mm、3.5±1 mm。工程中减振器安装方法如图5所示，选用所安装的减震器之间距离为300 mm。假设工作中，4个角中安装的减震器分别产生了一定变位，角位移导致的平台产生θ角度的倾斜。平台振动角位移测量原理如图6所示［8］。

图5 减震器安装简图Fig.5 Shock absorber installation diagram

图6 振动产生的角位移及测量原理Fig.6 The measurement principle of vibration angular displacement

角度θ的测量采用成都光电所生产的光自准直仪。在原理样机前侧面和右侧面分别安装反射镜，前侧和右侧摆放自准直仪。振动试验中激励测试体的振动信号是模拟飞机挂点的振动信息量。振动激励后，前侧自准直仪可以输出平台绕Y、Z轴的振动角位移，右侧自准直仪可以输出平台绕X、Z轴的振动角位移。

测试结果如表1所示。根据表1测量结果，可以解算出X、Y、Z轴的振动角位移均方值分别为：dXrms＝216.5″，dYrms＝212.8″，dZrms＝23.4″。

建立天文导航数学模型［10］，解算平台振动角位移误差对导航精度的影响。仿真天文导航中X、Y、Z轴振动角位移误差对天文导航位置精度的影响。将X、Y、Z轴的振动角位移分别作为误差量带入进行仿真。X轴误差赋予200″误差，Y、Z轴同时赋予10″误差（Y、Z轴仿真条件与X轴相同，仿真时设置仿真轴误差为200″，设置其他2轴仿真误差为10″）。X、Y、Z轴误差对天文导航精度仿真曲线如图7所示。

表1 振动角位移Table1 The measurement of vibration angular displacement

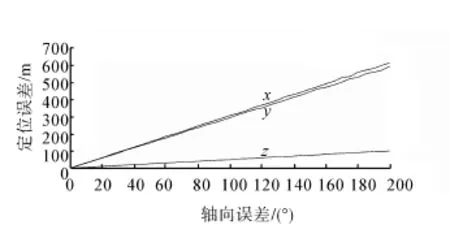
图7 振动角位移误差对导航精度的影响Fig.7 The navigation error of vibration angular displacement

仿真结果显示：

1）轴向振动角位移带入的误差和对导航系统产生的定位精度近似呈线性关系。

2）X、Y轴上200″的轴向振动角位移对天文导航将产生600 m的导航误差。

3）Z轴上200″的轴向振动角位移对天文导航将产生100 m的导航误差。

根据对样机平台的测量和天文导航数学模型仿真，可以验证理论中：

1）振动角位移是振动线位移的数倍，振动线位移可忽略不计。

2）X（Y）轴的振动角位移大于Z轴振动角位移的2倍。

3）振动角位移带来的误差对天文导航定位精度有致命的影响。

4）Z轴振动角位移对天文导航定位精度的影响小于X、Y轴振动角位移对天文导航定位精度的影响的1／6。

5 结论

针对飞机振动对机载天文导航定位问题进行分析，给出了影响原因及结果，但未对问题给出解决方法，飞机振动影响问题将在下一步工作中进行分析解决，初步提出了振动角位移补偿技术，即测量振动角位移量，将振动角位移误差带入导航解算过程进行补偿。机载惯性／天文组合导航技术国内研究已进行数年，理论研究相对透彻，但实际工程应用却鲜有所见，飞机振动对天文导航定位影响在文献中也未见提及，所以文中研究内容对后续机载惯导／天文导航系统的精度提高有一定意义，对工程项目有实际应用价值。飞机振动位移的影响对后续天文导航技术研究提供一定基础，有效解决飞机振动位移影响也是本课题进一步研究的重要内容。

［1］JAMSHAID A.In⁃flight alignment of inertial navigation sys⁃tem by celestial observation technique［J］.Journal of Nan⁃jing university of aeronautics and astronautics，2011，22（2）：236⁃239.

［2］QU Q.Airborne INS／CNS Deeply integrated Algorithm on celestial angle observation［J］.Journal of Nanjing university of aeronautics and astronautics，2011，43（6）：766⁃769.

［3］CHIAPPETTA M J.Celestial navigation systemforan［P］.US：20l00082l93Al，2010⁃04⁃01.

［4］RICHARD A.Electronic celestial navigation［P］.US：397695710，1993⁃11⁃06.

［5］梁爽.无角位移减震器的机理研究［D］.长春：长春理工大学，2011：10⁃15.

LIANG Shuang.Study on principle of rotation displacement isolator［D］.Changchun：Changchun University of Technol⁃ogy and Science，2011：10⁃15.

［6］刘真.基于天文导航的无人机定位研究［D］.西安：西安电子科技大学，2009：44⁃59.

LIU Zhen.Study on UAV positioning based on celestial navi⁃gation［D］.Xi'an：Xidian University，2009：44⁃59.

［7］秦永元.惯性导航［M］.北京：科学出版社，2006：7⁃8.

［8］QIANG D，XIAOXU Y.The co⁃simulation of airborne stable platform based on adams／simulink［C］／／Proceedings of the 27th Conference of Spacecraft TT and C Technology in Chi⁃na.Guangzhou，China，2014：49⁃57.

［9］卢温昭.单星定位时影响定位精度的研究［J］.卫星与网络，2010，91（1）：71⁃73.

LUN Wenzhao.Research on the factors that affect the accu⁃racy of positioning by single satellite［J］.Satellite and Net⁃work，2010，91（1）：71⁃73.

［10］WANG Y D，SUN J F，ZHENG W.Interstellar autonomous navigation system using X⁃ray pulsar and stellar angle measurement［J］.Applied Mechanics and Materials，2013，249（1）：231⁃240.

Influence of vibration in the airborne celestial navigation system on navigation accuracy

DONG Qiang1，2，MA Caiwen1，LI Yan1，YANG Xiaoxu1，YUAN Hui1，2
（1.Xi'an Institute of Optics and Precision Mechanics of CAS，Xi'an 710119，China；2.University of Chinese Academy of Sciences，Beijing 100049，China）

For the issue of the influence of aircraft vibration on the navigation system positioning accuracy based on airborne autonomous celestial navigation system，an analysis of navigation platform vibration influenced from aircraft was preceded.Furthermore，a conclusion was given that the main factor is vibration angular displacement.Next，a single stellar positioning model in the celestial navigation system was established.According to the characteristics of vibration angular displacement，the similar coordinate transformation matrix in the angular displacement compensa⁃tion was given.The results of vibration experiment and positioning model simulation validated that the angular vibra⁃tion is the main error propagation to navigation system platform.The positioning error of celestial navigation system is 600 m when vibration angular displacement is 200 s along the x and y axis.

celestial navigation；vibration；angular displacement；single stellar positioning

10.3969／j.issn.1006⁃7043.201404048

http：／／www.cnki.net／kcms／doi／10.3969／j.issn.1006⁃7043.201404048.html

V249.4

A

1006⁃7043（2015）02⁃0209⁃04

2014⁃04⁃14.网络出版时间：2014⁃11⁃27.

国家863计划资助项目（2013AA7031002D）.

董强（1986⁃），男，博士研究生；

马彩文（1967⁃），男，研究员，博士生导师.

董强，E⁃mail：dongqiang＠opt.cn