混行条件下直线式公交站点停靠车辆数优化

孙锋，黄玲，叶盈，王殿海

（1.浙江大学建筑工程学院，浙江杭州310058；2.科技部高技术研究发展中心，北京100862；3.山东理工大学交通学院，山东淄博255049；）

混行条件下直线式公交站点停靠车辆数优化

孙锋1，3，黄玲2，叶盈1，王殿海1

（1.浙江大学建筑工程学院，浙江杭州310058；2.科技部高技术研究发展中心，北京100862；3.山东理工大学交通学院，山东淄博255049；）

针对公交站点排队溢出导致的路段运行效率下降问题，通过分析混行交通条件下公交跳站运行对路段通行能力及乘客出行时间的影响，分别建立了小汽车和公交乘客的出行时间计算模型，并在此基础上建立了以乘客总出行时间最小为目标的公交站点停靠车辆数优化模型；以杭州市天目山路为例，使用上述方法对其站点停靠车辆数进行了优化，结果显示，优化后的停靠方案能够使小汽车运行速度提高9.32%，公交乘客的出行时间缩短3.98%，所有出行者的总出行时间减少4.75%；本文提出方法的优化结果能够为混行交通条件下公交跳站运行方案的设计提供基础。

公共交通；公交站点；跳站运行；出行时间

根据公交乘客的出行特性，设计合理的公交跳站运行方案，不但能够提高公交出行的效率，也能够减少站点停靠车辆数，缓解站点处的供需矛盾［1⁃2］。近年来，上海、深圳等城市也开始采用这一措施，但由于制定运行方案时缺少科学依据，出现了站点资源利用不充分、乘客出行不方便等问题。因此，有必要针对我国目前的交通发展状况，对公交跳站式运行下的交通运行特征进行系统性研究。

在公交运行组织研究方面，国内外已经积累了丰富的研究成果，Leiva［2］、Fu［3］、Eberlein［4］、Niu［5］等通过分析公交跳站运行对乘客出行的影响，建立了以公交乘客出行时间最小为目标的优化模型，并认为合理的跳站运行管理能够提高公交出行效率和减少公交运行成本。但是，这些研究都是针对公交系统内部进行的，并没有考虑公交车辆与社会车辆之间的相互作用，而我国目前很多城市道路上仍然采用混合通行，已有的成果难以直接应用。为此，本文在考虑公交车与社会车辆相互作用的基础上，分析混行交通条件下公交跳站运行对路网运行效率及乘客出行时间的影响，并建立以出行时间最小为目标的公交站点停靠车辆数优化模型。

1 混行交通条件下小汽车出行时间

1.1 研究对象

本文以设置直线式停靠站的城市主干路为研究对象，每个研究单元包含1条路段、1个交叉口和1个公交站点，其形式如图1所示。

图1 研究单元图Fig.1 Studied road unit

为了方便建立模型，采取以下假设：

1）路网中只有公交车和小汽车2种交通方式；

2）公交乘客均匀分布在乘车站点周围，而且到达站点的时间是随机的；

3）某条公交线路在站点i实施跳站后，受影响乘客都通过在其他站点换乘以到达目的地。

1.2 路段行驶时间理论模型

小汽车的出行时间包括2部分：路段行驶时间和交叉口延误时间，通过式（1）计算。

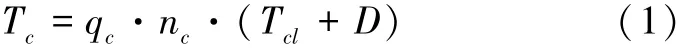
式中：Tc为单位小时内小汽车乘客在研究单元中的总行程时间，s；Tcl为小汽车在路段上的平均行驶时间，s；D为交叉口延误时间，s；qc为小汽车的交通量，pcu／h；nc为小汽车的载客人数，人／辆。

交叉口延误已有成熟的结论，而路段行驶时间主要取决于路段的通行能力和交通流量，设置公交站点路段的通行能力受到停靠车辆数的影响［6］。

1.3 路段通行能力

在公交站点影响路段，由于公交车进出站及停靠对社会车辆的通行造成影响，导致路段通行能力的下降，一般通过公交停靠站对道路通行能力的折减系数来计算［1］：

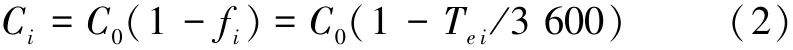
式中：Ci为单车道折减后的通行能力，pcu／h；C0为单车道设计通行能力，pcu／h；fi为公交车影响下的折减系数；Tei为停靠站i车道的影响时间，s。

当所有公交车全部进站停靠时，公交车停靠的影响时间和公交站点的泊位数、站点停靠时间有关。将公交站点看作排队服务系统，则站点内没有车辆服务的概率通过下式计算［7］：

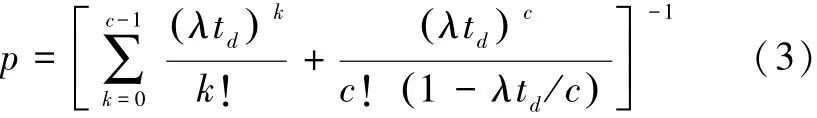
式中：p为站点内没有车辆服务的概率；c为公交站点的泊位数；td为站点停靠时间，s；λ为公交车的到达率，辆／s。

公交车停靠的影响时间为

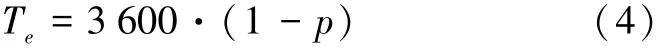
当公交站点实施跳站运行后，会出现2种情况：1）当公交车到达时，站点内没有正在接受服务的车辆，跳站车辆直接通过；2）当公交车到达时，站点有公交车正在服务，则跳站公交车只能换至内侧车道通行，对相邻车道行驶的社会车辆产生影响，根据HCM2000中结论，每发生1次公交换道行为对相邻车道的影响时间是4 s［1］。

上述第1种情况发生的概率通过下式计算［7］：

式中：p1为站点内没有车辆服务的概率λ1为停靠公交车的到达率，辆／s。

跳站运行下单位小时内对路段的总影响时间通过下式计算：

式中：ns为单位小时内实施跳站运行的公交车辆数，辆／h。

因此，该路段的通行能力通过下式计算：

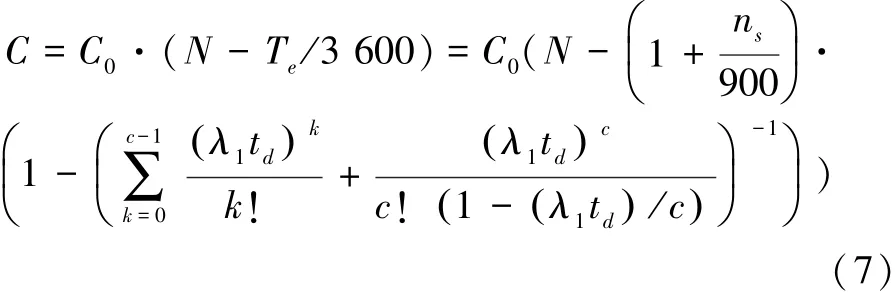
式中：C为路段通行能力；C1为最外侧车道折减后的通行能力；C2为次外侧车道折减后的通行能力；N为研究路段单向车道数，N≥2。

1.4 仿真模型建立及检验

根据实测数据在VISSIM中建立仿真路网，实测速度和仿真速度进行对比如表1，对2组数据进行t检验，得到t值为：0.761 9，小于置信度为0.05的临界值1.648。由此可知，在95%置信水平下，仿真路网模型的输出数据能够反映实际路网的运行状况，可作为交通流运行特性研究的试验环境。

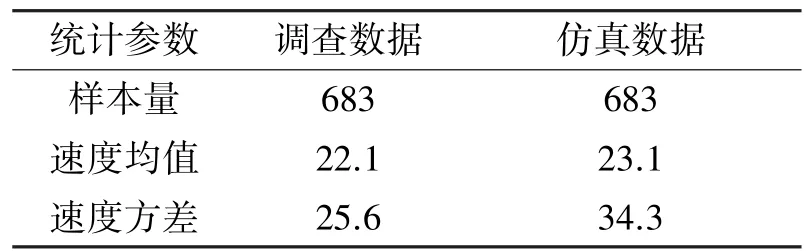
表1 现状的仿真结果与实际数据对比Table1 Comparison of the investigated values and simulation results

1.5 路段行驶时间模型标定

路阻函数的形式如（8）所示［8］，可以看出，其中的参数α和β需要通过仿真数据标定。

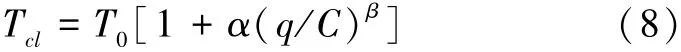
式中：T0为零流量时车辆在路段上的行驶时间，可用道路设计速度下的行驶时间代替；C为路段的可能通行能力；α、β为模型参数。

为了避免随机因素的干扰，随机数种子变化范围为41～45，每组流量仿真5次，将5次仿真数据的平均值作为最终结果。在路网模型中选择长度为340 m的路段，统计车辆在该路段上的通行时间。

本文使用最小二乘法对路阻函数中的参数进行标定，首先将式（9）变形为线性函数：

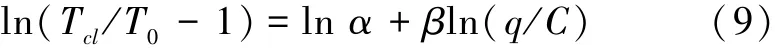
令X＝ln（q／C），Y＝ln（Tcl／T0-1），A＝β，B＝lnα，则式（9）变为

使用仿真数据标定α和β的值分别为4.2和0.87，仿真数据及拟合函数曲线如图2所示。因此，设有直线式公交停靠站的混行道路上，小汽车的路段行驶时间通过下式计算：式（11）中的C通过式（7）计算得到。

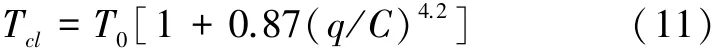
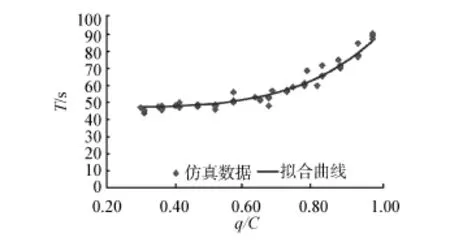
图2 小汽车路段行驶时间和（q／C）关系图Fig.2 Relationship between the travel time of car and q／C on the segment

1.6 交叉口延误

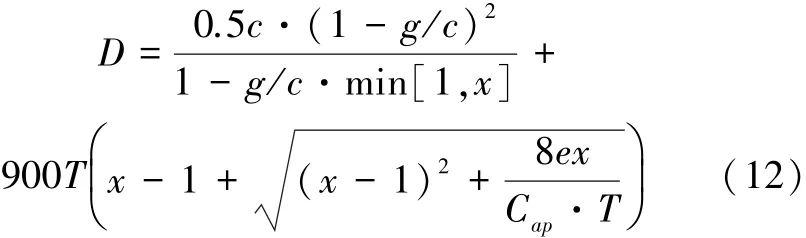
交叉口延误通过下面公式计算［1］：式中：c为交叉口周期时长，s；g为绿灯时长，s；x为计算车道的饱和度；e为交叉口信号控制类型校正系数；Cap为进口车道的通行能力，辆／h；T为分析时段的持续时长，取0.25 h。

将式（7）、（11）、（12）代入式（1）得到小汽车出行者在研究单元内的总出行时间为：

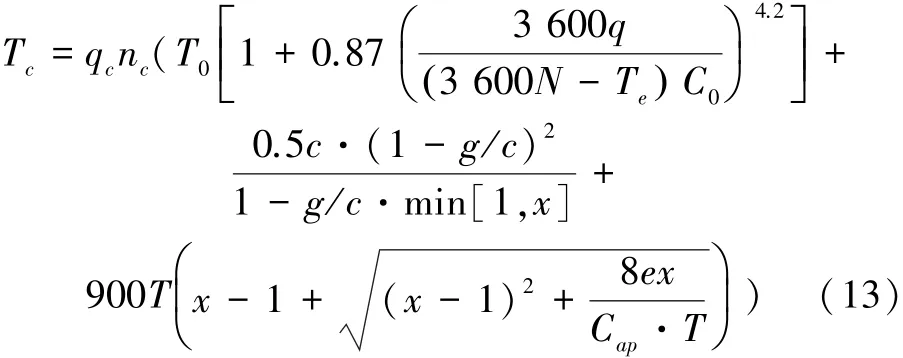
2 公交乘客出行时间计算模型

根据出行目的地不同，将公交乘客分为3类：i站上车乘客、i站下车乘客、目的地不是i站的车上乘客。在研究单元内，这3类公交乘客消耗的时间不同，受跳站运行的影响也各不相同，需要分别分析和计算［8］。

2.1 非跳站运行下乘客出行时间

在非跳站式运行下，上车乘客的出行时间包括：到站时间、等待时间和乘车时间；下车乘客的出行时间包括：离站时间和乘车时间；目的地不是i站的车上乘客的出行时间只包括乘车时间。因此，在研究单元内公交乘客的总出行时间为

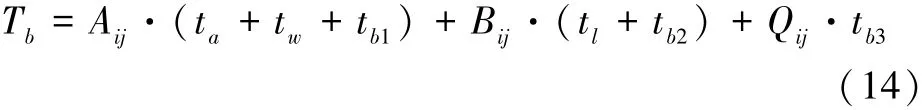
式中：Tb为非跳站运行下的公交总出行时间，s；ta为乘客到达站点的时间，s；tw为乘客在公交站点的等待时间，s；tb1为上车乘客的乘车时间，s；tl为乘客的离站到达目的地的时间，s；tb2为下车乘客的乘车时间，s；tb3为目的地不是i站的车上乘客的乘车时间，s；Aij为公交线路j在站点i的上车乘客数；Bij为公交线路j在站点i的下车乘客数；Qij为公交线路j在该路段的载客数。

1）到站或离站时间。

乘客达到站点和从站点到达目的地的平均距离都为站点间距的1／4，则到站和从站点到达目的地的平均时间表示为

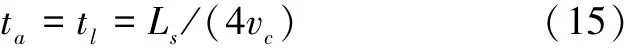
式中：Ls为公交站点的间距，m；vc为乘客到达站点的速度，步行取1.2 m／s，骑自行车取15 km／h［7］。

2）等待时间或换乘时间。

根据前面假设，乘客的等待时间和换乘时间都是随机的，仅与公交线路的发车间隔有关，其数学期望都是所乘线路发车间隔的平均值为式中：hj、hk为公交线路j和k的发车间隔，s。

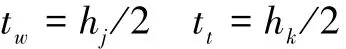
3）乘车时间。

在研究单元内，公交乘客的乘车时间主要包含：路段行驶时间、站点停靠时间和交叉口延误时间。对不同类型乘客的乘车时间分别计算如下：

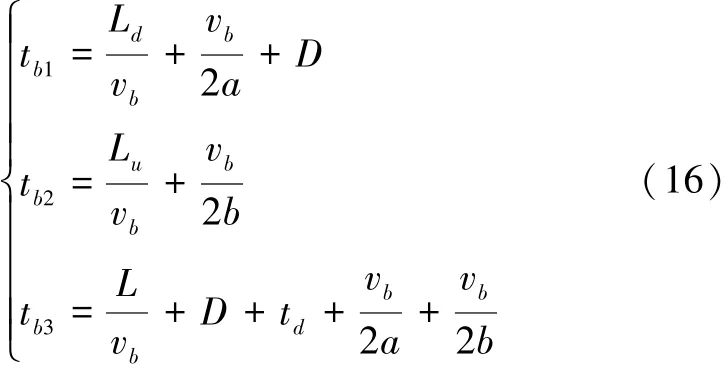
式中：Ld为站点到达下游交叉口的距离，m；Lu为上游交叉口到达站点的距离，m；L为路段长度，m；vb为公交行驶速度，m／s；b为进站的减速度，m／s2；a为出站的加速度，m／s2。

由此得到，非跳站运行下公交线路j上所有乘客的总出行时间为

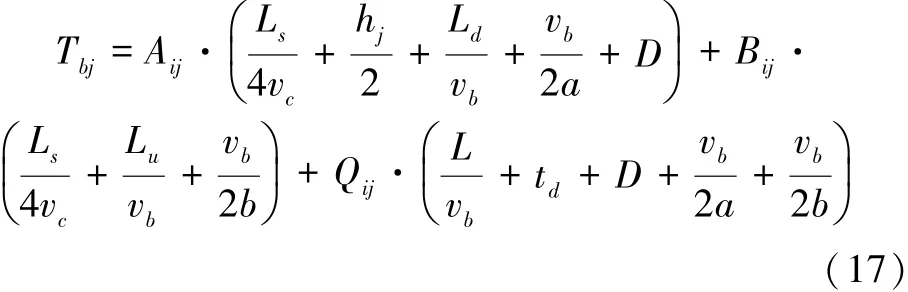
2.2 跳站运行下乘客出行时间

当公交线路j跳过站点i时，线路j的上车乘客和下车乘客的出行时间中增加了换乘时间，而车上乘客的出行时间中减少了进出站服务时间，因此，公交线路j上所有乘客的总出行时间为

3 公交站点停靠车辆数优化模型

3.1 目标函数

在公交系统的规划和运行方法设计中，一般使用出行时间对方案进行评价和优选［9］，为此，本文选择公交和小汽车出行者的总出行时间最小为优化目标，构建其目标函数为

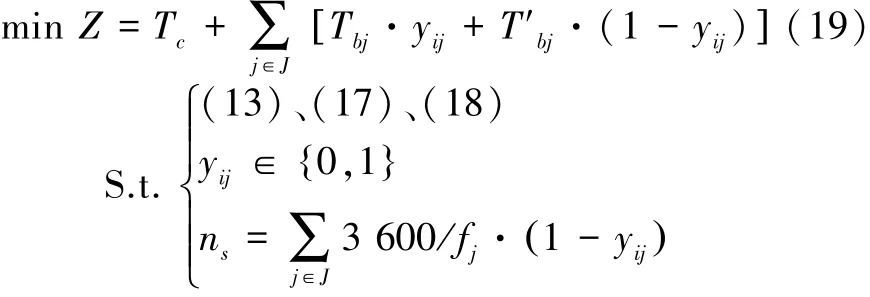
式中：J为公交站点i的所有线路的集合；yij为公交线路j在站点i的停靠属性，停靠时取1，跳过时取0，fj为线路j在站点i跳站间隔。

3.2 求解流程

上述优化模型是非线性0-1规划问题，本文选择遗传算法对模型进行求解，求解流程如图3所示［10］。

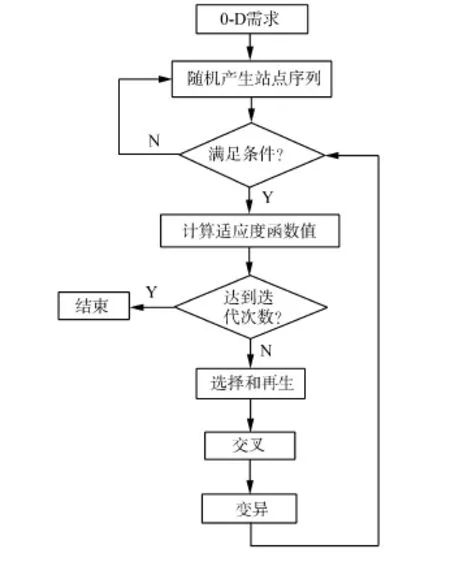
图3 最优方案的求解流程Fig.3 Overall procedure for finding an optimal scenario

4 实例验证

本文以杭州市天目山路公交流量大且交通拥堵较为严重的路段（万塘路-中山北路）为例，对公交站点停靠车辆数进行优化设计。

4.1 交通调查

通过对早高峰时段进行调查，获得了公交班次、小汽车流量、站点上下客人数等数据，如表2所示。根据调查，社会车辆载客数为2.2人／车，其他参数取值为：a＝b＝1 m／s2，vb＝30 km／h，L＝500 m。

4.2 站点停靠方案优化及结果分析

设置遗传算法的每一代种群个数为50，交叉概率为0.5，变异概率为0.01，最大迭代次数为200。将模型使用Matlab软件编制程序，然后将以上数据代入，输出小汽车和公交车的出行时间，并得到最优的公交站点停靠方案，进而得到每个站点的小时最佳停靠车辆数，如表2所示。

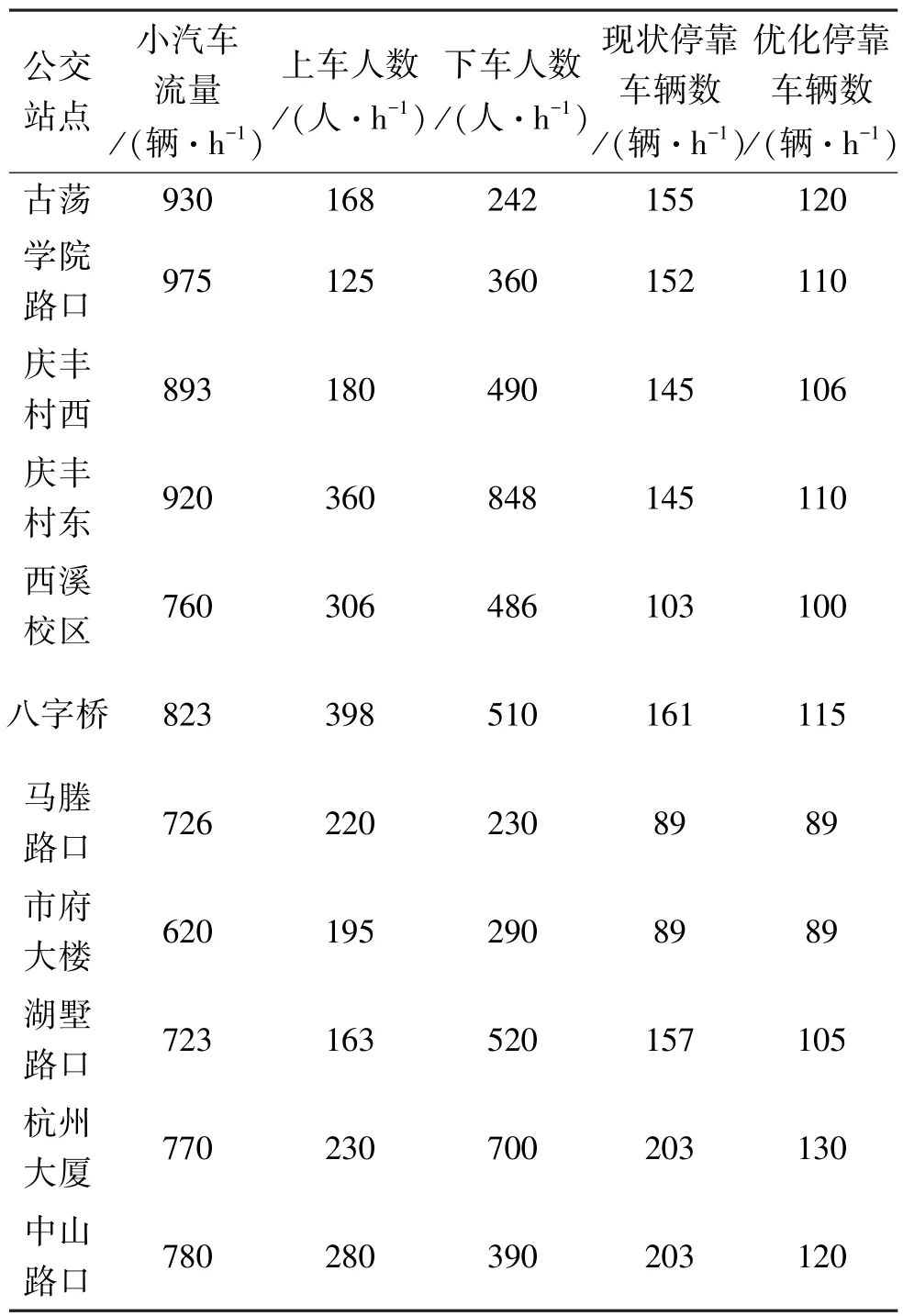
表2 公交站点调查数据及停靠车辆数优化结果Table2 Survey data and optimizing values at bus stops

在上述优化方案下，研究区域内各种方式出行时间如表3所示，可以看出，站点停靠车辆数优化后，小汽车和公交方式的总出行时间分别减少9.32%和3.98%，充分证明在不进行任何设施改造和投资条件下，通过固定式公交跳站运行能够缓解公交站点的拥堵现象，提高路网的整体运行效率。

表3 跳站运行前后的运行状态对比Table3 Comparison of traffic operation with all⁃stop and limited⁃stop operation

5 结束语

本文在分析公交跳站运行对路段通行能力及公交乘客出行时间影响的基础上，建立了公交站点停靠车辆数优化模型，并对实际路段的站点停靠方案进行优化。通过对优化前后路段运行及出行时间的分析得出，合理组织公交站点停靠车辆数可以有效减少站点路段的车流交织，从而提高道路设施利用率和居民出行效率。

［1］Transportation Research Board.Highway capacity manual 2000［M］.Washington D C：National Research Council，2000：2713⁃2715.

［2］LEIVA C，MUNOZ J C，GIESEN R，et al.Design of limit⁃ed⁃stop services for an urban bus corridor with capacity con⁃straints［J］.Transportation Research Part B，2010，44（10）：1186⁃1201.

［3］FU Liping，LIU Qing，CALAMA P I.Real⁃time optimization model for dynamic scheduling of transit operations［J］.Transportation Research Record，2003，1857：48⁃55.

［4］EBERLEIN X J.Real⁃time control strategies in transit opera⁃tions：models and analysis［D］.Cambridge，Massachusetts Institute of Technology，1995：78⁃85.

［5］NIU Huimin.Determination of the skip⁃stop scheduling for a congested transit line by bi⁃level genetic algorithm［J］.In⁃ternational Journal of Computational Intelligence Systems，2011，6（4）：1158⁃1167.

［6］杨晓光，徐辉，王健，等.港湾式公交停靠站设置条件研究［J］.中国公路学报，2011，24（1）：96⁃102.

YANG Xiaoguang，XU Hui，WANG Jian，et al.Study of setting conditions of bus bay stop［J］.China Journal of Highway and Transport，2011，24（1）：96⁃102.

［7］王炜.道路交通工程系统分析方法［M］.北京：人民交通出版社，2003：180⁃195.

［8］GARTNER N H，MESSER C J，RATHI A K.Monograph on traffic flow theory［M］.Washington DC：The Federal High⁃way Administration（FHWA），1996：112⁃118.

［9］ALONSO B，MOURA J L，IBEAS A，et al.Public transport line assignment model to dualberth bus stops［J］.Journal of Transportation Engineering，2011，137（12）：953⁃961.

［10］祁宏生，王殿海，宋现敏.路网交通状态平衡控制方法［J］.吉林大学学报：工学版，2012，42（5）：1185⁃1190.

QI Hongsheng，WANG Dianhai，SONG Xianmin.Balanced control method for road network traffic state［J］.Journal of Jilin University：EngineeringandTechnologyEdition，2012，42（5）：1185⁃1190.

Optimizing the number of buses stopping at on⁃line stops under mixed traffic conditions

SUN Feng1，3，HUANG Ling2，YE Ying1，WANG Dianhai1
（1.College of Civil Engineering and Architecture，Zhejiang University，Hangzhou 310058，China；2.High Technology Research and Development Center，The Ministry of Science and Technology，Beijing 100081，China；3.College of Transportation，Shandong Univer⁃sity of Technology，Zibo 255049，China）

Aiming at the efficiency reduction problem resulting from overloading of bus stops，the travel capacity and traffic time of passengers impacted by limited⁃stop operation are analyzed under mixed traffic condition.On this basis，the methods for computing passengers'travel time by bus and car are developed，respectively.The model of optimizing the number of buses stopping at stops with limited⁃stop operation is developed with the objective of mini⁃mizing the total travel time of the entire passengers.For this research，the Tian⁃mu⁃shan Road of Hangzhou city is used as an example.An optimal scenario is obtained with this model.The result showed that the travel speed of car after optimization increases by 9.32%，bus passengers'travel time decreases by 3.98%.The passengers'total travel time with limited⁃stop operation decreases by 4.75%shorter than that with original all⁃stop operation.In addition，the results of the proposed model can provide a basis for the design of limited⁃stop operation scenarios under mixed traffic conditions.

public transportation；bus stop；limited⁃stop service；travel time

10.3969／j.issn.1006⁃7043.201306017

http：／／www.cnki.net／kcms／doi／10.3969／j.issn.1006⁃7043.201306017.html

U491.51

A

1006⁃7043（2015）02⁃0152⁃05

2013⁃06⁃03.网络出版时间：2014⁃11⁃27.

国家973计划资助项目（2012CB725402）.

孙锋（1979⁃），男，讲师，博士；

王殿海（1962⁃），男，教授，博士.

王殿海，E⁃mail：wangdianhai＠zju.edu.cn.