两类冠图的Laplacian谱

卢鹏丽，苗玉芳

（兰州理工大学计算机与通信学院，甘肃兰州，730050）

两类冠图的Laplacian谱

卢鹏丽，苗玉芳

（兰州理工大学计算机与通信学院，甘肃兰州，730050）

图的谱蕴含着图的许多信息。冠图是一种比较复杂的图，冠图的谱更加难以计算。文中定义了两类冠图，分别是：图G1和G2的剖分图的冠点图G1◇G2和剖分图的冠边图G1☆G2。应用分块矩阵、矩阵的coronal、克罗内克积证明了两类冠图的Laplacian谱可以表示为原图G1和G2的Laplacian谱；并给出了两类冠图的生成树数目以及Kirchhoff指数。

冠图；Laplacian矩阵；Laplacian特征多项式；L-谱；生成树数目；Kirchhoff指数

冠图（corona）最早由R.FRUCHT和F.HARARY提出［1］，是为了解决如下问题：构造一些图，这些图的自同构群可由2个图的自同构群的圈积（wreath product）得到。给定2个顶点不相交的图G1和G2，将图G1的每一个顶点对应一个图G2，分别连结G1的每个顶点和其对应的G2中所有顶点所得到的图称为G1和G2的冠图。冠图的谱计算与带宽（bandwidth）［2］，最小和（minimum sum）［3］，Ramsey理论的应用［4］、可逆图、生成树数目、Kirchhoff指数等密切相关。

Kirchhoff指数和维纳指数一样，都可以用来描述化学中的分子结构［5⁃9］。然而却很难用算法［10⁃14］实现Kirchhoff指数的计算，因此给出某类图的Kirchhoff指数的界值或给出其公式表示有着重要意义。文献［15⁃20］给出了一些冠图的谱，文献［21］给出了冠图的Kirchhoff指数。

文中定义了两类冠图的变体：剖分图的冠点图G1◇G2和剖分图的冠边图G1☆G2；证明了两类冠图的Laplacian谱可以表示为原图的Laplacian谱；并给出了两类冠图的生成树数目以及Kirchhoff指数。

1 主要引理

在计算Laplacian谱时用到了矩阵的coronal和克罗内克积。

引理1［16⁃17］矩阵Mn×n的M⁃coronal记为ΓM（x），它的值为矩阵（xIn-M）-1所有元素的和，即

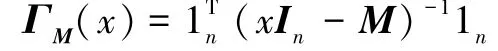
其中，1n为n维元素均为1的列向量。

引理2［17］如果矩阵Mn×n每行元素的和为一个常数t，那么就有

引理3［21］矩阵A＝（aij）m×n和B＝（bij）p×q的克罗内克积A⊗B是由aijB代替矩阵A中的元素aij得到的mp×nq维的矩阵，即

克罗内克积的相关性质有

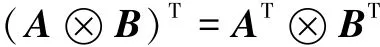
2）当矩阵AC和BD都存在时有

3）对可逆矩阵A和B有

4）对于矩阵An×n和Bp×p有

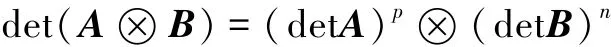
引理4［22］令t（G）代表图G生成树的个数。如果G是有n个顶点的连通图，并且它的Laplacian谱表示为0＝μ1（G）＜μ2（G）≤…≤μn（G），那么有

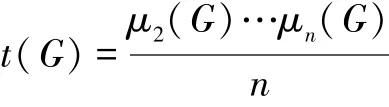
图G的Kirchhoff指数记为Kf（G），被定义为图G中所有点对之间的阻力距离之和［5，12］。

引理5［14，23］有n个顶点的连通图G的Kirchhoff指数的表达式为

式中：μ2（G），…，μn（G）是图G的非零Laplacian特征值。

2 剖分图的冠点图的谱

下面给出剖分图的冠点图的定义。剖分图的冠点图是指：给定2个顶点不相交的图G1和G2，将图G1的每一个顶点对应图G2的一个剖分图的拷贝，分别连结G1的每个顶点和其对应的G2的剖分图中所有原G2的顶点，所得到的图记为G1◇G2。

假设图G1是有n1个顶点m1条边的任意图，G2是有n2个顶点m2条边的任意图，那么G1◇G2有n1（1+ n2+m2）个顶点，m1+n1n2+2n1m2条边。

图G的剖分图S（G）是通过在G的每条边插入一个新的顶点得到的。为了将矩阵分块表示，下面给出剖分图的冠点图的顶点编号。设图G和图H都是简单有限图，分别有n1和n2个顶点，剖分图的冠点图由一个G和n1个S（H）组成。图G的顶点编号为{v1，v2，…，vn1}，n1个S（H）中原图H中的顶点记为H1，H2，…，Hn1，而n1个剖分图S（H）中新插入的顶点集记为E（H1），E（H2），…，E（Hn1）。假设H1的顶点编号为{h1，h2，…，hn2}，那么Hi的第k个顶点hk的编号为n1k+i。若E（H1）的顶点编号为{e1，e2，…，em2}，那么E（Hi）的第k个顶点的编号为（n2+k）n1+i。图1给出剖分图的冠点图的示例图。

下面给出G1◇G2的顶点度：

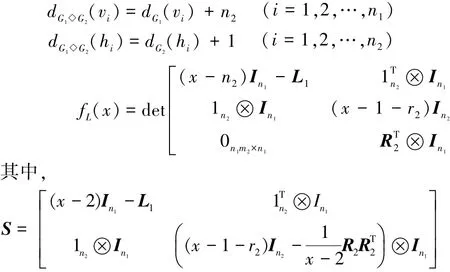
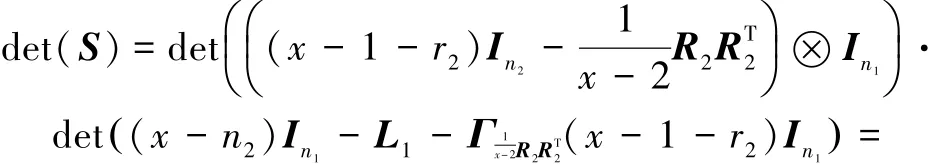
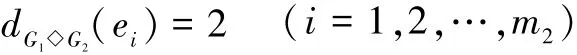
图1 剖分图的冠点图Fig.1 Corona⁃vertex of the subdivision graph

定理1 设G1是有n1个顶点的任意图，G2是有n2个顶点m2条边的r2正则图，对剖分图的冠点图有

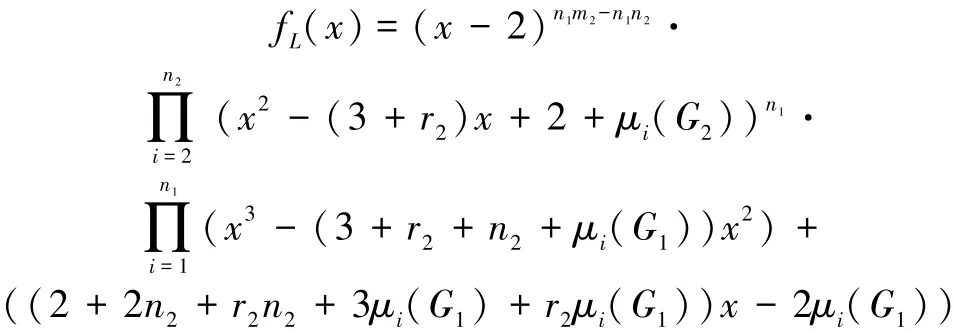
证明 设L1表示G1的Laplacian矩阵，R2表示G2的关联矩阵；由G2是r2正则图，得图G2的度矩阵为D2；那么G1◇G2的Laplacian矩阵L为

由此可得G1◇G2的Laplacian特征多项式

因此，得证。

推论1 设G1是有n1个顶点的任意图，G2是有n2个顶点m2条边的r2正则图，剖分图的冠点图G1◇G2的L⁃谱为：1）根为2，重数为n1m2-n1n2；2）对每个μi（G2），（i＝2，3，…，n2），方程x2-（3+r2）x+2+ μi（G2）＝0的2个根，每个根的重数为n1；3）对每个μi（G1）（i＝1，2，…，n1），方程（x3-（3+r2+n2+ μi（G1））x2+（2+2n2+r2n2+3μi（G1）+r2μi（G1））x-2μi（G1））的3个根。

定理2 设G1是有n1个顶点的任意图，G2是有n2个顶点m2条边的r2正则图，得G1◇G2的生成树个数为

定理3 设G1是有n1个顶点的任意图，G2是有n2个顶点m2条边的r2正则图，有Kirchhoff指数：

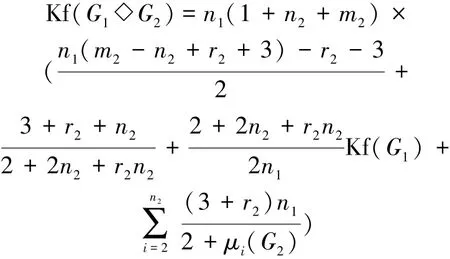
3 剖分图的冠边图的谱

下面给出剖分图的冠边图的定义。剖分图的冠边图是指：给定2个顶点不相交的图G1和G2，将图G1的每一个顶点对应图G2的一个剖分图，分别连结G1的每个顶点和其对应的G2的剖分图中所有新插入的顶点，所得到的图记为G1☆G2。

假设图G1是有n1个顶点m1条边的任意图，G2是有n2个顶点m2条边的任意图，那么G1☆G2有n1（1+n2+m2）个顶点m1+3n1m2条边。G1☆G2和G1◇G2有相同的顶点编号，图2为剖分图的冠边图的示例图。

下面给出G1☆G2的顶点度：

图2 剖分图的冠边图Fig.2 Corona⁃edge of the subdivision graph

定理4 设G1是有n1个顶点的任意图，G2是有n2个顶点m2条边的r2正则图，对剖分图的冠边图有

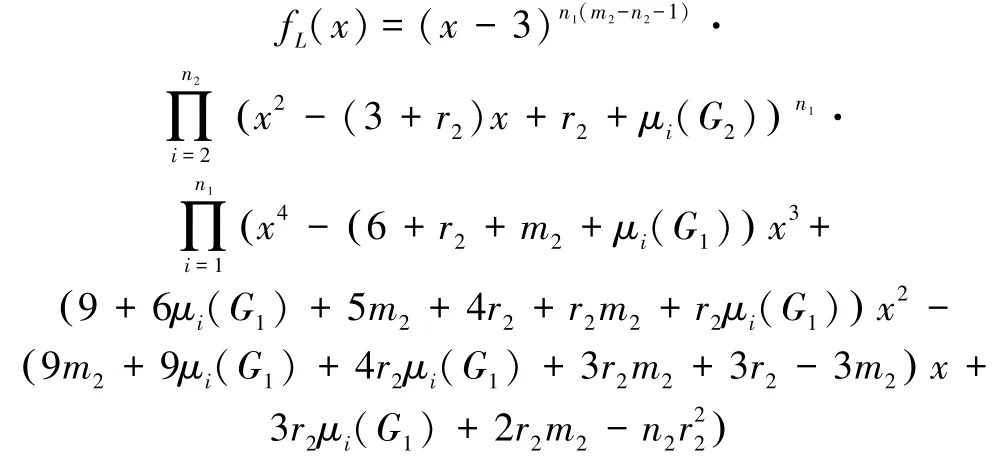
证明 设L1表示G1的Laplacian矩阵，R2表示G2的关联矩阵；由G2是r2正则图，得G2的度矩阵D2＝那么G1☆G2的Laplacian矩阵L为

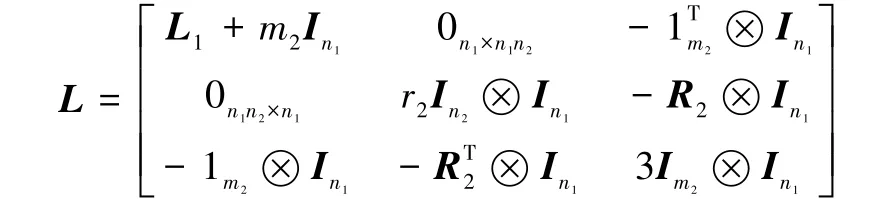
由此可得G1☆G2的Laplacian特征多项式

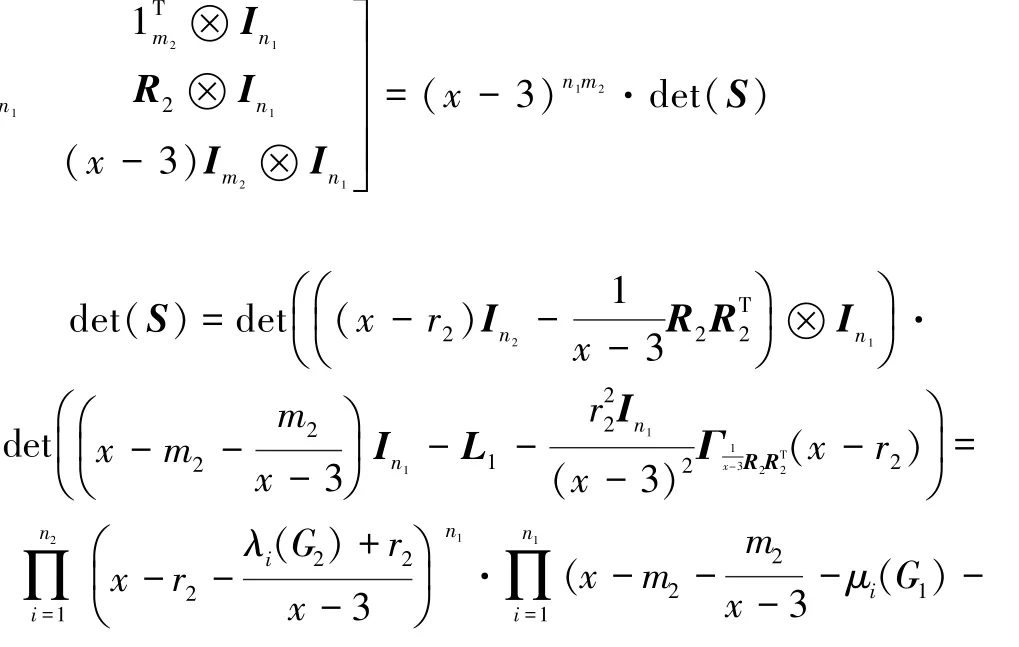
因此，得证。

推论2 设G1是有n1个顶点的任意图，G2是有n2个顶点m2条边的r2正则图，得剖分图的冠边图G1☆G2的L⁃谱为：1）根为3，重数为n1（m2-n2-1）；2）对每个μi（G2）（i＝2，…，n2），有方程x2-（3+r2）x+2+ μi（G2）＝0的2个根，每个根的重数为n1；3）对每个μi（G1）（i＝1，2，…，n1），有方程x4-（6+r2+m2+ μi（G1））x3+（9+6μi（G1）+5m2+4r2+ r2m2+r2μi（G1））x2-（9m2+9μi（G1）+4r2μi（G1）+ 3r2m2+3r2-3m2）x+2r2m2-n2r22＝0的4个根。

定理5 设G1是有n1个顶点的任意图，G2是有n2个顶点m2条边的r2正则图，有

定理6 设G1是有n1个顶点的任意图，G2是有n2个顶点m2条边的r2正则图，有Kirchhoff指数：

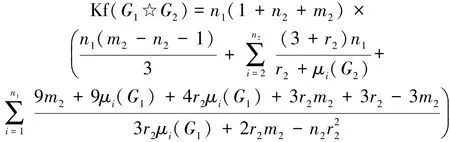
4 结论

文中定义了两类新的冠图，剖分图的冠点图G1◇G2和剖分图的冠边图G1☆G2。计算了当G1为任意图，G2为正则图时两类冠图的Laplacian谱；证明了两类冠图的生成树数目及Kirchhoff指数可以由原图的Laplacian谱表示。

［1］FRUCHT R，HARARY F.On the corona of two graphs［J］.Aequationes Mathematicae，1970，4（3）：322⁃325.

［2］CHINN P Z，YUAN J.The bandwidth of the corona of two graphs［J］.Congressus Numerantium，1992：141⁃141.

［3］WILLIAMS K.On the minimum sum of the corona of two graphs［J］.Congressus Numerantium，1993：43⁃43.

［4］NENOV N.Application of the corona⁃product of two graphs in Ramsey theory［J］.Annuaire Univ Sofia Fac Math Inform，1985，79（1）：349⁃355.

［5］BONCHEV D，BALABAN A T，LIU X，et al.Molecular cy⁃ clicity and centricity of polycyclic graphs.I.Cyclicity based on resistance distances or reciprocal distances［J］.Interna⁃tional Journal of Quantum Chemistry，1994，50（1）：1⁃20.

［6］DAS K C，GUNGOR A D，CEVIK A S.On Kirchhoff index and resistance⁃distance energy of a graph［J］.Match⁃Com⁃munications inMathematicalandComputerChemistry，2012，67（2）：541.

［7］ESTRADA E，HATANO N.Topological atomic displace⁃ments，Kirchhoff and Wiener indices of molecules［J］.Chemical Physics Letters，2010，486（4）：166⁃170.

［8］XIAO W J，GUTMAN I.Resistance distance and Laplacian spectrum［J］.Theoretical Chemistry Accounts，2003，110（4）：284⁃289.

［9］ZHOU B，TRINAJSTIC N.A note on Kirchhoff index［J］.Chemical Physics Letters，2008，455（1）：120⁃123.

［10］BABIC D，KLEIN D J，LUKOVITS I，et al.Resistance distance matrix：a computational algorithm and its applica⁃tion［J］.International Journal of Quantum Chemistry，2002，90（1）：166⁃176.

［11］BAPAT R B，GUTMAN I，XIAO W J.A simple method for computing resistance distance［J］.Zeitschrift fur Naturfors⁃chung A，2003，58（9／10）：494⁃498.

［12］KLEIN D J，RANDIC M.Resistance distance［J］.Journal of Mathematical Chemistry，1993，12（1）：81⁃95.

［13］PALACIOS J L.Resistance distance in graphs and random walks［J］.International Journal of Quantum Chemistry，2001，81（1）：29⁃33.

［14］ZHU H Y，KLEIN D J，LUKOVITS I.Extensions of the Wiener number［J］.Journal of Chemical Information and Computer Sciences，1996，36（3）：420⁃428.

［15］BARIK S，PATI S，SARMA B K.The spectrum of the co⁃rona of two graphs［J］.SIAM Journal on Discrete Mathe⁃matics，2007，21（1）：47⁃56.

［16］MCLEMAN C，MCNICHOLAS E.Spectra of coronae［J］.Linear Algebra and its Applications，2011，435（5）：998⁃1007.

［17］CUI S Y，TIAN G X.The spectrum and the signless Lapla⁃cian spectrum of coronae［J］.Linear Algebra and its Appli⁃cations，2012，437（7）：1692⁃1703.

［18］HOU Y P，SHIU W C.The spectrum of the edge corona of two graphs［J］.Electron J Linear Algebra，2010，20（58）：6⁃594.

［19］WANG S L，ZHOU B.The signless Laplacian spectra of the corona and edge corona of two graphs［J］.Linear and Mul⁃tilinear Algebra，2013，61（2）：197⁃204.

［20］LIU X G，LU P L.Spectra of subdivision⁃vertex and subdi⁃vision⁃edge neighbourhood coronae［J］.Linear Algebra and its Applications，2013，438（8）：3547⁃3559.

［21］JOHNSON C R，HORN R A.Topics in matrix analysis［M］.Cambridge：Cambridge University，1991：411⁃426.

［22］CVETKOVIC D M，DOOB M，SACHS H.Spectra of graphs：theory and application［M］.New York：Academic Press，1980：375⁃386.

［23］GUTMAN I，MOHAR B.The Quasi⁃Wiener and the Kirch⁃hoff indices coincide［J］.Journal of Chemical Information and Computer Sciences，1996，36（5）：982⁃985.

［24］ZHANG F Z.The Schur complement and its applications［M］.［S.l.］：Springer，2006：120.

Laplacian spectrum of two classes of corona graphs

LU Pengli，MIAO Yufang
（School of Computer and Communication，Lanzhou University of Technology，Lanzhou 730050，China）

The spectra contain a lot of information concerning a graph.The corona graphs are complex and the com⁃putation of their spectra is more complex.In this paper，two classes of corona graphs were defined：the corona⁃ver⁃tex of the subdivisional graph of G1and G2，denoted by G1◇G2，and the corona⁃edge of the subdivisional graph of G1and G2，denoted by G1☆G2.Using the block matrix，the coronal and Kronecker product，the Laplacian spectra of G1◇G2and G1☆G2were determined in terms of the corresponding spectra of G1and G2.By using the Laplacian spectra，the number of spanning trees and Kirchhoff index of G1◇G2and G1☆G2are also obtained.

corona graph；Laplacian matrix；Laplacian characteristic polynomial；L⁃spectrum；spanning trees；Kirchhoff index

10.3969／j.issn.1006⁃7043.201308055

http：／／www.cnki.net／kcms／doi／10.3969／j.issn.1006⁃7043.201308055.html

O157.5，O157.6

A

1006⁃7043（2015）02⁃0196⁃04

2013⁃08⁃28.网络出版时间：2014⁃11⁃27.基金项目：国家自然科学基金资助项目（11361033）.

卢鹏丽（1973⁃），女，教授，硕士生导师.

卢鹏丽，E⁃mail：lupengli88＠163.com.