一类特殊幂零李代数的结构

胡建华, 赵卫萍

(上海理工大学理学院,上海 200093)

一类特殊幂零李代数的结构

胡建华, 赵卫萍

(上海理工大学理学院,上海 200093)

鉴于幂零李代数的结构和表示在李理论中有着重要的地位,主要讨论复数域上一类特殊的6维带参数ε的幂零李代数的代数结构.首先,在同构意义下,利用同构的定义及性质,通过大量的推导计算,确定了此类幂零李代数的自同构群同构于6阶矩阵乘法群;其次,探讨了这类幂零李代数的Centroid代数的基本性质,给出了Centroid代数的矩阵表示,同时得出这类幂零李代数的Centroid代数是一个6维幂零李代数;最后,给出了该类幂零李代数的δ-导子的矩阵表示.特别当δ为1时,探讨了该类幂零李代数的导子代数的结构,得出导子代数是10维李代数,外导子代数是5维李代数.

李代数;幂零;自同构;δ-导子

幂零李代数是李理论中一类重要的李代数,其结构和表示在李理论中有着重要的地位.幂零李代数因其结构的复杂性还有很多问题尚未解决,受到许多学者的关注,低维幂零李代数成为学者们探索的对象.Schneider[1]通过确定基的方法给出了低维幂零李代数的分类;Graaf[2]利用中心扩张的方法给出了特征不为2的小于等于6维的幂零李代数的分类;杨恒云等[3]确定了二上同调群的结构.本文在此基础上,研究复数域上一类6维带参数的幂零李代数的代数结构.

1 概 念

定义1[4]设L是域F上的向量空间,在L中定义了一个李括号积(记为[·,·]),对∀x,y∈L,有[x,y]∈L,且以下三个条件成立,称L为域F上的一个李代数.

a.李括号积是双线性的;

b.[x,x]=0,∀x∈L;

c.[x,[y,z]]+[y,[z,x]]+[z,[x,y]]= 0,∀x,y,z∈L(Jacobi等式).

由条件b易得,当Char F≠2时,有[x,y]= -[y,x],∀x,y∈L.

例1[5]对结合代数A,∀a,b∈A,定义运算[a,b]=ab-ba,则A构成一个李代数.

定义2[6]设L是域F上的李代数,{Li}(i≥ 0)为L的降中心列.若存在自然数n∈瓔,使得Ln={0},则称L为幂零李代数.

采用文献[2]的记号,L6,21(ε)表示复数域瓘上这样一个6维李代数,其基为{x1,x2,…,x6},其李括号积为

其余的李括号积[xi,xj]=0.这是一个带参数ε∈瓘的幂零李代数,且L5={0},x6是中心元,并且由文献[2]知,对参数η∈瓘,L6,21(ε)≅L6,21(η),当且仅当存在α∈瓘,使得η=α2ε.本文将刻画复数域上李代数L6,21(ε)的自同构群、Centroid代数、导子代数以及δ-导子.

2 自同构群

定义3[4,7]设L是复数域瓘上的李代数,若线性变换φ:L→L满足

则称φ是L的同态映射,L的所有同态映射的集合记为End(L).若φ是可逆线性变换,则称φ是L的自同构映射,L的所有自同构映射构成一个群,称为L的自同构群,记作Aut L.

定理1 李代数L6,21(ε)的自同构群Aut L6,21(ε)同构于6阶矩阵乘法群

3 Centroid代数

定义4[4,10]设L是复数域瓘上的李代数,若线性变换σ∈End(L)且

记E表示6阶单位矩阵,Eij表示第i行第j列的元素为1,其余元素均为0的6阶矩阵.

定理2 李代数Cent(L6,21(ε))同构于6阶矩阵代数

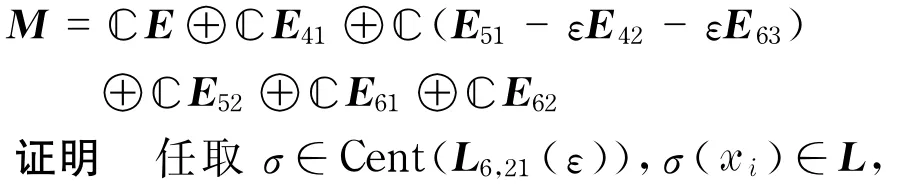
推论1 李代数Cent(L6,21(ε))是幂零李代数,且其维数是6.

证明 由定理2可知,Cent(L6,21(ε))同构于矩阵代数M,而M由对角线元素全相等的下三角矩阵生成,从而M是幂零的,故Cent(L6,21(ε))是幂零的且维数等于M的维数,为6.

4 δ-导子

定义5[6]设L是域瓘上的李代数,若线性变换D:L→L,满足D([x,y])=[D(x),y]+[x,D(y)],∀x,y∈L则称D为L的导子,L的所有导子所成的集合记为Der(L).

性质3[6]设L是域瓘上的李代数,Der(L)是一个李代数.

由文献[4],对∀x∈L,伴随算子ad x∈Der(L),称为L的内导子.L的所有内导子的集合记为Ad(L),构成L的内导子代数.商代数Der(L)/ Ad(L)称为外导子代数.

定义6[13]设L是域瓘上的李代数,δ∈瓘为任意不为零的数,若线性变换D:L→L,满足

[1] Schneider C.A computer-based approach to the classification of nilpotent Lie algebras[J]. Experimental Mathematics,2005,14(2):153-160.

[2] de Graaf W A.Classification of six-dimension of nilpotent Lie algebras over fields of characteristic not 2[J].Journal of Algebra,2007,309(2):640-653.

[3] 杨恒云,叶鑫.两类6维幂零李代数的上同调群[J].上海海事大学学报,2012,33(1):91-94.

[4] Humphreys J E.Introduction to Lie algebras and representation theory[M].New York:Springer-Verlag,1972.

[5] 苏育才,卢才辉,崔一敏.有限维半单李代数简明教程[M].北京:科学出版社,2008.

[6] 孟道骥.复半单李代数引论[M].北京:北京大学出版社,1998:110-115.

[7] Coelho SP.The automorphism group of a structural matrix algebra[J].Linear Algebra and Its Applications,1993,195:35-58.

[8] 胡建华,刘国华.有限域上型A1的Chevalley群之间的同态[J].上海理工大学学报,2009,31,(4): 307-310.

[9] Varadarajan V S.Lie Groups,Lie algebra and their representations[M].Beijing:Collaege Press,1998: 49-67.

[10] Allison B,Benkart G,Gao Y.Central extensions of Lie algebras graded by finite root system[J]. Mathematische Annalen,2000,316(3):499-527.

[11] CicalòS,de Graaf W A,Schneider C.Six-dimensional nilpotent Lie algebras[J].Linear Algebra and its Applications,2012,436(1):163-189.

[12] 许成苏,胡建华.四阶双曲型Kac-Moody代数的极小虚根[J].上海理工大学学报,2013,35(6):531-535.

[13] Zusmanovich P.Onδ-derivation of Lie algebras and superalgebras[J].Journal of Algebra,2010,324: 3470-3486.

[14] Leger G F,Luks E.On derivations and holomorphs of nilpotent Lie algebras[J].Nagoya Mathematical Journal,1971,44:39-50.

[15] Skjelbred T,Sund T.Sur la classification des algèbres de Lie nilpotentes[J].Academy des Science Paris Series,1978,286(5):1-2.

(编辑:董 伟)

Structure of a Certain Class of Nilpotent Lie Algebras

HUJianhua, ZHAOWeiping
(College of Science,University of Shanghai for Science and Technology,Shanghai 200093,China)

The structure and representation of nilpotent Lie algebra play an important role in the Lie theory.The algebraic structure of a certain class of six-dimensional nilpotent Lie algebras with the parameterεover the complex field was discussed.It is determined that in the sense of isomorphism,the automorphism group of this class of six-dimensional nilpotent Lie algebra is isomorphic to a six-order matrix multiplication group by using the definition and properties of isomorphism and a large amount of calculation.Then the properties of Centroid algebras of this class of six-dimensional nilpotent Lie algebra were analysed and its matrix representation was given.It is shown that the Centroid algebra is a six-dimensional nilpotent Lie algebra.Finally,the δ-derivation of this class of six-dimensional nilpotent Lie algebras was determined.Especially in the case ofδ=1,the structure of derivation algebras was discussed and it is concluded that the derivation algebra is a ten-dimensional Lie algebra and outer derivation algebra is a fivedimensional Lie algebra.

Lie algebra;nilpotent;automorphism;δ-derivation

O 152

A

1007-6735(2015)03-0215-05

10.13255/j.cnki.jusst.2015.03.003

2014-04-15

国家自然科学基金资助项目(11201299)

胡建华(1978-),女,讲师.研究方向:代数群及其表示理论.E-mail:smilydragon2011@163.com

��编号:1007-6735(2015)03-0220-05 DOI:10.13255/j.cnki.jusst.2015.03.004