线性调频超声信号脉冲压缩的实时实现

曹玉龙, 郑 政

(上海理工大学医疗器械与食品学院,上海 200093)

线性调频超声信号脉冲压缩的实时实现

曹玉龙, 郑 政

(上海理工大学医疗器械与食品学院,上海 200093)

编码脉冲在不增大发射峰值功率的前提下,通过增大时宽-带宽积显著提高超声平均发射功率,然后在接收端通过脉冲压缩恢复应有的纵向分辨力,并显著增强信噪比.利用现场可编程门阵列(field programmable gate array,FPGA)设计了一个中心频率为10 MHz的线性调频脉冲(chirp)发射和实时脉冲压缩系统,由FPGA控制DDS(direct digital synthesizer)产生chirp信号,送入模拟乘法器与窗函数相乘,经功率放大后作为发射脉冲,回波信号送回FPGA进行脉冲压缩处理,82μs的回波数据可以在230μs的时间里处理完毕.实验使用了中心频率10 MHZ、带宽7 MHZ、时长5μs的chirp信号.和单脉冲系统相比,在纵向分辨力没有明显损失的情况下,脉冲压缩方法使信噪比增强了12.8 dB,旁瓣抑制可以达到30.6 dB.

编码激励;解码压缩;线性调频脉冲;现场可编程门阵列

超声成像的分辨能力与超声频率成正比,但衰减也随频率的升高而增加.由于超声的发射峰值功率受到安全性的限制,因此分辨力和探测深度是一对矛盾.编码脉冲在不增大发射峰值功率的前提下,通过增大时宽-带宽积(TBP)提高平均发射功率,然后在接收端通过脉冲压缩恢复应有的纵向分辨力,这是解决上述矛盾的一个有效方法[1-8].用于脉冲压缩的编码方式有很多种,在超声成像系统中,由于存在衰减所引起的频率偏移,所以具有脊形模糊函数的线性调频脉冲(chirp)是一种理想的方式[4].

本文利用现场可编程门阵列(field programmable gate array,FPGA)实现了一种中心频率为10 MHz的实时线性调频编码脉冲压缩系统.该系统的纵向分辨力和10 MHz单脉冲系统相当,但是与后者相比信噪比增加了12.8 dB,同时,旁瓣抑制可以达到30.6 dB.该系统每次发射后以50 MHz的采样率采集82μm的回波射频信号,脉冲压缩算法在230μs内完成.该系统可以满足帧频20帧/s、每帧图像200线的浅表器官B型超声波扇形扫描仪的实时性要求.

1 线性调频编码的脉冲压缩

传统的单脉冲激励方式中,由于超声波最大发射功率的限定,因而无法通过增加其幅值的方法度来增强激励的能量.如果发射一个编码宽脉冲,则总能量可以显著增加,同时在接收端用匹配滤波器对回波信号进行滤波,就能压缩输出一个单峰信号,如图1所示.

图1 线性调频编码激励系统和单脉冲系统的比较Fig.1 Comparison of chirp coded system with single pulse system

1.1 发射脉冲

线性调频脉冲信号ψ(t)表示为

式中,t表示时间;j表示虚数单位;fl表示信号的起始频率;T表示脉冲宽度;B表示频带宽度.

瞬时频率fi(t)是相位函数的微分,表示为

很明显,在脉宽T内fi(t)线性地扫过了整个带宽B.

复信号ψ(t)的实部作为激励信号η(t)加载到换能器上,则

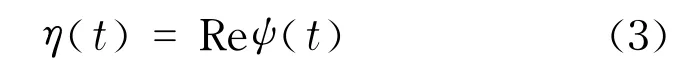
本文采用的换能器中心频率为9.76 MHz, -6 dB带宽为6.29 MHz,故线性调频激励的中心频率设置为10 MHz,带宽为7 MHz.由于本系统应用于浅表器官,为了不使探测盲区过大,脉宽T设计为5μs.

1.2 压缩滤波器

脉冲压缩滤波器(pulse compression filter, PCF)是一个匹配滤波器,表示为

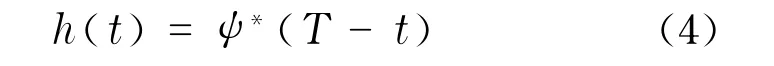
式中,h(t)是脉冲压缩滤波器的冲激响应,是激励信号的共轭、翻转并时移.

脉冲压缩滤波器的输出γ(t)为

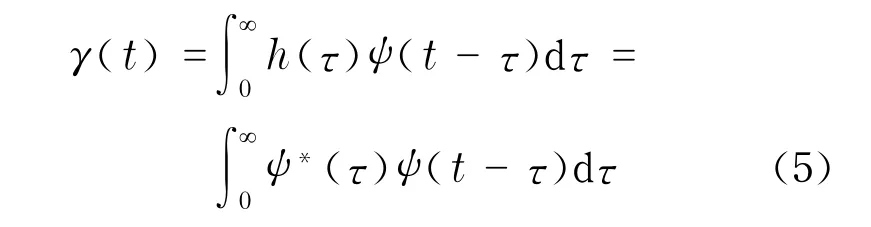
式中,τ表示积分运算中代表时间的中间变量.将式(1)代入式(5),得

当滤波器的输入是实际回波信号时,其数据长度远大于压缩滤波器的长度,可以利用卷积的重叠相加法来实现[9].

根据卷积定理,式(5)可以变换为

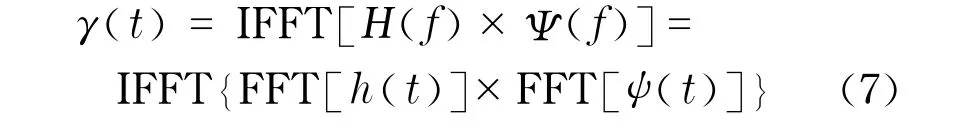
式中,FFT表示快速傅里叶变换;IFFT表示快速傅里叶逆变换;f表示频率.利用FFT和IFFT可以大大减小运算量,提高处理速度.

由于匹配滤波器的输出在频谱上近似一个矩形,所以输出波形时域上存在较大的旁瓣,这会严重影响成像效果.为匹配滤波器加上适当的窗函数可以减小旁瓣,本文采用了切比雪夫窗(Chebyshev)[5].

1.3 菲涅尔纹波及其改善

矩形包络的线性调频信号在时域上两端的突变性导致其频谱上产生菲涅尔波纹,该波纹会导致远端旁瓣的产生.为此,对发射信号在时域上加窗使信号两端渐变(tapering)以削弱菲涅尔波纹,进而削弱远端旁瓣.本文采用的是占时比为0.2的图基窗(turkey)[5],波形如图2所示,纵坐标A表示电压幅度.

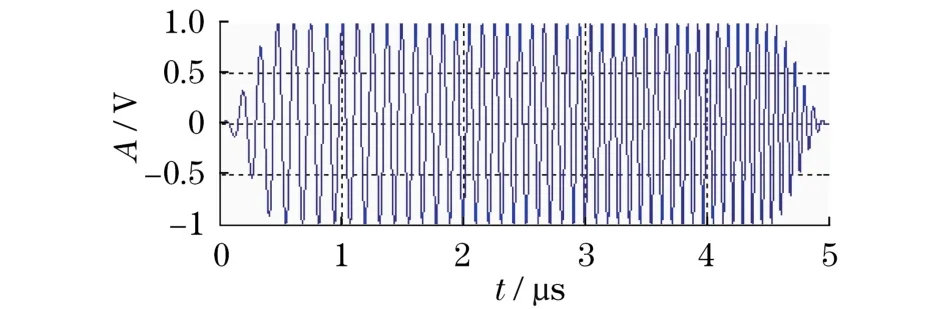
图2 对线性调频激励时域加窗Fig.2 Tapering the chirp excitation

2 脉冲压缩电路

2.1 整体构成

线性调频脉冲压缩系统如图3所示.脉冲发射和压缩电路由同一个同步脉冲控制.DDS(direct digital synthesizer)在这个同步脉冲的控制下产生chirp信号,同时幅度控制电路将事先存储在ROM中的窗函数数据读出,通过DAC(数模转换器)转换为模拟信号.两路信号经过模拟乘法器相乘后得到窗函数加权的chirp信号,该信号经功放后激励超声换能器.

图3 线性调频脉冲压缩系统构成Fig.3 Diagram of chirp pulse compression system

回波信号经过BPF(带通滤波器)并经ADC(模数转换器)采样进入FPGA中.本系统采样率为50 MHz,在线性调频信号的低频端(6.5 MHz)每周期可以采集到约7.7个点,高频端(13.5 MHz)可以采集到约3.7个点.回波信号共采集4 096个点,时长82μs,对应探测深度63 mm.考虑到超声信号的动态范围,本系统采用了12 bit的ADC.

2.2 脉冲压缩电路

脉冲压缩电路如图4所示.

图4 脉冲压缩框图Fig.4 Block diagram of pulse compression process

图4中,u(n)表示数字回波信号,n表示离散时间点.u(n)和互相正交的两个参考信号相乘,经过FIR低通滤波器(LPF)后得到复信号x(n)= xI(n)+j xQ(n),下标I表示实部,Q表示虚部.经过处理的信号频谱下移,所以可以采用隔二取一的方法进行降采样,采样率降低为25 MHz,回波信号的数据长度缩短为2 048点.将同相项和正交项分别存在两个双口RAM中,等待压缩处理.

压缩滤波器的冲击响应是通过激励波形ψ(n)变换得到的,所以可以事先计算其参数供处理时使用.按照图4中虚框内的计算步骤,将与发射脉冲相同的信号在50 MHz的频率下抽样,得到250个点,经过和上文相同的步骤获取复数信号并降采样,得到两个125点的相互正交的信号.将它们进行时移、反转、取共轭、加窗,并进行傅里叶变换,即获得压缩滤波器的频域响应函数H(k)=HI(k)+j HQ(k),k表示离散频率点.

将降频后的回波信号均匀分割为16段, x1(n),x2(n),…,x16(n),每段128点,与压缩滤波器h(n)长度接近,分别和滤波器系数作卷积运算,则yi(n)=h(n)xi(n),其长度为252点.其中,y1(n)的后124点和y2(n)的前124点、y2(n)的后124点和y3(n)的前124点……对应相加才是该部分卷积的正确值,与其它值组合,一起构成最终的卷积结果,如图5所示.

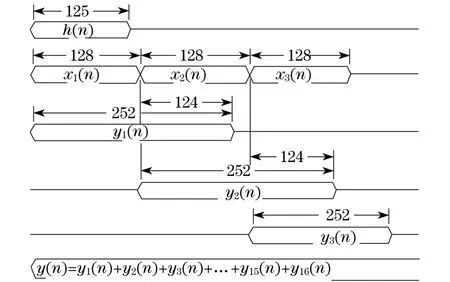
图5 卷积的重叠相加法Fig.5 Overlap-adding algorithm of convolution

利用卷积定理将上述分段信号的卷积yi(n)= h(n)xi(n)转换到频域进行运算.先对h(n)及xi(n)补零到N点,N大于等于252,一般选取N= 2D(D为整数),故N取256.如上文所述,回波信号经过正交解调后同相项和正交项分别存在两个双口RAM中,按照每次128点的方式将两路信号读出并送入复数FFT IP核的两个输入端,经转换后获得回波信号的傅氏变换X(k)=XI(k)+j XQ(k).本系统所使用的Altera公司的FFT IP核支持4种I/O数据流结构,在速度满足的前提下,使用占用资源最少的突发类数据流结构,每次运算约8.2μs.将FFT后的结果与预先存在ROM中的压缩滤波器系数频域响应函数H(k)相乘.由于该乘法是复数乘法,故使用了4个乘法器,分别计算XI×HI,XI× HQ,XQ×HI和XQ×HQ,然后用XI×HI减去XQ× HQ,得到同相分量YI,用XI×HQ加上XQ×HI,得到正交分量YQ.上述结果进行快速傅氏反变换IFFT,得到每段的卷积结果yi(n).

将分段运算的结果按上文所述的方法重组,即得到整个回波的压缩滤波结果.

回波信号经过压缩滤波器之后得到的是一个复信号,包括同向分量I和正交分量Q.将I分量和Q分量分别平方,然后相加取二次方根就得到了包络信号.本设计采用流水线型的非冗余开方算法[10],其占用逻辑单元少,计算时间短,且不需要调用乘法器.

3 实验及分析

3.1 实验设计

本系统作为B型扫描仪的一部分,其输出是数字形式的包络信号,为便于实验,专门增加了一个数模转换器DAC,将此数字信号转换成模拟量,以便利用示波器实时观察.经模拟放大的回波信号送到示波器的另外一个通道,和处理结果同时观察.另外,还利用FPGA设计工具QUARTUS II中的SignalTap软件[11-13]抓取数据并进行离线分析.

实验1以一根直径为0.08 mm金属细丝为靶目标,将换能器探头在水介质中对准靶目标,利用示波器同时观察回波及处理结果.

实验2以一个有机玻璃方盒作为靶目标,将换能器垂直对准方盒的上盒壁,如图6所示,重复上述步骤.该方盒的盒壁厚度L为2.6 mm,盒壁间距为10.2 mm.

图6 以有机玻璃方盒为靶目标Fig.6 Methyl methacrylate box used as the target

3.2 结果与分析

实验1的靶线回波和压缩处理结果如图7(a)和图7(b)所示.靶线回波幅度呈现明显的梭形,这是发射脉冲加权函数和超声换能器频率特性共同作用的结果.回波信号持续了5μs,和发射信号宽度相符,经过滤波后信号宽度压缩为350 ns(-6 dB),相当于10 MHz超声系统的3.5个射频周期.通过对SingnalTap获取的压缩结果进行离线分析可知,主旁瓣信噪比(signal to sidelobe noise ratio,SSNR)为30.6 dB,如图8所示.

由于压缩滤波结果通过运算得到,而且DAC的输出幅度还和参考电压有关,所以在示波器上比较其与回波信号的幅度没有实际意义.为了评估压缩前后信噪比的变化,移去靶目标,在靶线回波出现的位置获取背景噪声,如图7(c)和图7(d)所示,根据式(9)计算信噪比(SNR)[14],即

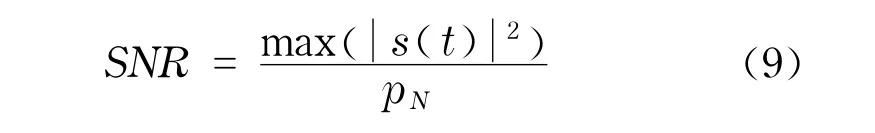
式中,s(t)为信号幅值;pN为噪声平均功率.

图7 压缩前后的波形与噪声Fig.7 Waveforms&noises before and after compression

图8 压缩后的波形Fig.8 Waveform after compression

压缩滤波前,信噪比为43.3 dB,压缩后变为56.1 dB,提升了12.8 dB.

实验2的回波信号及压缩波形如图9所示.可以看见,在回波信号中,有机玻璃方盒盒壁的两个界面的回波是交叠在一起的,而经过脉冲压缩之后,重叠的回波被区分开来.根据超声在有机玻璃和水中的声速[15]计算得到盒壁厚度为2.9 mm,盒壁间距为10.3 mm,和实际值的误差分别为10.3%和1.0%.

图9 实测回波波形(上)与对应的压缩滤波后的波形(下)Fig.9 Echo waveform and corresponding compressed waveform of the plastic box

4 讨 论

实验1中得到的SSNR值为30.6 dB,但是利用实验参数在Matlab中进行仿真,得到的SSNR值却为34.6 dB,比实验结果高4 dB.观察发射脉冲(图7 (a)),可以看到有明显的波形失真,而仿真是基于理想波形的,所以差距可能来自发射脉冲的不理想.实验2中盒壁厚度和盒壁间距都是依据参考资料中给出的材料声速估算出来的,和实际尺寸的误差分别为10.3%和1.0%.由于盒壁的材料是有机玻璃,而盒壁之间是水,通常不同的实验中水的成分不会有太大的差别,而有机玻璃的成分差别较大,所以盒壁厚度的误差可能是由于不同研究所采用的材料差别引起的.

本文实现了基于FPGA的线性调频脉冲发射和压缩系统的设计,满足浅表器官B型超声波扇形扫描仪的实时性需求,系统结构简单,修改方便,便于参数调整.当使用更高带宽的换能器,以及追求深层信号而忽略探测盲区的时候,可以通过增大信号的时宽和带宽的方式,进一步提高信噪比[16]以及增强旁瓣的抑制[5].

[1] Takeuchi Y.An investigation of a spread energy method for medical ultrasound systems.Part one: theory and investigation[J].Ultrasonics,1979,17(4): 175-182.

[2] O’Donnell M.Coded excitation system for improving the penetration of real-time phased-array imaging systems[J].IEEE Transactions on Ultrasonics, Ferroelectrics,and Frequency Control,1992,39(3): 341-351.

[3] Rao N A.Investigation of a pulse compression technique for medical ultrasound:a simulation study [J].Medical&Biological Engineering&Computing, 1994,32(2):181-188.

[4] Misaridis T,Jensen J A.Use of modulated excitation signals in medical ultrasound.PartⅠ:basic concepts and expected benefits[J].IEEE Transactions on Ultrasonics,Ferroelectrics,and Frequency Control, 2005,52(2):177-191.

[5] Misaridis T,Jensen J A.Use of modulated excitation signals in medical ultrasound.PartⅡ:design and performance for medical imaging applications[J]. IEEE Transactions on Ultrasonics,Ferroelectrics,and Frequency Control,2005,52(2):192-207.

[6] Misaridis T,Jensen J A.Use of modulated excitation signals in medical ultrasound.PartⅢ:high frame rate imaging[J].IEEE Transactions on Ultrasonics, Ferroelectrics,and Frequency Control,2005,52(2): 208-219.

[7] Jensen J A.Field:a program for simulating ultrasound systems[C]∥10th Nordic-Baltic Conference on Biomedical Medical&Biological Engineering& Computing,1996,34:351-353.

[8] Behar V,Adam D.Parameter optimization of pulse compression in ultrasound imaging systems with coded excitation[J].Ultrasonics,2004,42(10):1101-1109.

[9] 朱军.数字信号处理[M].合肥:合肥工业大学出版社,2009.

[10] 万明康,陈国军,王大鸣.基于FPGA的开方运算实现[J].数据采集与处理,2006,21(z1):232-235.

[11] 王诚.Altera FPGA CPLD设计(基础篇)[M].北京:人民邮电出版社,2005.

[12] 刘可,徐伯庆,孙国强.基于FPGA的电子提花机控制系统[J].上海理工大学学报,2004,26(2):168-175.

[13] 蒋念平,李伟.现场可编程门阵列实现液晶显示控制的新方法[J].上海理工大学学报,2009,31(2): 190-194.

[14] 周正干,张宏宇,魏东.脉冲压缩技术在超声换能器激励接收方法中的应用[J].中国机械工程,2010,21 (17):2127-2131.

[15] 冯若.超声诊断设备原理与设计[M].北京:中国医药科技出版社,1993.

[16] Machado T M,Costa E T.A comparative study using both coded excitation and conventional pulses in the evaluation of signal to noise ratio sensitivity and axial resolution in ultrasonic A-mode scan[J].Revista Brasileira de Fisica Medica,2011,5(1):35-40.

(编辑:丁红艺)

Real Time Pulse Compression of Chirp Ultrasound Signal

CAOYulong, ZHENGZheng
(School of Medical Instrument and Food Engineering,University of Shanghai for Science and Technology,Shanghai 200093,China)

The coded excitation significantly strengthens the averaged ultrasound power without increasing the peak intensity.The axial resolution can be recovered by pulse compression at the recieving end,and the signal to noise ratio(SNR)can be greatly increased.A FPGA(field programmable gate array)-based real-time chirp pulse compression system with 10MHz central frequency was designed.A FPGA controled DDS(direct digital synthesizer)was applied to generate the tapered chirp signal.This signal was then used as the excitation signal after being magnified by a RF power amplifier.The echo signal was sent back to the FPGA through an ADC and on it the pulse compression was implemented.82μs echo-signal data can be processed up within 230μs.An experiment was done using a chirp excitation with 10MHz center frequency,7 MHz bandwidth and 5μs duration.The results show that the signal to noise ratio is increased by 12.8 dB with slight axial resolution loss,and the sidelobes depression reaches 30.6 dB.

coded excitation;pulse compression;chirp;FPGA

R 318.04

A

1007-6735(2015)03-0295-06

10.13255/j.cnki.jusst.2015.03.017

2014-03-25

曹玉龙(1988-),男,硕士研究生.研究方向:医学超声成像.E-mail:478868101@qq.com

郑 政(1961-),男,研究员.研究方向:生物医学电子学、医学超声成像.E-mail:zheng.bts@gmail.com