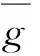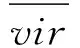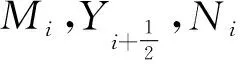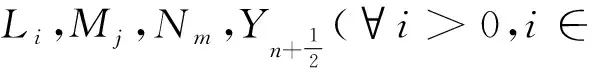一类扩张无限维李代数的子代数
2022-04-18余德民柴嘉潞
余德民, 柴嘉潞, 李 笛
(湖南理工学院数学学院, 湖南 岳阳 414000)
[Fi,Fj]=(j-i)Fi+j(∀i,j∈).

本文研究扩张李代数Schrodinger-Virasoro.这类李代数是Virasoro李代数的推广.Virasoro是以阿根廷物理学家Virasoro的名字命名的一类重要的无限维李代数,Virasoro李代数在数学和理论物理中尤其是共形理论和弦论方面有非常重要的应用.


此运算在基向量上双线性扩张,并满足反对称性和Jacobi不等式,称g为扩张李代数Schrodinger-virasoro.文献[1]研究了Schrodinger-Virasoro扩张李代数的结构,文献[2]研究了Schrodinger-Virasoro的表示.文献[3-7]研究了Virasoro李代数及其推广的Virasoro李代数,文献[8-15]研究了推广的Virasoro李代数的结构分类、导子、自同构和最高权模,以及相关问题.本文研究了这类李代数的子代数、同构.
1 主要结果及证明
定义1设由Li(∀i∈)张成的子空间为g1.
定理1g1是g的无限维非交换李代数.
证明∀i,j∈,可验证
[Li,Lj]=(j-i)Li+j,
从而,g1是g的子代数,g1也是g的无限维非交换子代数.
定理2g1是g的半单李子代数.
证明由于∀i∈Ζ,∀j∈Ζ,Li∈g1,Lj∈g1,
[Li,Lj]=(j-i)Li+j,
g1无二维交换李子代数,反证假设h为g1代数的二维交换子代数,设x,y为h的基,则x≠0,y≠0,设
x=k-mLm+k-m+1L-m+1+…+k-1L-1+k0L0+
k1L1+…+kn-1Ln-1+knLn,
y=l-mLm+l-m+1L-m+1+…+l-1L-1+l0L0+
l1L1+…+ln-1Ln-1+lnLn,
观察矩阵:
(kn,ln不全为零),
因为h为交换子代数,所以
[x,y]=0.
(1)
仔细观察系数矩阵,(1)式左边经过具体计算之后可知L2n-1系数为
同理观察L2n-2的系数
利用行列式有关知识,由于kn,ln不全为0,
同理观察L2n-2的系数
利用行列式有关知识,由于kn,ln不全为零,
从而

于是L2n-3的系数
根据上式,有
又考虑L2n-4系数
利用前述结论有
从前述有
从而有
从前面有
于是有
又考虑L2n-5的系数
利用前面结论有
从而


i1 φ1在g1的基向量Li上线性扩张. φ1([Li,Lj])=[φ1(Li),φ1(Lj)](∀i,j∈), 从同构的意义上说,无中心的Virasoro李代数是无限维李代数Schrodinger-Virasoro的子代数,也可以说无限维李代数Schrodinger-Virasoro的子代数是无中心的Virasoro李代数的推广. 定义2设由Mi(∀i∈)张成的子空间为g2. 定理4李代数g不是单李代数,也不是半单李代数. 证明先证明g2是g的无限维交换子代数,并且g2是李代数g的交换理想.∀i,j∈,由于[Mi,Mj]=0,从而,g2是g的无限维交换子代数,∀m,n∈,由于 [Lm,Mn]=nMn+m,[Mm,Mn]=0, 从而g2是李代数g的交换理想,故原命题成立. 构造g到g映射如下: φ2:g→g,φ2(Li)=10iLi, φ2(Ni)=10iNi,φ2(Mi)=10iMi, 定理5φ2是g到g的同构. 证明从构造知φ2是g到g同构的线性映射,且既是单射.可验证∀i,j,n,m∈, 从而对∀u,v∈g,φ2([u,v])=[φ2(u),φ2(v)],于是φ2是g到g的同构. 定理6g3是g的无限维非交换子代数,且g3是g理想. 证明∀m,n∈,可验证 [Lm,Nn]=nNn+m,[Mm,Nn]=-2Mn+m, 从而,g3是g的无限维非交换子代数,且g3是g理想. 定义4设由Ni,Li(∀i∈)张成的子空间为g4. 定理7g4是g的无限维非交换子代数,且g4不是g理想. 证明∀m,n∈,可验证 [Lm,Ln]=(n-m)Ln+m, [Lm,Nn]=nNn+m,[Nm,Nn]=0. 从而,g4是g的子代数,g4也是g的无限维非交换子代数,且 于是g4不是g理想. 定义5设由 j∈,∀m>0,m∈,∀n>0,n∈) 张成的子空间为g+. 定理8g+是g的无限维非交换子代数. 证明∀m>0,m∈,∀n>0,n∈,可验证 [Lm,Ln]=(n-m)Ln+m, [Lm,Mn]=nMn+m,[Mm,Mn]=0. [Lm,Nn]=nNn+m,[Mm,Nn]=-2Mn+m, 从而g+是g的无限维非交换子代数. 定义6设由 j∈,∀m≥0,m∈,∀n≥0,n∈) 张成的子空间为g0+. 定理9g0+是g的无限维非交换子代数. 证明∀m≥0,n≥0,m,n∈,可验证 [Lm,Ln]=(n-m)Ln+m, [Lm,Mn]=nMn+m,[Mm,Mn]=0. [Lm,Nn]=nNn+m,[Mm,Nn]=-2Mn+m, 从而g0+是g的无限维非交换子代数.显然,g+⊂g0+⊂g. 定理10g+是g0+的无限维非交换子代数,g+是g0+理想. 证明由于g+是g的无限维非交换子代数,当然g+是g0+的无限维非交换子代数.∀m>0,n>0,m,n∈,可验证 [Lm,L0]=-mLm,[L0,Mn]=nMn, [Lm,M0]=0,[Mm,M0]=0, [Lm,N0]=0,[Mm,N0]=-2Mm, 从而g+是g0+理想.