基于最低价中标法的最优投标报价模型

郭林锋, 李秀君, 赵雪美

(1.上海理工大学环境与建筑学院,上海 200093;

2.南京理工大学计算机科学与工程学院,南京 210094)

基于最低价中标法的最优投标报价模型

郭林锋1, 李秀君1, 赵雪美2

(1.上海理工大学环境与建筑学院,上海 200093;

2.南京理工大学计算机科学与工程学院,南京 210094)

为了使施工企业在投标报价时获得最大的中标概率和最高的利润率,结合评标采用最低价中标原则,建立了使中标概率最大、利润率最高的多目标决策模型,并将该模型转换为使期望利润率最大的投标报价模型.根据施工企业的资金问题,以及银行的存款利率和贷款利率,分别给出了在不考虑资金问题、考虑贷款利率和考虑存款利率这3种不同情况下的最优投标报价,以及与之相对应的中标概率和利润率,为具有不同经济实力的施工企业提供了投标依据.最后对模型的结果进行了合理的分析,得出了最优投标报价主要由施工企业的工程成本所决定.

投标报价;最低价中标;中标概率;利润率

随着我国建设项目投资的不断扩大,建设工程招投标制度使用的范围越来越广,招标已成为我国建设工程施工发包的主要形式.在整个招投标过程中,评标方法起着关键性的作用,评标方法选择的不同,中标的结果也大不相同.

工程招标的评标方法多种多样,各个国家规定的评标方法也大不相同.美国近百年来一直采用唯一的评标方法:最低价中标法[1].我国招标投标法规定的两种评标方法为综合评估法和经评审的最低价法[2].前者是将各项评价指标量化,由评标专家对各投标人进行打分,得分最高者中标;后者是在技术标和有关方面达到要求的情况下,被评标委员会认为合理的最低报价人中标.

近年来最优投标报价问题的研究取得了一系列丰硕的成果,评标采用经评审的最低价法可以应用概率分布法[3-4]、博弈理论[5-7]等方法确定最优报价.贾长麟[8]综合考虑中标率和盈利,建立了一个投标报价模型并利用微分知识求解,分析了投标报价与企业成本、招标控制价以及投标报价之间的关系,确定最优投标报价.蓝筱晟[9]通过对投标报价进行博弈分析,将投标过程看作是博弈行为,构建出最低价法下的博弈模型,进而得到最优解.本文在前人研究的基础上,主要针对评标采用最低价法,研究建设工程的最优投标报价模型.

1 模型的假设与分析

1.1 模型的假设

a.参加投标的企业都符合招标文件中的资质要求,且相互独立,无信息沟通,更不会出现围标现象.

b.投标单位所雇用的造价人员熟悉工程量清单规范,制作的标书无原则性错误,即不会产生废标.

c.招标人给出的最高招标控制价准确合理,能够反映工程实际情况,最低招标控制价可根据招标具体情况确定.

d.投标报价能够看作连续的随机变量,且在区间[a,b]上服从线性分布,其中,a,b分别为招标最低和最高控制价.

e.评标遵循公开、公平和公正原则,且采用“最低价中标”的评标原则.

1.2 模型的分析

施工企业在投标时主要考虑是否能中标以及中标后能否给企业带来效益.由于投资所产生的利润率能够反映企业资金的增值能力[10],因此,可以通过利润率的大小来评价施工企业参与投标的价值.当招标单位采用最低价进行评标时,施工企业在投标过程中,为了使中标的概率最大,往往会压低投标报价,但过度压低报价又会导致中标后利润率减少,甚至导致企业的亏损.由此,合理的投标报价对企业的发展至关重要.施工企业在确定投标报价的过程中,既要使中标的概率较大,又要使利润率较高.因此,在评标采用最低价中标规则下,可以以中标概率最大、利润率最高为目标,建立最优投标报价模型.

2 模型的建立与求解

2.1 模型的建立

根据最低价中标原则,若有n家单位参与投标,且单位i的投标报价t为中标价,则其它没有中标的n-1家单位的投标报价均在区间(t,b]内.因此,以中标价t作为投标报价的单位i,其中标概率为

式中,t为中标价;b为招标最高控制价;n为投标单位的数目;tj为单位j的投标报价;f(tj)为单位j投标报价的密度函数.

根据假设条件d,投标报价在区间[a,b]上服从线性分布,则单位i的中标概率为

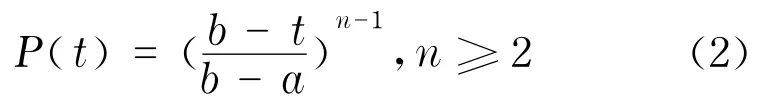
根据施工图或业主提供的清单工程量,施工单位可以按照企业内部定额编制施工预算,由此可以估算得出承包该工程所需的施工工期,以及预算得出完成该工程所需的工程成本.其中,成本是企业作出决策的重要信息[11].

若单位i中标,即投标报价t为中标价,考虑单位i所需的施工工期T和工程成本c,则投资工程成本c给该单位带来的利润率为

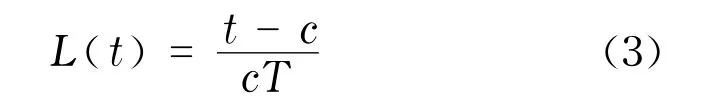
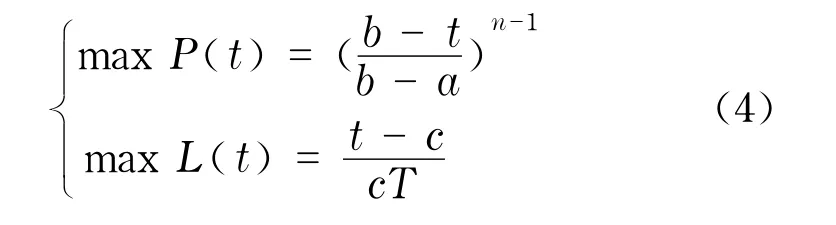
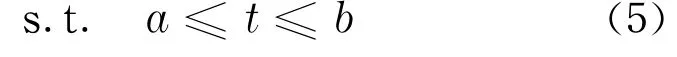
为使施工企业的中标概率和利润率最大,可以建立模型I,即由于该问题有两个决策目标,因此所建立的模型I属于多目标决策模型.由于多目标决策问题客观存在着两个基本特点:目标间的矛盾性和目标间的不可公度性[12],因此,多目标决策问题一般不存在通常意义下的最优解,即不存在既满足约束条件,又能使所有的属性分别达到各自的最优值.于是,一般情况下,只能寻求问题的非劣解.

模型转换后,变为求解期望利润率的最大值.该模型II的最优解即为模型I的非劣解,经过上面的转换,使得多目标决策模型的非劣解具有实际意义.

2.2 模型的求解

2.2.1 不考虑资金问题

当不考虑施工单位的资金问题时,即对投标报价t没有其它约束条件进行限制时,对上面模型II中的f(t)进行求导,可得

2.2.2 考虑贷款利率

当施工企业遇到资金问题时,通常情况下企业都是向银行进行贷款的.如果投资产生的利润率比贷款利率还低,一旦施工企业遇到资金问题,就会出现亏损.因此,在投标过程中,资金不够雄厚的施工企业还需考虑各银行的最低贷款利率.

为了使投资产生的利润率高于最低贷款利率,模型II中的约束条件由a≤t≤b变为t′≤t≤b,其中,t′=(1+rT)c,即模型II变为

2.2.3 考虑存款利率

对于有大量流动资金的施工企业来说,如果投资产生的利润率比最高存款利率还低,施工企业仅从经济方面来看,就没有必要进行投标.因此,在投标过程中,资金雄厚的施工企业还需考虑各银行的最高存款利率.

3 模型的结果与分析

4 结 论

本文主要通过中标概率和利润率来分析在最低价中标规则下的最优投标报价问题.为了使施工企业的中标概率最大和利润率最高,建立了一个多目标决策模型,并将该模型转换为使期望利润率最大的投标报价模型,进而得出具有实际意义的非劣性解.结合考虑施工企业的资金问题,以及银行的存款利率和贷款利率,对所建模型中的约束条件进行了相应的改变,得出在不考虑资金问题、考虑贷款利率和考虑存款利率这3种情况下的最优投标报价,以及按这些投标报价进行投标企业的中标概率和利润率.施工单位可以根据自身经济实力,借鉴本文所建立的模型得出最优投标报价.

当评标采用最低价评标原则时,运用本文所建立的最优投标报价模型能够使施工单位的中标率较大、利润率较高.通过对模型的结果进行分析,可以看出施工企业要想在今后的投标过程中以较大的优势胜出,应加强企业自身的成本管理,努力提高企业的核心竞争力.

[1] 吴福良,胡建文.中美建设工程施工招标方法比较研究[J].建筑经济,2001(7):11-13.

[2] 贾长麟.对最低价中标评标方法的信息经济学分析[J].建筑经济,2008(5):76-78.

[3] Friedman L.A competitive-bidding strategy[J]. Operations Research,1956,4(1):104-112.

[4] Gates M.Bidding strategies and probabilities[J]. Journal of the Construction Engrg.Division,ASCE, 1967,93(1):75-110.

[5] Riley JG,Samuelson W F.Optimal auction[J].The American Economisc Review,1981,71(3):381-392.

[6] 敬辉蓉,李传昭.建筑工程最低价中标博弈机制研究[J].科技管理研究,2007(5):113-115.

[7] 饶海琴,徐彩红.政府投资项目中的不完全信息静态博弈模型分析[J].上海理工大学学报,2006,28(4): 386-390.

[8] 贾长麟.最低价中标规则下企业最优投标报价研究[J].武汉理工大学学报(信息与管理工程版),2010, 32(3):490-493.

[9] 蓝筱晟.最低价中标法的投标博弈研究[J].价值工程,2011,30(15):75-76.

[10] 冯红霞.对投资利润率指标的分析[J].财会月刊, 1999(10):19-20.

[11] 樊一阳,侯建明.成本测量与企业决策[J].上海理工大学学报,2001,23(1):66-70.

[12] 韩中庚.数学建模方法及其应用[M].北京:高等教育出版社,2005.

(编辑:丁红艺)

Optimal Bidding Model Based on the Rule of Lowest Price Successful Bid

GUOLinfeng1, LIXiujun1, ZHAOXuemei2
(1.School of Environment and Architecture,University of Shanghai for Science and Technology,Shanghai 200093,China; 2.School of Computer Science and Engineering,Nanjing University of Science and Technology,Nanjing 210094,China)

In order to get the biggest bid winning probability and margins for construction enterprises when bidding,a multi-objective decision model was proposed by combining the principle of lowest bid which can achieve the largest successful bidding probability and the most profitability. Moreover,the above model was converted to a bid model which can maximize the expected profit margins.According to the problems of funds for construction enterprises,bank deposit rates and lending rates,optimal bidding price models were respectively given in the three cases of without thinking about the money,considering lending rates and considering deposit interest rates.Besides, the corresponding winning probability and profit margins were also presented providing a bidding basis for construction enterprises with different economic strength.The models and results,after analysis,show that the optimal bidding price is mainly determined by the engineering cost.

bid price;lowest price bid;successful bidding probability;profitability

TU 723.2

A

1007-6735(2015)03-0274-05

10.13255/j.cnki.jusst.2015.03.013

2014-03-19

郭林锋(1988-),男,硕士研究生.研究方向:建筑经济与建筑项目管理研究.E-mail:glfgchsh@126.com

李秀君(1976-),女,副教授.研究方向:沥青路面材料、机械化养护技术、项目管理研究等.E-mail:junzixiu@163.com