基于有限元分析的机油泵卡死现象设计改进

杜宝江, 丁鹏鹏, 于亚君, 陈宇翔

(上海理工大学机械工程学院,上海 200093)

基于有限元分析的机油泵卡死现象设计改进

杜宝江, 丁鹏鹏, 于亚君, 陈宇翔

(上海理工大学机械工程学院,上海 200093)

针对机油泵在试生产中遇到的卡死现象进行分析.利用有限元分析软件Ansys,结合实际经验,采用了一种更全面的分析方法,得到机油泵在极限实验状态下的相关分析数值,找出造成卡死的主要因素为从动轴和从动齿轮的尺寸公差设计不合理.根据此原因,采取相应的方法进行设计改进,并通过实验对改进方案进行验证,最终证明了分析结论的合理性.

机油泵;卡死;Ansys软件;故障分析;设计改进

机油泵是汽车发动机的重要组成部件之一,其保证机油在润滑油路中不断循环.某汽车配件公司在对设计的试生产机油泵进行极限条件(转速6 500 r/min、油温140℃)实验过程中发现,约有25%的机油泵会出现从动部分卡死现象,从动齿轮不能绕从动轴转动,直接导致机油泵无法正常工作.本文对此卡死现象进行分析研究.

我国在泵类机械方面的设计能力相对薄弱,主要是参照国外的设计经验,进行理论分析少.近几年国内也开始重视将有限元技术应用到机油泵产品的设计中去,但是,主要集中在对机油泵内流场或者结构强度的分析上,忽视了诸如油膜厚度等因素在机油泵设计中的影响.本文基于对产品故障分析的基础上,结合实际经验,利用有限元分析软件Ansys对内流场方面进行了计算,并以润滑油膜的分析作为重点,综合地剖析机油泵的运行状况,找出故障原因,同时也为机油泵有限元设计改进提供了一种新的思路.

1 有限元分析方法

本文研究的机油泵为齿轮式机油泵,从动齿轮与从动轴的配合为间隙配合,其结构如图1所示.机油泵在运转状态下,不同位置的油压不同,导致力的不平衡,从而造成从动齿轮发生侧移,并且从动齿轮受到驱动齿轮传递的驱动力,进一步加剧了从动齿轮的各个方向上的受力不均.除此之外,机油温度的变化也是影响机油泵各部分变形的一个重要因素,这些都可能导致部件之间接触磨损.根据机油泵的工作原理以及对故障实物的初步分析,得出可能影响机油泵卡死的主要因素为温度和油压,以此作为研究方向进行分析.

图1 机油泵机构图Fig.1 Structure of oil pump

机油泵的分析涉及流场、温度场及受力等多方面因素[1].在实际的运算过程中,很难将所有情况在同一个模型中同时进行分析.本文采用先单一要素分析后将各要素综合处理的分析思路,首先进行流固耦合的内流场计算,得到油腔内压力的分布状况,进而将压力结果作为条件应用到热力耦合的计算中,最终实现对机油泵的全面分析.

1.1 内流场分析

采用Ansys中CFX模块的流固耦合方法对机油泵的流场作数值模拟分析.在对内流场进行分析之前,应首先确定机油泵内部流体的流动状态,而雷诺数Re是判断流体流动状态的一个重要参数.式中,v代表流体的平均流速;D代表水力直径;γ代表流体的运动黏度.

从数值上对流体流动状态进行分析,当雷诺数Re≤2 300时,流体的流动为层流流动;当雷诺数Re≥4 000时,流体的流动为湍流流动;而当2 300＜Re＜4 000时,流体的流动介于层流流动与湍流流动的过渡区间.根据式(1)计算可得,本文所研究的机油泵内部流动雷诺数远大于湍流流动的临界雷诺数4 000,所以,机油泵内流场的流动为复杂的湍流状态[2].

a.流体计算域边界条件.

软件中流体的属性参照实际机油的相关参数进行设置,参考压力为101 kPa.由于标准k-ε模型对所有的流动问题都有比较好的普适性,对于多数流动类型来说,它的精度都处于多种湍流模型的中游水平,并且其收敛性比多数湍流模型要好,计算速度也稍微快一些,因此,Turbulence选项中选择k-ε模型[3].k为湍动能,ε为湍流耗散率.

b.固体计算域边界条件.

对于齿轮转子来说,在Ansys Workbench软件的Basic Settings选项中,选择计算域的类型为侵入式固体域,另外,给定转速r=6 500 r/min.

c.其它条件的设置.

对于机油泵内流场与壳体相接触的固定壁面设置为无滑移、光滑、绝热的壁面.模拟过程中机油恒温,为140℃.湍流动能、动能耗散项、动量方程均采用二阶迎风格式离散.在进行迭代计算时,迭代方式选择亚松弛迭代[4].湍流模型采用k-ε模型,控制方程采用Navier-Stokes方程,压力速度耦合采用SIMPLE算法[5].

内流场的分析结果反映出机油泵在运行时作用于不同齿轮面的油压和流速大小有所差异,如图2和图3所示,这就需要在后续热力耦合分析时,针对不同的受力面设置不同的油压参数,而各受力面的油压具体数值通过上述分析结果获取.

为验证内流场分析结果的可靠性,对机油泵出口油压以及出口流量进行实验,将得到的实验数据与分析数据进行对比,比较结果如表1所示.实验数据与分析数据的偏差较小,故对内流场的分析过程合理,分析结果接近真实值.

1.2 热力耦合分析

在分析的过程中,采用了适当的假设来简化计算,同时利用参数化方法,缩短变量频繁设置的时间,提高自动化程度.

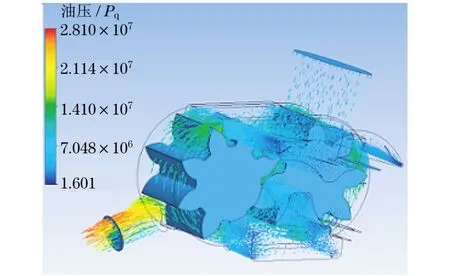
图2 机油泵油压分布云图Fig.2 Hydraulic contours of oil pump

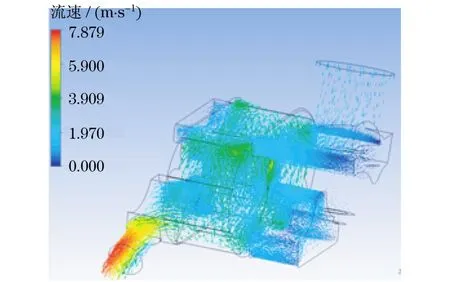
图3 机油泵流速分布云图Fig.3 Velocity of oil chamber

表1 仿真数据与实验数据比较表Tab.1 Comparison table of experimental data and analytical data

1.2.1 模型的简化

根据圣维南原理对模型进行适当简化,去除一些倒角以及泵体多余部分.对于像圆柱、圆环等结构,在网格划分时网格形状往往比较错乱,为解决这一问题,在对网格进行划分前将模型进行分块处理,处理后的网格划分结果如图4所示.由相关的研究得知,机油泵在运转过程中可将从动齿轮与从动轴之间的油膜视为具有一定的刚度,能够承受比较大的径向力,而且随着转速的增大,油膜能承受的径向力也增大,在承受同样载荷的情况下,发生的偏移量也会变小[6].针对油膜的这一特性,在分析时将油膜模型简化,在两配合面间添加一弹性模量较大弹簧条件来模拟油膜的作用.

1.2.2 间隙配合的设置

图4 网格划分Fig.4 Gird distribution

在Ansys软件中,模型间的间隙量和过盈量的设置通常有两种方法.一种是通过将配合条件设置为frictional模式来设置,其中,参数offset的数值即为相应的间隙量和过盈量的值.另一种方法是在模型建立时,直接通过尺寸上的数值设定来反映模型间的间隙量和过盈量.相比第二种方法,第一种方法不需要在建模时考虑公差的问题,能够通过修改offset中的数值方便地调整间隙量,省去了重新修改模型的时间,而且计算结果的准确性更高.

1.2.3 温度场的设置

根据相关文献及部分实验数据,从动轴与从动齿轮的间隙为0.014 mm,取油膜温度为220℃,以此为参考,采取适当的函数关系来反映正常运行时的油膜温度与原始油膜厚度的关系,进行参数化设置.油腔内的油温则取极限工作状态下的140℃,泵体表面的对流换热系数设置为1 500 W/(m2·℃).温度场的分析结果如图5所示,由于从动轴与从动齿轮存在高速的相对旋转,而且与机油接触部分较少,散热条件差,所以,从动轴的温度相对于其它结构的温度也较高.

图5 从动部分温度场Fig.5 Temperature distribution of driven part

1.2.4 油压及扭矩的设置

油压在前面内流场的分析中已经得到,仅需要将其添加到从动齿轮上即可.通过实验得到驱动轴所受的扭矩T=2.38 N·m.根据材料力学知识,驱动齿轮带动从动齿轮匀速转动视为驱动齿轮在啮合点给从动齿轮一个与输入扭矩大小相等的力矩T1,即

式中,F为啮合点受到的垂直于啮合表面的力;t为通过F方向的直线与从动齿轮中心的垂直距离[5].

代入相应的t,可计算得啮合力F=151.11 N.

2 结果分析

2.1 数据分析

从图6变形结果的矢量图可以看出,在温度升高的影响下,从动轴和从动齿轮都发生热膨胀,而且从动部分上端面没有约束,所以,向上的变形量会较大.机油泵不同部件的材料不同,导致机油泵从未运行状态到运行状态的过程中,因膨胀程度的不同而造成各个部件之间的配合量发生变化.

图6 从动部分的变形矢量图Fig.6 Deformation vector of driven part

在最初设计时,从动轴和从动齿轮孔径的设计尺寸分别为Φ16+0.061+0.046mm和Φ16+0.092+0.071mm.从动轴轴面和从动齿轮内孔间隙量的取值范围为0.005～0.023 mm.根据此取值范围,对从动齿轮与从动轴的初始间隙进行间隔取值及参数化设置,通过前文中热力耦合计算得到运行后间隙量的数值情况,如图7所示.从分析结果可以看出,当原始间隙为0.005～0.01 mm时,变形后间隙量已几乎消失,此时的从动齿轮与从动轴发生边界摩擦,导致接触部分迅速升温,破坏接触面,极有可能造成从动齿轮与从动轴卡死.因此,原设计的从动齿轮与从动轴的尺寸公差不合理,需改进.

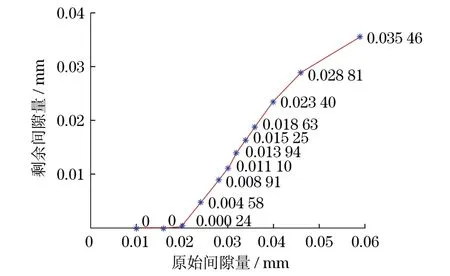
图7 运行前后从动轴轴面和从动齿轮内孔间隙量的情况Fig.7 Clearance amount between driven gear and shaft during the running state

参考滑动轴承的设计,在使用过程中为使磨损降到最低程度,同时减小对装配、制造误差的敏感性,需要油膜厚度不小于某一数值,而这一数值就是最小油膜厚度的极限值.间隙小于最小油膜厚度时会发生混合摩擦,当间隙大于最小油膜厚度时为流体摩擦[7].

最小油膜厚度极限值

式中,Rzb为轴瓦表面轮廓最大高度;Rzs为轴颈表面轮廓最大高度;φ为轴颈倾斜度;y为轴挠曲变形在轴承端面出现的挠度;B为轴颈与轴瓦的接触宽度;ae为有效波纹度[3].

根据式(3)计算得hmin=0.006 4 mm,因此,要保证油膜起到很好的润滑作用,运行后的间隙量应大于0.006 4 mm.由图7数据查询可得,原始间隙应该大于0.016 mm.

通过热力耦合分析结果,结合相关的理论计算对从动齿轮、从动轴、泵体、端盖的变形也进行了研究.从动齿轮与泵体的侧隙量主要由从动齿轮径向偏移、泵体腔壁尺寸变化、从动轴垂直度决定.从动齿轮与端盖间隙量主要由泵体油腔高度变化、从动齿轮厚度变化、垂直度对间隙决定.表2和表3即为对这些因素进行综合分析后得到的这两处间隙量在运行后的变化情况.表2和表3中的结果显示,运行后从动齿轮与泵体的侧隙量为0.014 66 mm,从动齿轮与端盖间隙量为0.049 6 mm,这样的间隙剩余量足够保证部件之间正常的润滑,不会出现卡死事故.

表2 从动齿轮与泵体侧隙量分析情况Tab.2 Analysis the clearance amount between driven gear and pump housing mm

表3 从动齿轮与端盖间隙量分析情况Tab.3 Analysis the clearance amount between driven gear and pump cover mm

2.2 原因分析

根据上述有限元分析结果可知,机油泵在极限实验情况下卡死的主要原因是从动轴与从动齿轮公差设计不当,使从动轴与从动齿轮间的间隙过小.当从动轴与从动齿轮油膜厚度过小或完全消失时,会导致配合面之间直接发生摩擦,接触面温度急剧升高,使金属产生烧结,破坏接触表面,阻碍从动齿轮运动.间隙过小时,也会使油膜温度过高,造成机油组织性能发生降化,黏度变小、抗磨性能降低,甚至碳化,进而导致接触面的磨损[8].

3 设计改进

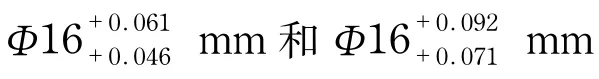
表4 优化前后的尺寸对比Tab.4 Size comparison before optimized and after optimized

由式(3)可以看出,降低Rzb和Rzs可以减小最小油膜厚度极限值,而降低Rzb和Rzs主要是通过减小从动轴和从动齿轮的表面粗糙度来实现的,这样可以使从动轴与从动齿轮在间隙量更小的情况下仍处于流体摩擦,也可以起到减少卡死故障的作用.

采用型号为MH-ZHXNCST-002的综合性能耐久测试台进行了机油泵的实验测试.对修改过尺寸公差的机油泵进行抽样实验,实验的30个样品在极限实验条件下没有出现卡死的现象.由此可以认为,对机油泵卡死故障原因的分析以及对尺寸公差的改进是合理的.

4 结 论

[1] 谭永学,王宏光,杨海玲,等.离心泵水动力噪声预测[J].上海理工大学学报,2011,33(1):89-94.

[2] 邓新源,蔡皓.转子式机油泵运动件动力学接触仿真分析[J].湖南农机,2009,36(1):20-22.

[3] 尹军,童宝宏.内燃机机油泵内部流场的可视化仿真研究[J].内燃机,2010,12(6):16-19.

[4] 王睿.机油泵内流场数值模拟分析方法研究[D].上海:上海理工大学,2013.

[5] 唐建光,朱懿渊,姚征,等.离心式风机流动特性的数值分析与改型设计[J].上海理工大学学报,2010,32(2): 136-140.

[6] 董喜俊.机油泵CFD/CAE数值模拟及试验研究[D].长沙:湖南大学,2006.

[7] 《机械设计手册》编委会.机械设计手册单行本——滑动轴承[M].北京:机械工业出版社,2007.

[8] 杨春燕,聂国权,王海花.齿轮副润滑油膜厚度的实验研究[J].石家庄铁道学院学报,2013,16(1):15-18.

(编辑:石 瑛)

Design Improvement of Sticking Phenomenon of Oil Pump Based on the Finite Element Analysis

DUBaojiang, DINGPengpeng, YU Yajun, CHEN Yuxiang
(School of Mechanical Engineering,University of Shanghai for Science and Technology,Shanghai 200093,China)

The sticking phenomenon of a kind of oil pump,encountered in its pre-production,was analyzed.By using the finite element analysis software Ansys combined with practical experiences, a more comprehensive and reasonable analysis method was proposed.The oil pump was analyzed under extreme experimental conditions.It is found that the main factor causing the oil pump’s sticking is the unreasonable dimension tolerances of the driven shaft and one of the driven gears. According to that appropriate measures were adopted for design improvement.The improvement scheme was validated through experiments,and the rationality of the analysis was finally proved.

oil pump;sticking;Ansys software;fault analysis;design improvement

TH 122

A

1007-6735(2015)03-0269-05

10.13255/j.cnki.jusst.2015.03.012

2014-02-21

杜宝江(1962-),男,副教授.研究方向:虚拟制造.E-mail:fly2happy@163.com