双参数指数分布型元件冷储备系统可靠性的广义近似置信限

崔媛媛，郑海鹰，李晓飞

(温州大学数学与信息科学学院，浙江温州 325035)

双参数指数分布型元件冷储备系统可靠性的广义近似置信限

崔媛媛，郑海鹰†，李晓飞

(温州大学数学与信息科学学院，浙江温州 325035)

利用广义近似置信限的方法和E-Bayes方法对定时截尾试验数据下冷储备系统的可靠性指标进行了估计，得到系统可靠性的广义近似置信限和E-Bayes近似置信限．蒙特卡罗方法模拟结果表明：小样本下，E-Bayes方法比广义近似置信限具有显著优势；大样本下，广义近似置信限比E-Bayes近似置信限有较大优势．

双参数指数分布；冷储备系统；E-Bayes方法；广义近似置信限

系统可靠性指标的近似置信限研究是可靠性工程理论研究的重要组成部分．双参数指数分布是一种应用很广的寿命分布，很多产品的寿命都可以用它很好地刻画．吴和成[1]、严惠云等[2]利用经验贝叶斯的方法求出了双参数指数分布下冷储备系统的近似置信限，吴和成[1]对开关不可靠的冷储备系统的近似置信下限进行了分析．但是由于讨厌参数v的存在，我们很难精确计算其置信限．因此，本文考虑了由n个元件和一个切换开关组成的冷储备系统，试验终止当且仅当切换开关失效或开关不失效直到所有备用部件用完，且n个元件的寿命都相互独立，服从双参数指数分布；然后利用Werrahandi推广的置信限概念[3]建立系统可靠性指标的广义近似置信限和系统可靠度的E-Bayes近似置信下限，并将系统可靠度的广义置信下限与E-Bayes近似置信下限进行比较，得出在样本数据不同时，广义置信限与E-Bayes置信限的优劣．

1 模型与基本假定

假设1 冷储备系统由n个元件和一个切换开关组成，开始工作时有一个元件工作，n-1个元件做冷储备．

假设2 当工作元件失效时，开关切换到冷储备元件，出现以下情况之一时系统失效：

（1）使用切换开关时开关失效；

（2）开关正常运行，直到n-1个备用部件用完时开关失效．

假设3 n个元件的寿命服从相互独立的参数为u, v的双参数指数分布，其概率密度为：

其部件可靠性函数为：

当参数v给定时，参数u的先验分布为：

假设4 切换开关寿命为0- 1型，每次使用开关成功的概率为p，元件的寿命与开关的好坏也相互独立．

为求系统可靠度，引入随机变量s，令：

则：

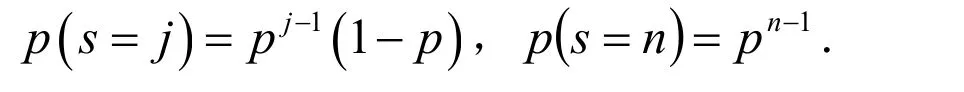
2 冷储备系统的近似置信下限

假设对部件都进行定数截尾试验，依据获得的定数截尾数据建立其R(t )的近似置信下限．

设x1,x2,…xn为来自样本的元件，对样本进行定数截尾试验，设元件的失效数目为k，x(1)＜x(2)＜…＜x(k )表示x1,x2,…xn中最小的k个寿命观测值．

用随机变量Y来表示冷储备系统的寿命，有：

由于x1,x2,…xn与开关好坏相互独立，因此它们与随机变量s相互独立，故系统可靠度为：

2.1 系统可靠性的广义置信下限

则得系统可靠度的广义置信下限为（4）．

2.2 系统可靠性指标的E-Bayes置信下限

3 数值模拟

3.1 可靠度置信限比较

（1）考虑由5个部件3个储备部件组成的冷储备系统，随机产生失效数目r，失效时间T，定数截尾实验数据x(1)＜x(2)＜…＜x(k )，及定时截尾数据t1＜t2＜…＜tk，服从倒伽马分布的参数u1,u2，及参数v的定值v1,v2．分别以u1,v1为真值，u2,v2为计算给出的估计值；

（2）将u1,v1,u2,v2分别代入r(t )得到参数u的置信下限，再将u1,v1,u2,v2代入冷储备系统公式得到系统可靠度的置信下限；

（3）将u1,v1代入r(t )，得到部件失效率r(t )的值，将部件失效率r(t )，失效数目r，以及既定时间T分别代入R(t )得到冷储备系统可靠性近似置信限的E-Bayes近似置信，广义近似置信限与E-bayes置信限．

计算结果见表1．

表1 随机模拟结果

由表1可知：当样本数据较少的情况，E-Bayes近似置信限与广义近似置信限具有显著差异，且由模拟结果可知可靠性指标的E-Bayes置信限与真值更为接近，且E-Bayes比广义近似置信限更加精确．当样本数据较大时，广义近似置信限比E-Bayes近似置信限与真值更为接近，且可靠性较高．

3.2 置信限精度的优劣比较

（1）给定u,v的值u*,v*，利用随机模拟产生一组u,v值，选取其中一个记为真值，失效时间T，定数截尾实验数据x(1)＜x(2)＜…＜x(k )，及定时截尾数据t1＜t2＜…＜tk，服从倒伽马分布的参数u1,u2，利用得到的的u,v值分别代入可靠性公式式得到．

（2）数截尾实验数据x(1)＜x(2)＜…＜x(k )，及定时截尾数据t1＜t2＜…＜tk，服从倒伽马分布的参数u1,u2带入公式分别得到uG、uE、RG和RB．

（3）重复步骤（1），（2）N次，分别得到N组数据，分别考虑E-Bayes近似置信限与广义近似置信限覆盖u*,的比例C0．计算结果见表2．

表2 精度优劣比较模拟结果

由表2可知：样本数据较多的情况下，广义近似置信限比E-Bayes近似置信限具有更好的精度；而在小样本数据情况下，E-Bayes近似置信限估计具有的优势较为显著．

4 结 论

本文利用Werrahandi推广的置信限概念[3]，建立起系统可靠性指标的广义近似置信限，同时也建立了系统可靠度的E-Bayes近似置信下限．通过蒙特卡罗方法进行模拟，将系统可靠度的广义置信下限与E-Bayes近似置信下限进行了比较，得出在样本数据不同时，广义置信限与E-Bayes置信限的优劣．

[1] 吴和成. 转换开关不完全可靠的冷贮备系统可靠性的置信限[J]. 连云港化工学报, 1995, (Z1): 1-5.

[2] 严惠云, 师义民. 并联系统可靠性指标的多层Bayes近似置信限[J]. 西南民族大学, 2007, 24(1): 39-41.

[3] 师义民, 寇开昌, 周巧娟. 定数双截尾样本下K/N(G)系统可靠性指标的经验贝叶斯估计[J]. 数学的实践与认识, 2007, 37(1): 84-88.

[4] 茆诗松, 吕晓玲. 数理统计学[M]. 北京: 中国人民大学出版社, 2011: 152-155.

[5] 武东, 汤银才. 指数分布逐次定数截尾试验的多层贝叶斯估计[J]. 上海第二工业大学学报, 2011, 28(2): 114-116.

[6] 刘永峰, 郑海鹰. 无失效数据失效率的综合E-Bayes估计[J]. 温州大学学报: 自然科学版, 2011, 32(10): 7-13.

[7] Shi Y M, Shi X L, XU Y. Approximate confidence limits of the reliability performances for a cold standby series system [J]. Appl math & computing, 2005, 28(2): 439-445.

[8] 峁诗松. 贝叶斯统计[M]. 北京: 中国统计出版社, 1999: 13-20.

[9] 曹晋华. 可靠性数学引论[M]. 北京: 高等教育出版社, 2002: 57-66.

[10] 赵宇, 杨军, 马小兵. 可靠性数据分析教程[M]. 北京: 北京航空航天大学出版社, 2003: 122-131.

On the Reliability of Two-parameter Exponential Distribution for Cold Standby System and Its Generalized Approximate Confidence Limits

CUI Yuanyuan, ZHENG Haiying, LI Xiaofei
(College of Mathematics and Information Science, Wenzhou University, Wenzhou, China 325035)

In this paper, the reliability index of cold standby system under the timing truncation experimental data is evaluated by means of generalized approximate confidence limit and E-Bayes methods. Therefore, the generalized method of approximate confidence limits and the E-Bayes approximate confidence limit of the system reliability are obtained. The simulated result of Monte-carlo method indicates that E-Bayes method under small samples has significant advantages over the generalized approximate confidence limit, while under large samples the result is on the contrary.

Two-parameter Exponential Distribution; Cold Standby System; E-Bayes Method; Generalized Approximate Confidence Limits

O213

A

1674-3563(2015)03-0001-08

10.3875/j.issn.1674-3563.2015.03.001 本文的PDF文件可以从xuebao.wzu.edu.cn获得

(编辑：封毅)

2014-08-15

崔媛媛(1988- )，女，山西长治人，硕士研究生，研究方向：应用统计．† 通讯作者，wzzhying@163.com