基于模糊C均值的水平集活动轮廓模型

吕红力

(温州大学数学与信息科学学院，浙江温州 325035)

基于模糊C均值的水平集活动轮廓模型

吕红力

(温州大学数学与信息科学学院，浙江温州 325035)

针对SPF模型的水平集函数初始化方式不灵活、容易发生边界泄漏的问题，提出一个新的基于模糊C均值的水平集活动轮廓模型．首先，用图像灰度值与两个模糊聚类中心的平均灰度值的差构造一个模糊符号压力函数，并证明它能够调节目标区域内外的压力符号，用模糊符号压力函数取代SPF模型中的SPF函数；其次，使用正则化的Dirac函数δ( )φ取代|▽φ|；最后，使用高斯滤波平滑水平集函数．实验表明，提出的方法精确有效．

SPF模型；模糊符号压力函数；活动轮廓模型；图像分割；模糊C均值

图像分割在图像处理和图像分析中具有非常重要的地位，在计算机视觉、物体追踪、医学图像分割等方面有着广泛的应用[1]．目前关于图像分割的方法已有很多，例如，直方图阈值、区域增长、聚类、活动轮廓模型等方法，但是，由于图像变化多样，种类繁多，图像分割依然是一个具有挑战性的研究课题．模糊C均值（FCM）[2]是图像分割的一种基本方法，它属于软分割法，相对于硬分割方法，FCM能保留更多的图像信息，能更加真实地反映事物的模糊性与不确定性．活动轮廓模型大致可分为两类，基于边缘的活动轮廓模型[3-5]和基于区域的活动轮廓模型[6-8]．张开华等人结合基于边缘的GAC模型[4]和基于区域的CV模型[6]提出了SPF模型[9]，该模型实现简单，抗噪性能较优，但也具有如下缺点：1）随着迭代次数的增加，容易产生边缘泄漏，甚至演化曲线消失不见；2）水平集函数不可以采取更自由的初始化方式，例如，初始化为一个常值函数或者一个点；3）水平集函数初始化的位置不自由，不同的初始化位置可能得到不同的分割结果．

鉴于以上分析，本文提出一个新的基于区域的水平集活动轮廓模型，利用轮廓内外的模糊统计信息构造一个基于区域的新符号压力函数，它在分割目标的内部和外部具有符号相反的性质，能够自动地控制轮廓线的收缩或者扩张．为了保持水平集函数的光滑性和演化的稳定性，采用高斯滤波正则化方法来平滑水平集函数．本文所提出的模型可以处理光滑或者不连续边缘，具有实现简单、全局分、计算量小的优点，水平集函数的初始方式更加简单自由，初始化的位置可以设置在图像中的任何一个地方．

1 背 景

1.1 SPF模型

文献[9]提出一个结合了GAC模型与CV模型的优点的基于区域的活动轮廓模型（SPF模型），构造一个符号压力函数并取代GAC模型中的边缘停止函数．水平集函数的演化方程为：

其中，α为固定参数，spf( I( x))是利用区域统计信息定义的符号压力函数，定义如下：

式中，c1, c2来自于CV模型，分别表示曲线C内部和外部的图像灰度均值，定义如下：

1.2 FCM算法

设图像I包含N个像素点，假设图像被分为两类，每个点x∈I都对应一个灰度值I( x)，隶属度u( x)，在FCM算法中，分割图像可以通过最小化如下能量函数：

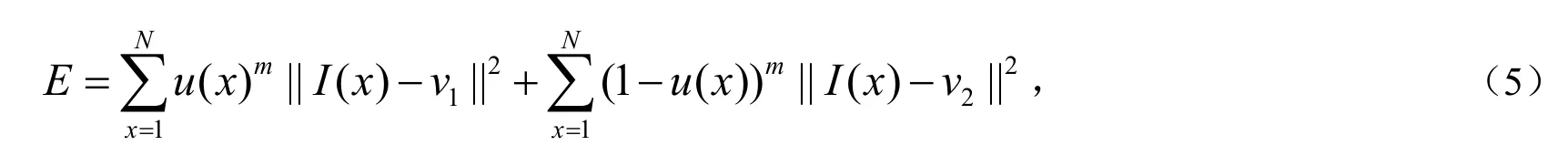
其中，m为隶属指数．根据Lagrange数乘法，可得到使能量函数（5）取得极小值的必要条件为：

把（6）式和（7）式改写为连续形式如下：

模糊C均值算法在分割图像时，具有实现简单，无监督等特点，得到了广泛的研究和应用．

2 基于模糊C均值的水平集模型

2.1 SPF函数构造

SPF函数[10]能够自动调节目标区域内外的符号，使演化曲线能够自动收缩或者扩张．受SPF模型的启发，定义一个基于模糊统计信息的SPF函数如下：

其中v1和v2来自于式（9）式（10）式．为了方便讨论所定义的符号压力函数的性质，假设二值图像：

其中，a和b是两个互不相等的非负常数，ω和Ωω分别表示图像的目标区域和图像的背景区域．本文推导出如下性质（详细证明见附录）：

容易得到-1≤spf( I )≤1，并且在目标区域内外异号，可以实现演化曲线的自动收缩或者扩张，因此初始化轮廓可以设置在图像的任意位置．

2.2 本文模型

用式（11）中的fspf( I( x))取代式（1）的spf( I( x))，得到：

为了提高防边缘泄漏的能力，用正则化的Dirac函数δε( φ)取代式（13）中的|▽φ|，模型进一步改写为：

1）新模型中的v1和v2与SPF模型中的c1和c2有本质上的不同，新模型是基于模糊集合理论，属于软分割的范畴，而SPF模型是基于经典集合，属于硬分割，新模型能保留更多的图像信息；

2）本文模型用δε( φ)取代了|▽φ|，提高了抗边缘泄漏能力；

3）新模型对初始化轮廓不敏感，可以设置到图像中的任意一个位置，可以灵活地选择初始化方式．

2.3 水平集函数的初始化方式

初始化曲线一般可以选择为图像域中的一条封闭的曲线，这样可以使活动轮廓能更好地处理内部区域，如，设置初始化曲线为符号距离函数．下面给出三种其它初始化方式：

1）初始曲线φ0(x)可以定义为一条封闭的曲线，例如圆或者矩形，定义可以为如下的二值函数：

其中，常数ρ≠0；

3）初始化为一个点．

2.4 算法步骤

主要的算法流程如下：

1）初始化水平集函数0φ；

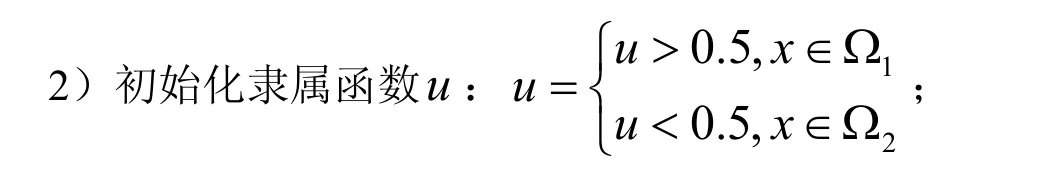
3）根据（9）式和（10）式分别计算v1和v2；

4）根据（8）式更新隶属函数；

5）根据（15）式演化水平集函数；

6）用高斯滤波平滑水平集函数，φ=Gσ*φ，其中，Gσ是标准差为σ的高斯核函数；

7）检查水平集函数是否收敛，如果收敛，停止，否则，返回第3步．

3 实验结果

本文实验采用Matlab编程，实验是在4G内存的PC机上、Windows7、Matlab 2014a环境下完成的．本文主要从三个方面与SPF模型进行比较：1）水平函数初始化方式的多样性；2）水平函数初始化位置的任意性；3）抗边缘泄漏能力．实验中，参照文献[9]，选取参数为：ρ=1，ε=1.0，σ=1.0，K=5，α=25，时间步长Δt=1．

实验1 水平函数初始化方式的多样性

图1给出的是一副人工合成的图像分割结果，图像的左侧边缘有轻微的灰度不均匀，第一行依次采用了2.3中三种不同的初始化方式，第二行是本文模型的分割结果，第三行是SPF模型的分割结果．可以看出本文模型在三种不同的初始化方式下都取得了很好的分割效果，而SPF模型只有在第一种初始化方式下才能正确分割．说明本文模型的水平集函数初始化方式更自由，而且能处理轻度灰度不均的图像．

图1 本文模型与SPF模型的分割结果 (不同的初始化方式)

实验2 水平集函数初始化位置的任意性

图2给出了一副灰度轻微不均的书法汉字图像分割结果．第一列是初始化位置，第二列是本文模型的分割结果，第三列是SPF模型分割结果．从分割结果可以看出，SPF模型在情况b和c下才取得了正确分割，而本文模型在四种情况下都取得了正确分割．说明本文的模型对水平集函数的初始化位置不敏感．

实验3 抗边缘泄漏能力

图3是一副书法图像在不同的迭代次数下两种模型的分割结果．图3中图b是本文模型迭代3次的分割结果，耗时0.013 s，图d是SPF模型迭代50次的分割结果，耗时0.483 s，可看出本文模型耗时少，收敛速度快．本文模型迭代2 500次（图c）没有出现边缘泄漏，而SPF模型迭代170次（图f）轮廓线就部分消失，190次（图h）完全消失，说明本文模型抗边缘泄漏能力强．

图2 本文模型与SPF模型的分割结果 (不同的初始化位置)

实验4 医学图像分割

图4是一副手骨X光图像的分割结果．手骨X光图像中呈现出灰度分布不均匀的情况，而且两根手指中有六个不同的骨节，其中左侧骨尖处基本与肌肉的图像融合在了一起．图a是水平集初始化的位置，图b是本文模型的分割结果，图c是SPF模型的分割结果．从分割结果可以看出，本文模型可以正确地分割六段骨节，在指尖处也得到了正确的分割，而SPF模型没有分割出指尖处的两段骨节，且在右侧中间骨节的上端没有正确的定位骨节边缘．实验4的结果表明本文模型在分割灰度不均和多目标图像上比SPF模型具有优势．

图3 本文模型与SPF模型在不同的迭代次数下的分割结果

图4 手骨X光图像的分割结果

4 结束语

本文提出一种新的基于模糊C均值的活动轮廓模型，与SPF模型相比，该模型的水平集函数初始化方式灵活，初始化位置自由，无边缘泄漏问题，计算效率高，收敛速度快，实现简单，可以得到全局最优分割，这些在对合成图像、真实图像的分割实验中已经得到了验证，同时实验结果也显示出本文模型能分割轻度不均图像．

[1] Shyu K K, Pham V T, Lee P L. Global and local fuzzy energy-based active contours for image segmentation [J]. Nonlinear Dynamics, 2012, 67: 1559-1578.

[2] Gong M G, Yan L, Jiao S, et al. Fuzzy C-means clustering with local information and kernel metric for image segmentation [J]. IEEE Transaction on Image Processing, 2013, 22(2): 573-584.

[3] Li C M, Xu C Y, Gui C F, et al. Distance regularized level set evolution and its application to image segmentation [J]. IEEE Transaction on Image Processing, 2010, 19(12): 154-164.

[4] Caselles V, Kimmel R, Sapiro G. Geodesic active contours [J]. International Journal of Computer Vision, 1997, 22(1): 61-79.

[5] Kass M, Witkin A, Terzopoulos D. Snakes:active contour models [J]. International Journal of Computer Vision, 1988, 1(4): 321-331.

[6] Chan T F, Vese L A. Active contours without edges [J]. IEEE Transaction on Image Processing, 2001, 10(2): 266-277.

[7] Paragios N, Deriche R. Geodesic active regions and level set methods for supervised texture segmentation [J]. International Journal of Computer Vision, 2002, 1(46): 223-247.

[8] Li C M, Kao C Y, Gore J, et al. Minimization of region-scalable fitting energy for image segmentation [J]. IEEE Transactions on Image Processing, 2008,17(10): 1940-1949．

[9] Zhang K H, Song H H, Zhang L. Active contours with selective local or global segmentation: a new formulation and level set method [J]. Journal of Image and Vision Computing, 2010, 28(4): 668-676.

[10] Xu C Y, Jr A Y, Prince J L. On the relationship between parametric and geometric active contours [EB/OL]. [2014-05-08]. http://wenku.baidu.com/link?url=quQyiWoJ9Vcj1-2YyFlyY7ROtBG0UTrnS8M_H3mz4X_JGdNQjo vuDsYwoizeLJ2VW8evmn9coVxyHs303b0ROEO3xk8S8IWNDa_UWjY6whK.

附录：

证明：在ω内，有：

在Ωω内，有：

又有如下事实：

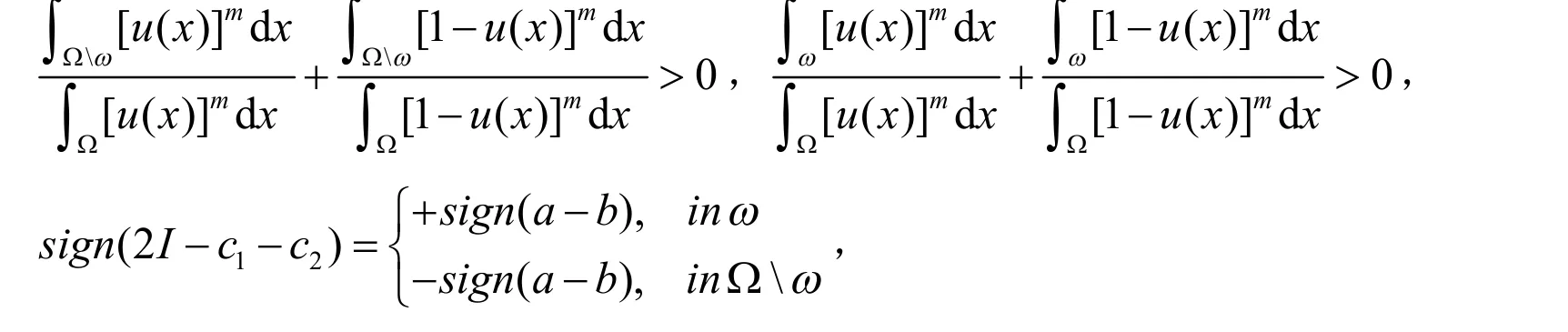
因此有：

(编辑：王一芳)

Level Set Active Contour Model Based on Fuzzy C-means

LV Hongli
(School of Mathematics and Information Science, Wenzhou University, Wenzhou, China 325035)

In this paper a new level set active contour model based on fuzzy C-means is raised in allusion to the problem of SPF model that the way of level set initialization is inflexible and boundary is prone to leak. The experiment is made as follows: Firstly, a fuzzy signed pressure force (FSPF) function is constructed by the difference between the image gray value and the average gray value of the two fuzzy clustering centers, and shown to modulate the signs of pressure forces inside and outside the region of object. The fuzzy signed pressure force function is substituted for the SPF function of SPF model. Secondly,|▽φ|is replaced by regularization Dirac functionδ( )φ. Finally, level set function is smoothed by Gaussian filter. Experimental results indicate that the proposed method is accurate and effective.

SPF Model; Fuzzy Sign Pressure Function; Active Contour Model; Image Segmentation; Fuzzy C-means

TP319.41

A

1674-3563(2015)03-0025-09

10.3875/j.issn.1674-3563.2015.03.004 本文的PDF文件可以从xuebao.wzu.edu.cn获得

2014-06-23

吕红力(1982- )，男，河南商丘人，硕士研究生，研究方向：数字图像处理