双车动力学模型的数值模拟改进研究
2015-06-23常丑娥辛瑞峰
常丑娥,辛瑞峰
(1.忻州师范学院数学系,山西忻州 034000;2.原平职业高级中学,山西原平 034100)
双车动力学模型的数值模拟改进研究
常丑娥,辛瑞峰
(1.忻州师范学院数学系,山西忻州 034000;2.原平职业高级中学,山西原平 034100)
选取双车动力学模型描述交通流,用一阶迎风格式和MHM格式寻求了相应的数值解,然后用改进的高阶MHCM差分格式得出相应的新的数值解,最后对不同的数值解进行分析比较.数值模拟结果表明,高阶修正MHCM格式耗散小、精度高,而且能更有效的描述交通流的冲击波和疏散波,效果较好.
交通流;MHCM格式;双车动力学模型
我国许多中小城市由于车道窄、交通拥挤等原因,交通阻塞现象频发.针对这种车辆单车道行驶且单车道上无超车行为的交通现象,彭光含等学者[1]提出了适用于上述条件的模型,由于该模型考虑到了邻近前车与次邻近前车的信息,所以称为双车动力学模型.该模型不仅可以体现出行驶车辆受前方车辆影响,也就是扰动只能向后传播,同时也体现出不同类型车流在整个路段的行驶情况,可以预先获得前面车辆状态信息,从而使跟驰车辆的驾驶员提前加速或减速,避免驾驶员频繁地改变速度[2].对双车动力学模型数值模拟改进研究能更好地改善城市交通拥挤、交通堵塞等现象,从而更好地解决城市交通问题,提高交通流的稳定性.
现有的交通流确定性模型有宏观模型和微观模型之分[3-4].宏观模型有LW模型[5]、LWR模型[6]、Payne模型[7]、Phillips模型[8]、吴正模型[9]、Daganzo模型[10]、Zhang模型[11]等,主要采用流体动力学理论,特点不仅是不存在唯一的速度-密度关系,而且考虑了时间和空间的因素.微观模型有经典车辆跟驰模型[12],OVM模型[13]、GFM模型[14]、FVD模型[15]等,主要采用车辆跟驰理论.近年来,一些学者利用宏观模型和微观模型的特点将两者相结合,提出新型的模型,如姜锐-吴凊松模型[16],双车动力学模型[1]等.我国城市交通以低速混合交通为主[17],道路中普遍存在机动车和非机动车以及性能相差悬殊的各种车辆混行的交通现象[18].双车动力学模型正好能体现出整个路段中各种大小车型的比例情况,且考虑了次邻近前车的信息以及次邻近前车车辆对交通流的影响.
本文针对双车动力学模型的方程组为双曲型方程组和原有的一阶差分格式、MHM格式存在的问题,重新构造了高阶修正MHCM格式,该格式耗散小,精度高,能更有效的描述交通流的疏散、聚集情况,比如遇到交通信号灯、交通事故堵塞疏散等情形.
1 模型及描述
双车动力学模型为:

它的适用条件是:1)车辆无换道行为,可理解为单车道行驶;2)在单车道上无超车行为.其中ρ是密度,v是速度,Ve是平衡速度,c0是小扰动传播速度,由所在路段的实测数据具体路段具体给定,T是松弛时间,n为大型车所占整个车流的百分比.
该模型考虑了次邻近前车的信息以及次邻近前车车辆对交通流的影响,可以预先获得前面车辆状态信息,可以使跟驰车辆的驾驶员提前加速或减速,避免驾驶员频繁地改变速度,从而增强车流稳定性.该模型中没有大于宏观车流运动速度的特征速度[19],符合实际交通流情况[20],它不仅能够模拟交通流的堵塞、疏导等实际交通现象,而且也考虑了整个路段中车型大小的比例情况.
2 方法改进
2.1 模型的原始差分格式
双车动力学模型为双曲型方程组,模型的原始差分格式是文献[16]中的格式.
连续方程采用格式:

2.2 模型的MHM格式
文献[21]中的高阶差分格式为MHM格式:
连续方程采用:

动力学方程采用:

2.3 高阶修正的MHCM格式
根据地点车辆与邻近车辆、次邻近车辆均有密切关系,对连续方程的差分格式进行修正.


对该模型的动力学方程的差分格式进行高阶修正.


其中该格式的通量为MUSCL-Hancock Centred Method通量[22],简称为MHCM通量,即MHCMf,

3 数值模拟及分析比较
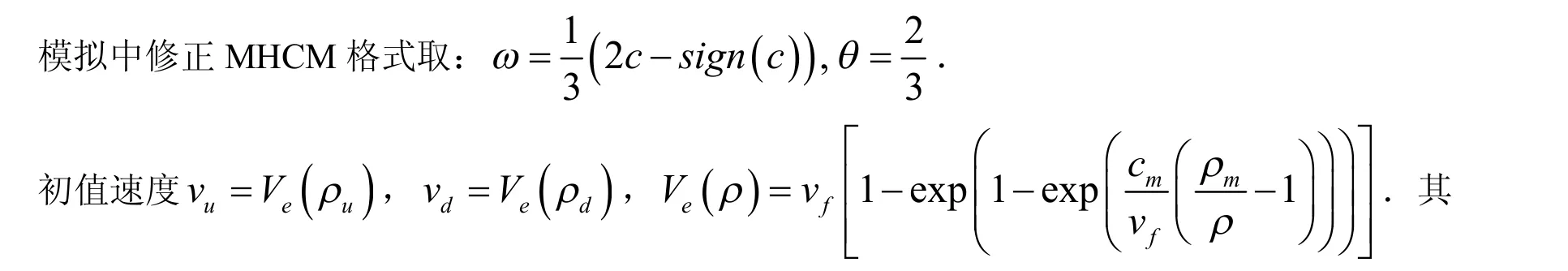
中vu和vd分别为上、下游车流速度,uρ和dρ分别为上、下游车流密度,cm是堵塞的扰动传播速度,vf是自由流速度,mρ是堵塞密度.


图1 n=0, t=120 s时的交通流密度

图2 n=0.5, t=120 s时的交通流密度
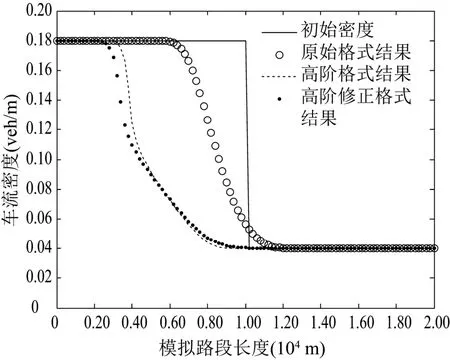
图3 n=1, t=90 s时的交通流密度
用双车动力学模型模拟交通流密度.数值采用ρu=0.18,ρd=0.04.利用方法改进中的2.1,2.2,2.3三种差分格式分别进行数值模拟,原始格式为文献[16]中的一阶有限差分格式,高阶格式为文献[21]中的MHM格式,高阶修正格式为论文中提出的修正MHCM格式.n为大型车所占整个模拟路段上车流的比例,t为进行数值模拟的时间.
例1 用双车动力学模型模拟交通流的消散波,见图1-图3.
图1-图3表示不同时段不同车型比例条件下的交通流密度.图1表示在整个路段全为小型车流的情况下,交通疏散120 s时的交通密度;图2表示在整个路段大型车与小型车数量相同的情况下,交通疏散120 s时的交通密度;图3表示在整个路段全为大型车流的情况下,交通疏散90 s时的交通密度.
从图中观察到在该Riemann初始值条件下交通流产生稀疏波.三幅图都可以得出相同的结论,在相同条件下,不同差分格式均可将其消散,然而消散程度不同.高阶修正MHCM格式的疏导效果较好,更利于交通运行.说明利用高阶修正MHCM格式,消散快,使交通顺畅,易于疏导.
例2 用双车动力学模型模拟交通流的冲击波,见图4-图6.
图4-图6表示不同时段不同车型比例条件下的交通流密度情况.图4中表示在整个路段全为小型车流的情况下,交通流聚集120 s时的交通密度以及部分区域的密度特写;图5表示在整个路段大型车与小型车数量相同的情况下,交通流聚集120 s时的交通密度及部分特写;图6表示在整个路段全为大型车流的情况下,交通流聚集120 s时的交通密度及部分区域密度特写.部分区域特写能更好的体现交通密度情况.
图4-图6描述了交通流聚集(冲击波)的处理情况.经过分析比较得出,在同一时间段相同车型比例的条件下,采用三种差分格式进行数值模拟的计算结果不同,显然利用高阶修正MHCM格式进行模拟能更好地描述交通流的运动状态,体现出交通流密度的运动特性,清楚地看到双车信息对交通流增强了向后传播的惯性,增强了交通流的稳定性.

图4 n=0, t=120 s时的交通流密度

图5 n=0.5, t=120 s时的交通流密度

图6 n=1, t=120 s时的交通流密度
4 结 论
高阶修正MHCM格式不需要解黎曼解算器、不需要在特征线方向投影、避免了特征线的分解,耗散小、精度高.通过数值模拟说明利用高阶修正MHCM格式可更好地解决交通事故波、交通红绿灯、交通堵塞等现象中的冲击波和稀疏波,不仅使交通波的传播速度较快,车流疏散程度较好,而且使交通流增强了向后传播的惯性,增强了交通流的稳定性,能更有效地应用于实际交通流中.此研究有助于进一步理解司机驾车行为和交通流的非线性动力学特性,有利于交通管理与控制水平的提高.
[1] 彭光含, 孙棣华, 解佳, 等. 交通流双车动力学模型与数值仿真[J]. 系统仿真学报, 2008, 20(2): 272-276.
[2] 彭光含, 孙棣华, 何恒攀. 交通流双车跟驰模型与数值仿真[J]. 物理学报, 2008, 57(12): 7541-7546.
[3] 王亦兵, 韩曾晋, 史其信. 高速公路交通流建模[J]. 系统工程学报, 1998, 13(2): 83-89.
[4] 宫晓燕, 汤淑明, 王知学, 等. 高速公路交通流建模综述[J]. 交通运输工程学报, 2002, 2(1): 74-79.
[5] Lighthill M J, Whitham G B. On kinematic maves: II. a theory of traffic flow on long crowed roads [J]. Proceedings Royal Society London Series A, 1955, 229(1178): 317-345.
[6] Richards P I. Shock waves on the highway [J]. Operation Research, 1956, 4: 42-51.
[7] Payne H J. Models of freeway traffic and control [J]. Mathematical Methods of Public Systems, 1971, 1(1): 51-61.
[8] Phillips W F. A new continuum traffic model obtained from kinetic theory [J]. The IEEE Transaction on Automatic Control, 1978, 23: 1032-1036.
[9] 吴正. 交通流的动力学模拟与测量方法[J]. 复旦学报: 自然科学版, 1991, 30(1): 111-117.
[10] Daganzo C F. The cell transimission model: a dynamic representation of highway traffic consistent with the hydrodynamic theory [J]. Transportation Research Part B: Methodological, 1994, 28(4): 269-287.
[11] 唐铁桥, 黄海军. 两车道交通流模型与数值计算[J]. 科学通报, 2004, 49(19): 1937-1943.
[12] Gazis D C, Herman R, Rothery W. Nonlinear follow-the-leader models of traffic flow [J]. Operation Research, 1961, 9: 545-567.
[13] Bando M, Hasebe K, Nakayama A, et al. Dynamical model of traffic congestion and numerical simulation [J]. Physical Review E, 1995, 51: 1035-1042.
[14] Helbing D, Tilch B. Generalized force model of traffic dynamics [J]. Physical Review E, 1998, 58: 133-138.
[15] Jiang R, Wu Q S, Zhu Z J. Full velocity difference model for a car-following theory [J]. Physical Review E, 2001, 64(1): 017101(1)-017101(4).
[16] 姜锐, 吴清松, 朱祚金. 一种新的交通流动力学模型[J]. 科学通报, 2000, 45(17): 1895-1899.
[17] 孟维伟, 曹从咏, 陈新. 改进时空步长一维交通流的数值模拟[J]. 交通与计算机, 2006, 24(3): 14-17.
[18] 谢军, 严宝杰, 张生瑞. 城市环形交叉口通行能力理论模型[J]. 长安大学学报: 自然科学版, 2007, 27(4): 75-78.
[19] 马标, 彭建文. 交通流的各向异性模型研究[J]. 中国水运, 2007, 5(7): 139-140.
[20] Daganzo C F. Requiem for second-order fluid approximations of traffic flow [J]. Transportation Research B, 1995, 29: 77-286.
[21] 常丑娥. 双车动力学交通流模型的研究与数值模拟[D]. 陕西: 长安大学, 2010: 11-13.
[22] Toro E F. Riemann solvers and numerical methods for fluid dynamics [M]. New York: Springer-Verlag Berlin Heidelberg, 1997: 379-477.
The Improvement Research of Numerical Simulation for Two-car Dynamical Model
CHANG Chou’e, XIN Ruifeng
(1. Department of Mathematics, Xinzhou Normal College, Xinzhou, China 034000;2. Yuanping Vocational High School, Yuanping, China 034100)
This paper picks out the two-car dynamical model to describe the traffic flow. Firstly, using the first order upwind scheme and the MHM scheme quests the relevant numerial solution. Then, using the modified high order MHCM scheme obtains the new numerical solution. Finally, the different numerical solutions are analyzed and compared one by one. The simulated result of numerical value indicates that the modified MHCM scheme is better than the old scheme for its small dissipation, high precision and more effective to describe the shock wave and evacuation wave of traffic flow.
Traffic Flow; MHCM Scheme; Two-car Dynamical Model
U491.1
A
1674-3563(2015)03-0009-08
10.3875/j.issn.1674-3563.2015.03.002 本文的PDF文件可以从xuebao.wzu.edu.cn获得
(编辑:封毅)
2014-08-28
常丑娥(1984- ),女,山西忻州人,助教,硕士,研究方向:科学与工程问题的高性能计算技术
