一种基于SIFI的DWT域抗几何攻击水印算法

吕建平， 彭 述

(西安邮电大学 计算机学院， 陕西 西安 710121)

一种基于SIFI的DWT域抗几何攻击水印算法

吕建平， 彭 述

(西安邮电大学 计算机学院， 陕西 西安 710121)

针对基于小波变换的图像水印算法抗几何攻击问题，提出一种改进的水印算法。该算法先对图像进行三级离散小波变换，利用奇偶量化规则将水印嵌入到低频系数的最大奇异值上。通过尺度不变特征变换特征点估算出几何失真参数，再校正图像并提取水印，达到抵抗几何攻击的目的。实验结果表明，该算法不仅能抵抗JPEG压缩、噪声、滤波等常规信号处理攻击，也能较好地抵抗旋转、缩放、平移等几何攻击。

尺度不变特征变换；离散小波变换；奇偶量化规则；最大奇异值；几何攻击

数字水印技术利用数字作品的冗余性和自相关性，将标志数字作品版权的信息如随机序列，二值图像和灰度图像嵌入到音频、图像、视频等数字作品中，可以起到版权保护和内容认证的目的[1]。当版权被侵犯时，可以提取隐藏在数字作品中的版权信息，并以此作为起诉侵权的证据。随着互联网时代的到来，数字水印技术已成为数字作品版权保护的一种重要技术手段。

目前，基于离散小波变换的数字水印技术已经成为数字水印领域的一个研究热点。很多学者都提出了在小波域嵌入水印信息的算法，它们具有很强的鲁棒性[2-4],但小波变换不具备几何变换不变性，很多基于小波变换的水印算法在抗几何攻击方面都不太理想。而图像的特征点则具有协变于几何变换的能力[5]，可将其用在抗几何攻击水印算法中，如文献[1]使用Harris-Laplace特征点对图像进行校正，取得效果比较好，但实时性较差，文献[5]则以多尺度Harris特征点为中心，首先划分若干特征区域，然后在特征区域中嵌入水印信息，效果也比较好，但水印的嵌入量小且实时性也比较差。目前主要的特征点算子[6]有Harris、Harris-Laplace和尺度不变特征变换(Scale Invariant Feature Transform, SIFT)。SIFT作为一种最新的特征点算子，不仅具有旋转，缩放，平移不变性，也能基本满足实时性要求[7-8]。因此本文在将水印嵌入到图像小波变换域的基础上，提出一种基于SIFT特征点的水印算法，利用SIFT特征点的几何不变性校正图像的几何失真，使水印具有一定的抗几何攻击能力，并用实验来验证算法的抗几何攻击能力。

1 相关理论

1.1 SIFI特征点的检测与匹配

1.1.1 特征点的检测

SIFT特征点提取是在高斯差分(Difference Of Gaussian， DOG)尺度空间完成。一幅图像的尺度空间可用L(x,y,δ)表示，其定义为图像I(x,y)和一个尺度可变的二维高斯函数做卷积运算[9]

其中(x,y)是空间像素坐标；δ是尺度坐标，其大小决定图像平滑程度。G(x,y,δ)被称为高斯核函数，它被认为是唯一可以产生多尺度空间的核。

提取SIFT特征点时，首先用不同尺度的高斯核函数和原始图像做卷积运算，得到一系列尺度空间，然后取相邻两者之差，即可得到DOG尺度空间，如图1所示。

图1 DOG尺度空间

在求取图像的DOG尺度空间后，将DOG尺度空间中的每个点与它同尺度的8个相邻点和上下相邻尺度的18个相邻点作比较，若是极值点，则将此点作为候选的特征点。最后通过拟合三维二次函数精确特征点的位置和尺度，同时去掉低对比度和不稳定的边缘特征点即得到所需的特征点集。在求得特征点后，把以特征点为中心的16×16的矩形窗口分成16个4×4大小的子块，对每个子块统计8个方向的梯度直方图，共有16×8=128个方向作为该特征点的特征向量。

1.1.2 特征点的匹配和图像的校正

图像校正时需要对失真前后图像的两个SIFT特征点进行匹配，此时只需计算两特征点特征向量的欧氏距离，当两者的欧氏距离小于某一阈值时，即可认为两个特征点是匹配的。图像经常会遭受的旋转、缩放、平移及其组合的仿射变换模型为

式中(w,z)为失真前图像像素的坐标，(x,y)为失真后图像像素的坐标，T为仿射变换矩阵。根据匹配的特征点集可以求出矩阵T中的相关参数，再对失真的图像实施逆变换，即可实现对失真图像的几何校正[10]。

1.2 离散小波变换

在数字图像处理领域，离散小波变换[11]是一种图像的时间频率多尺度分析方法，在时域频域都有表征图像局部特征的能力，并且与新一代国际压缩标准相兼容，用于数字水印中能使水印具有较强的抗压缩能力。图像经过一级小波分解后，会被分解成不同方向，不同分辨率下的四个子带：低频逼近子带(Low Low,LL)、水平高频细节子带(High Low,HL)、垂直高频细节子带(Low High,LH)和对角高频子带(High High,HH)。高频子带体现的是图像的细节信息，即图像的纹理区域，而低频子带包含了图像的主要视觉内容，体现的是图像的概貌特征。

1.3 奇异值分解

一幅灰度图像可以看成是一个由实数组成的二维矩阵，设大小为M×M的灰度图像为A，则图像A的奇异值分解[12]定义为

A=USVT

(1)

其中U，V为大小是M×M的正交矩阵，S是一个非对角线元素都为0的矩阵，对角线上的元素满足以下关系

σ1≥σ2≥…≥σr≥σr+1=…=σM=0。

r为S的秩，这些元素称为图像A的奇异值，式(1)被称为是图像A的奇异值分解。将水印嵌入到奇异值中的理由[13]有：当给图像施加较小额外扰动时，图像的奇异值不会发生很大变化，即图像奇异值稳定性好，且图像的奇异值对几何失真具有不变性。

2 改进的水印算法

算法的主要思想是将水印信息嵌入到载体图像的小波变换域中，同时利用SIFT特征点来提高水印的抗几何攻击能力。载体图像经小波分解后，低频区域集中了图像的大部分能量，包含了图像的主要视觉内容，对各种图像处理攻击都有较好的稳健性，水印嵌入到低频区域会有更好的鲁棒性[14]，但当嵌入的数据过多时会影响水印的不可见性。作为版权保护的水印，本文选择在小波变换的低频域嵌入少量的水印信息，这样既能保持水印的不可见性，又能增强水印的鲁棒性。而将低频系数进行奇异值分解，将加密的水印信息自适应地嵌入到最大奇异值上，可以进一步提高算法的鲁棒性。当水印图像遭受几何攻击时，则用图像的SIFT特征点作为模板校正图像的几何失真，从而达到同步水印信息抵抗几何攻击的目的。提出的算法的具体过程如下。

2.1 水印的嵌入

设选取的载体图像I的大小为M×N，水印图像w的大小为m×n。

(1)图像的加密算法可以极大增强图像的安全性[15]。根据混沌置乱加密理论[16]，利用密钥k1生成一个和水印图像相同大小的混沌矩阵，将混沌矩阵与水印矩阵进行异或加密，然后对加密后的水印图像进行密钥为k2的Arnold置乱加密，从而得到经过高度加密的水印图像wk，保证系统的安全性。

(2)选择小波基为Haar的离散小波变换,将载体图像I进行三级离散小波变换，取其低频子带LL3，把LL3划分为m×n个同样大小的子块B(k),其中k=1,2,…,m×n。

(3)对子块B(k)进行奇偶量化。

(a)先对B(k)进行奇异值分解，得到奇异值矩阵

S=diag(δ1,δ2,…)。

(b)取最大奇异值δ1，根据量化步长q，得到待量化的参数m和自适应调节量化幅度的参数d

(c)水印的嵌入：若

wk(i,j)=0,mod(m,2)=1,

或者

wk(i,j)=1,mod(m,2)=0,

则m可修改为

否则m的值保持不变。

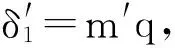
进行相应逆操作，即可得嵌入水印的子块B′(k)。

(5)将B′(k)替换成原来的B(k),再进行三级小波逆变换，即可得到含水印的载体图像Iw，根据前面介绍的SIFT检测方法，提取Iw的SIFT特征点和特征向量作为密钥保存，待水印检测时使用。

2.2 水印的提取

水印的提取是水印嵌入的逆过程，其具体过程如下。

(1)提取出待检测图像的SIFT特征点及其特征向量，结合密钥中保存的特征点和特征向量，求出匹配的特征点，再根据匹配的特征点对之间的相对位置关系校正几何失真的水印图像。

(2)对校正后的图像按嵌入时的步骤进行三级小波分解，将低频子带划分为m×n个子块，依次对每个子块进行奇异值分解，结合量化步长q求出参数m′,根据下式求出加密的水印信息。

w′(i,j)=mod(m′,2),

其中

i=1,2,…,m; j=1,2,…,n。

(3)根据水印混沌置乱加密的密钥k1、k2,解密水印w′(i,j)，即可得到提取出的水印信息w。

3 实验结果

实验采用大小为512×512的灰度图像lena(如图2(a))作为载体图像，大小为32×32的二值图像“陕”(如图2(b))作为水印图像，实验中的量化步长取q=0.2,用峰值信噪比(PeakSignalNoiseRatio,PSNR)和归一化互相关系数(NormalizedcrossCorrelation,NC)来评判算法的优劣。嵌入水印后的lena图像(如图2(c))与原载体图像的PSNR值为42.47，说明本文算法的不可见性较好。在未遭受任何攻击的情况下提取的水印图像(如图2(d))与原水印图像的NC=1，即提取出的水印图像未失真，说明算法的稳健性很好。

图2 载体图像和水印图像

对于常规的信号处理攻击，实验结果如图3所示。图3(a)为添加了强度为0.01的白噪声，图3(b)和(d)则是滤波窗口大小为3×3的高斯低通滤波和中值滤波。图3(c)是压缩质量参数为40%的JPEG压缩。

(a)高斯白噪声 nc=1

(b)高斯低通滤波 nc=0.9981

(c)JPEG压缩40% nc=0.9994

(d)中值滤波 nc=0.9353

从图3可见，提取出的水印NC值都在0.9以上，说明本文的算法能很好地抵抗各种常见的信号处理攻击。然而除了常规的信号处理攻击，水印图像也会经常遭受几何攻击，常见的几何攻击及提取的水印如图4和表1所示。

(a) 旋转10度 nc=0.9598

(b) 缩放1.5 nc=0.9068

(c) 旋转10度+缩放1.5 nc=0.8795

从图4可以看出当NC=0.8594时，提取出的水印视觉效果仍然比较好，而表1中的NC值也都在0.8之上，说明本算法具有了一定的抵抗几何攻击能力。

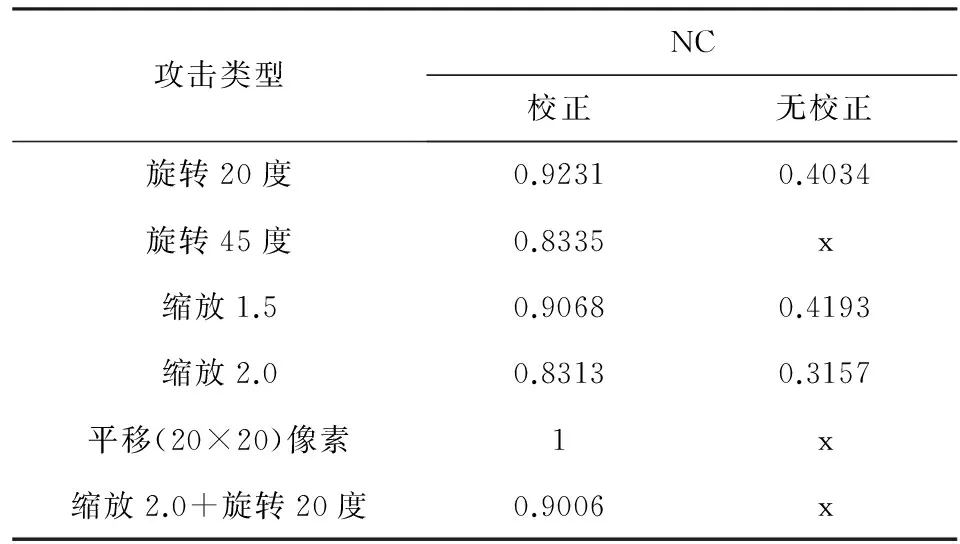
表1 多种几何攻击的实验结果

4 结束语

本文提出了一种基于尺度不变特征变换和离散小波变换的水印算法。算法根据图像SIFT特征点的几何不变性，利用失真前后匹配的SIFT特征点之间的对应关系估算出几何失真参数，校正失真的图像，提高了算法的几何鲁棒性。水印信息嵌入到整个小波变换的低频系数中，在保证系统安全性和鲁棒性的同时，也使系统具有一定的抗裁剪能力。选择在低频系数的奇异值中嵌入水印信息，进一步提高了系统的稳定性。实验结果表明，该算法的运行效率高，水印图像的鲁棒性好，对常见几何攻击，特别是低强度的几何攻击具有很好的鲁棒性。

[1] 李峰，陈光喜，丁勇.基于混沌的Courlet域抗几何攻击图像水印算法[J].计算机应用研究，2012，29(11):4327-4330.

[2] 李昊，吕建平，杨芳芳.基于置乱加密的小波域数字图像水印算法[J].西安邮电学院学报，2009,14(5):107-110.

[3] 胡玉平，王志坚，张玲华，等.基于小波变换和混沌映射的自适应水印算法[J].吉林大学学报，2012,42(1):401-404.

[4] 武峰波，汪峰.基于HVS的小波变换数字图像水印算法[J].应用光学，2014,35(2):254-259.

[5] 吕建平，赵彩霞.基于SVD局部数字水印算法[J].微计算机信息，2010,26(4-3):137-139.

[6]YUYanwei,LINGHefei,ZouFuhao,etal.Robustlocalizedimagewatermarkingbasedoninvariantregions[J].DigitalSignalProcessing, 2012,22(1):170-180.

[7] 邓成，高新波.基于SIFT特征区域的抗几何攻击图像水印算法[J].光子学报，2009,38(4):1004-1010.

[8] 曲巨宝，林宏基.基于特征点密度的DCT域盲检测数字水印算法[J].计算机应用,2011,31(10):2670-2696.

[9]LOWEDG.Distinctiveimagefeaturesfromscaleinvariantkeypoints[J].InternationalJournalofComputerVision，2004,60(2):91-110.

[10] 缪琪男.基于SIFT特征点匹配的水印图像几何校正算法[J].计算机应用研究,2011,28(6):2247-2249.

[11] 黄达人，刘九芬，黄继武.小波变换域图像水印嵌入对策和算法[J].软件学报,2002,13(7):1290-1297.

[12]GuoJingming,PrasetyoHeri.False-positive-freeSVD-basedimagewatermarking[J].JournalofVisualCommunicationandImageRepresentation，2014,25(2014):1149-1163.

[13] 曾晴，马苗，孙莉，等.基于奇异值分解的小波域数字水印方法[J].陕西师范大学学报,2014,42(1):19-23.

[14] 刘思奇，吕建平.视觉系统结合小波域的水印算法[J].西安邮电学院学报，2012,17(2):88-93.

[15] 赵文博，田小平，吴成茂.基于信道编码和Henon映射的图像加密方法[J].西安邮电学院学报，2012,17(3):15-19.

[16]GursharanjeetSK,RajneeshT,HarshS.RobustBlindDigitalImageWatermarkingUsingDWTandDualEncryptionTechnique[C]//2011ThirdInternationalConferenceonComputationalIntelligence,CommunicationSystemsandNetworks.IndonesiaBali：IEEE, 2011:225-230.

[责任编辑:祝剑]

A DWT-domain watermarking algorithm against geometric attacks based on SIFT

LYU Jianping, PENG Shu

(School of Computer Science and Technology, Xi’an University of Posts and Telecommunications, Xi’an 710121, China)

To solve the problem that the image watermarking algorithm based on wavelet transform has poor ability to resist geometric attacks, an improved algorithm is proposed. In this model, a three-level discrete wavelet transform (DWT) decomposition is applied to the cover image, then the watermark is embedded into the max singular value of low frequency coefficient according to the odd-even quantization rules. In order to resist geometric attacks, the geometric distortion parameters with scale invariant feature transform (SIFT) feature points is estimated before the image and extract the watermark is corrected. Experimental results show that the algorithm can resist not only the normal signal processing attacks, such as JPEG compression, noise and filtering, but also geometric attacks, like rotation, scaling and translation.

SIFT,DWT, max singular value, odd-even quantization rules, geometric attacks

2014-09-10

吕建平(1957-)，男，教授，硕士，从事数字图像处理研究。E-mail: lujping1@126.com 彭述(1989-)，男，硕士研究生，研究方向为数字图像处理。E-mail:1099841887@qq.com

10.13682/j.issn.2095-6533.2015.02.016

TP391

A

2095-6533(2015)02-0088-05