有向图出控制数与入控制数的和

郝国亮,钱建国

(厦门大学数学科学学院,福建厦门361005)

有向图出控制数与入控制数的和

郝国亮*,钱建国

(厦门大学数学科学学院,福建厦门361005)

设S是有向图D的一个顶点子集,若D的每个不在S中的顶点都邻接自(到)S的某个(些)顶点,则称S是D的出(入)控制集.D的出(入)控制数是D的出(入)控制集的最小基数.给出了有向图关于出控制数与入控制数之和的上界,部分改进了Chartrand等给出的相应结果.

出控制数;入控制数;有向图

1 预备知识

随着计算机科学和网络通信技术的发展,图的控制集(dominating set)问题的研究受到了较大的关注.对无向图控制集的研究已有较丰富的结果.1968年, Fu[1]把该问题引入到有向图上.较之于无向图,对有向图控制集问题的研究相对较少[2-5].

本文分别用G=(V,E)和D=(V,A)表示简单无向图和简单有向图.如果(u,v)是D的一条弧,则称u邻接到v,或v邻接自u.有向图D中顶点v的出度记为d+D(v),v的入度记为d¯D(v).有向图D的最小出度和最小入度分别为

δ+(D)=min{d+D(v):v∈V(D)},

δ¯(D)=min{d¯D(v):v∈V(D)}.

给定任意图G,对于它的每条边,给其端点指定一个顺序,从而确定一条弧,由此得到一个有向图,这样的有向图称为G的一个定向.一般情况下图G的定向不是唯一的.

设S⊆V(D),若D的每个不在S中的顶点都邻接自(到)S的某个(些)顶点,则称S是D的出(入)控制集.D中包含顶点数最少的出(入)控制集称为D的最小出(入)控制集,它的基数称为D的出(入)控制数,记为γ+(D)(γ¯(D)).显然,入度为0的顶点属于每个出控制集并且出度为0的顶点属于每个入控制集.在此说明:D的出控制集和入控制集也可以分别称为D的控制集和吸收集[6-7].

1999年,Chartrand等在文献[8]中给出了γ+(D)+γ¯(D)的上界:

定理1[8]若D是不含孤立点的n阶有向图,则γ+(D)+γ¯(D)≤4n/3.

受此结果的启发,本文研究有向图的出控制数与入控制数,得到了有向图关于出控制数与入控制数之和的上界,部分改进了Chartrand等给出的相应结果.

2 主要结果及证明

定理3 设D是n阶有向图,且δ¯(D)≥1,则

且此界是可达的.

证明 设H是包含孤立点数最少的D的一个顶点不交的有向星图覆盖.对于整数i≥1,设Hi是由H的所有同构于的连通分支构成的子有向图,并设hi是Hi的连通分支数.显然

易见在D中,H1的任意两顶点间不存在弧,并且也不存在从到V(H1)的弧(否则,与H的假设矛盾).注意到,所以对于H1的任意顶点x,一定存在y∈V(H2)使得(y,x)∈A(D).设阶为2的有向星图uv∈H2,其中u是它的中心.则D中, v最多邻接到H1的一个顶点,并且u不会邻接到H1的任何一个顶点(否则,与H的假设矛盾).考虑到因为δ¯(D)≥1,所以h2≥δ¯(D)h1.

不难看出,S+(H)=V(H1)∪{u:u是Hi(i≥2)中某个有向星图的中心}和S¯(H)=V(H1)∪{u:u是Hi(i≥2)中某个有向星图的非中心的顶点}分别是H的出控制集和入控制集.注意到H是D的生成子有向图,因此

由于

所以

为了说明此界是可达的,设D是顶点不交的3阶有向圈的并,则由定理2可得

利用同样的方法,可以得到下列结果,证明省略.

定理4 设D是n阶有向图,且δ+(D)≥1,则

且此界是可达的.

由定理3和定理4,可以自然地得到:

推论1 设D是n阶有向图,且δ¯(D)≥1, δ+(D)≥1,则

且此界是可达的.

星图Sn是指n≥2阶完全二部图K1,n¯1.星图Sn中最大度顶点称为它的中心.

引理1 设D是星图Sn(n≥2)的定向,且v是Sn的中心,则

2.1.1 检测波长的选择 《中国药典》2015年版记载，SMZ及其制剂定量检测多采用240与254 nm，SDZ及其制剂定量检测多采用260 nm，NOR及其制剂定量检测多采用255～280 nm，OFL及其制剂定量检测多采用290 nm，TC及其制剂定量检测多采用280 nm、OTC及其制剂定量检测多采用280 nm进行检测。为保证待测物质均有较大吸收,本方法采用260 nm为检测波长。

证明 设V(Sn)={v,v1,v2,…,vn¯1}.若.易见{v}和V(Sn) {v}分别是D的最小出控制集和最小入控制集.若则不妨假设

不难验证{v}∪{vi:k+1≤i≤n¯1}和{v}∪{vi: 1≤i≤k}分别是D的最小出控制集和最小入控制集.由此可得

设M是图G的一个边子集,若M中任意两条边都不相邻,则称M是G的匹配.G中最大匹配的基数称为G的匹配数,记作α′(G).

定理5 设D是n≥3阶图G的定向,且G不含孤立点,则

γ+(D)+γ¯(D)≤n+α′(G),

证明 注意到G不含孤立点,因此G含有一个生成子图H使得H的每个连通分支Hi(i∈{1,2,…, k})都同构于某个阶不小于2的星图.对于每个i∈{1,2,…,k},设Di是由V(Hi)导出的D的子有向图.因此由引理1可得γ+(Di)+γ¯(Di)≤|V(Di)|+1,其中i∈{1,2,…,k}.注意到α′(G),所以

为了说明此界是可达的,设D是星图Sn(n≥3)的定向使得其中v是Sn的中心.注意到α′(Sn)=1.因此由引理1可得

设S是图G的一个顶点子集,若S中任意两个顶点都不相邻,则称S是G的独立集.G中最大独立集的基数称为G的独立数,记作α(G).

推论2 设D是n≥3阶二部图G的定向,且G不含孤立点,则

且此界是可达的.

证明 由于G是二部图,所以α′(G)=n¯α(G).由定理5可得

为了说明此界是可达的,设D是星图Sn(n≥3)的定向使得其中v是Sn的中心.注意到α(Sn)=n¯1.因此由引理1可得

定理6 设D是n阶图G的定向,且δ¯(D)≥1, δ+(D)≥1,则

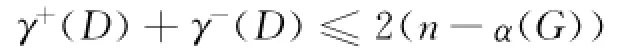
且此界是可达的.

证明 设I是G的一个最大独立集.由于δ¯(D)≥1,所以对于任意的顶点u∈I,至少存在V(D)I中一个顶点邻接到u.因此V(D)I是D的出控制集.另一方面,由于δ+(D)≥1,所以对于任意的顶点u∈I,至少存在V(D)I中一个顶点邻接自u.因此V(D)I也是D的入控制集.由此可得

为了说明此界是可达的,设D是n阶有向圈且G是D的基础图.注意到,由定理2可得

[1] Fu Y.Dominating set and converse dominating set of a directed graph[J].Amer Math Monthly,1968,75:861-863.

[2] Cai H,Liu J,Meng J.Domination number in iterated line digraph of a complete bipartite digraph[J].Ars Combin, 2012,107:515-520.

[3] Niepel L,Knor M.Domination in a digraph and in its reverse[J].Discrete Appl Math,2009,157:2973-2977.

[4] Niepel L,Knor M.Domination in the cross priduct of digraphs[J].Ars Combin,2010,97:271-279.

[5] Pang C,Zhang R,Zhang Q,et al.Dominating sets in directed graphs[J].Inform Sci,2010,180:3647-3652.

[6] Zhang X,Liu J,Chen X,et al.Domination number of Cartesian products of directed cycles[J].Inform Process Lett,2010,111:36-39.

[7] Shan E,Cheng T C E,Kang L.Absorbant of generalized de Bruijn digraphs[J].Inform Process Lett,2007,105: 6-11.

[8] Chartrand G,Harary F,Yue B Q.On the out-domination and indomination numbers of a digraph[J].Discrete Math,1999,197:179-183.

Sum of Out-domination Number and In-domination Number of Digraphs

HAO Guo-liang*,QIAN Jian-guo
(School of Mathematical Sciences,Xiamen University,Xiamen 361005,China)

:A vertex subset S of a digraph D is called an out-dominating(in-dominating)set of D if every vertex outside S is adjacent from(to)some vertexes in S.The out-domination(in-domination)number of a digraph D is the minimum cardinality of an out-dominating(in-dominating)set of D.We obtain some upper bounds on the sum of out-domination number and in-domination number of a digraph,which partially improve the result of Chartrand et al.

out-domination number;in-domination number;digraph

O 157.5

A

0438-0479(2015)03-0351-03

10.6043/j.issn.0438-0479.2015.03.010

2014-04-08 录用日期:2014-10-15

国家自然科学基金(11271307)

*通信作者:guoliang-hao@163.com

郝国亮,钱建国.有向图出控制数与入控制数的和[J].厦门大学学报:自然科学版,2015,54(3):351-353.

:Hao Guoliang,Qian Jianguo.Sum of out-domination number and in-domination number of digraphs[J].Journal of Xiamen University:Natural Science,2015,54(3):351-353.(in Chinese)