基于多结构估计的建筑物激光雷达点云特征线提取算法

江 静,蔡国榕,陈水利,李绍滋,吴云东*

(1.集美大学理学院,福建厦门361021;2.厦门市无人机遥感应用工程技术研究中心,福建厦门361021; 3.厦门大学信息科学与技术学院,福建省仿脑智能系统重点实验室,福建厦门361005)

基于多结构估计的建筑物激光雷达点云特征线提取算法

江 静1,2,蔡国榕1,2,陈水利1,2,李绍滋3,吴云东1,2*

(1.集美大学理学院,福建厦门361021;2.厦门市无人机遥感应用工程技术研究中心,福建厦门361021; 3.厦门大学信息科学与技术学院,福建省仿脑智能系统重点实验室,福建厦门361005)

建筑物激光雷达(light detection and ranging,LiDAR)点云特征线对于多视角点云配准、建筑物对称性检测、建筑物三维重建等应用具有十分重要的意义.由于LiDAR点云具有数据量庞大的特点,传统的算法难以实现建筑物特征线的快速提取.针对这个问题,提出一种基于多结构鲁棒估计的建筑物特征线提取算法,该算法利用历史模型信息进行条件采样,并通过迭代搜索符合所有特征线性质的模型.根据建筑物LiDAR数据的实验结果表明,该方法与传统的RANSAC(random sample consensus)、MLESAC(maximum likelihood estimation sample consensus)等算法相比,避免了无效、重复的特征线采样过程,在相同时间内可获取更多的直线内点,从而有效提高了建筑物特征线的提取效率.

激光雷达点云;特征线提取;多结构;相似函数

激光雷达(light detection and ranging,LiDAR)获取的三维数据不仅具有精度好、密度高、处理成本低的优点,且其数据获取过程中不受光照变化、阴影和天气因素的影响.因此,相关数据处理技术已逐渐成为遥感、测绘、计算机视觉等领域新的研究热点.由于LiDAR扫描得到的点云数据量很大,为了加快处理速度,一般需要对点云进行抽稀或特征提取,以减少点云数量.其中,点云特征线提取是提高建筑物配准、重建效率的有效工具.

点云特征线是由扫描物体上尖锐特征,或高曲率部分采样特征点组成的线段或曲线.目前,三维模型特征线提取技术已被广泛用于增强建筑物点云的几何特征[1]、对称性检测[2]、表面重建[3]、点云分割[4]、曲线匹配、模型简化以及点云与图像的配准等[5].点云数据特征线提取方法主要包括:1)基于三角网格在对曲率信息估计的基础上提取特征线[6-7];2)最小生成树法:Gumhold等[8]在对所有点构建邻域关系的黎曼图基础上,计算每个点的特征权重将点进行分类,最后由黎曼图的最小生成树来生成特征线.Pauly等[9]通过在多尺度上对特征进行分析拓展了此方法;3)李宝等[10]用RANSAC提取特征点,然后用主成分分析的方法计算线段参数来提取特征线;4)折线生长算法:在提取已有特征点基础上,由用户输入一个半径值来控制特征折线的精度,然后用主成分分析方法完成特征折线的生成.这些方法在处理噪声数据和缺失数据方面存在局限性,特别是处理LiDAR数据的时间代价偏高,难以满足特征线快速提取的需求.

目前在LiDAR数据上提取建筑物特征线一般是将LiDAR点云数据转化为深度图像,再利用图像的分割算法及边界线提取算法提取特征线[11-12].梁欣廉[13]使用分裂的最小均方差线段逼近法,从离散的LiDAR数据中提取建筑物特征线.尤红建等[14]用方位角分离出靠近建筑物轮廓边缘上的激光点,对分离出的激光点进行规则化处理,同时依据边缘点连线方向角度的变化进行边界点的分组,计算建筑物的主方向,然后对边界点进行边缘规则化,最后得到建筑物最外侧边缘的轮廓.分析目前基于LiDAR点云数据提取建筑物特征线的研究工作,主要集中在处理凸多边形数据,针对凹多边形轮廓特征线的处理方法有限且效果不理想.现有方法需要用到迭代逼近,本身运算量较大,又因为LiDAR数据具有海量的特点,因此处理效率有待提高.

针对以上算法存在的效率问题,本文首先根据文献[15]方法,提取建筑物LiDAR点云数据的特征点.在此基础上,计算特征点对假设模型的残差,利用残差排序构造两点属于同一模型的相似函数.采样过程中利用相似函数构造的条件概率进行采样,使采样朝着同一直线上的点进行.当采样到一定模型集后放入原模型集重新计算残差,更新模型集使之向最优的模型方向迭代.算法利用相似性函数指导采样,降低了RANSAC、MLESAC等随机采样在LiDAR海量数据中重复计算的风险,提高了采样速度.通过点对模型的残差排序情况来确定点属于某个模型的可能,有效减少了LiDAR数据噪声点和非均匀点对模型产生的影响.与以往算法借助三角网格和图像提取点云特征线的主要区别在于,本文直接对LiDAR扫描的数据进行处理,降低了算法的复杂度,有效提高了处理效率.实验结果表明由Chin等[16]提出的多结构模型快速生成算法在采样速度、局内点总数以及鲁棒性方面比随机采样RANSAC[17]、MLESAC[18-19]算法有较大提高.

1 多结构算法提取建筑物LiDAR点云特征线

本文利用多结构算法直接对LiDAR建筑物点云数据进行处理,通过点对模型的残差构造相似函数来指导模型采样,降低了噪声和数据的不均匀因素对模型产生的影响.指导性采样的过程为海量LiDAR数据节省了采样时间,增加了模型获得内点数目,提高了模型提取的准确率和速度.

1.1 多结构模型算法的基本原理

多结构模型快速生成算法是一种鲁棒性估计方法,该算法通过计算数据点对假设模型的残差,对残差进行排序,然后构造数据点之间的相似函数,用来度量数据点之间属于同一结构的相似程度,以此来指导采样,当产生一定数量的新模型后,将其融入原模型集,再利用条件概率有指导地采样,使其向最优的模型方向迭代.

在有序残差的基础上,定义xi和xj的相似函数:表示xi和xj残差升序排序后前h个模型中相同模型的个数.由于的取值范围为[0,1]且是对称的,对于所有的i,有f(xi,xi)=1.h为点按照模型残差值排序的前n(n=1,2,…,M)个模型,在文献[16]中知h的取值范围为1≤h≤M.

利用残差排序和相似函数,在规定时间范围内来指导模型取样,主要采用条件概率的方法选取特征点,构造优化模型.随机选择第一个数据点s1,在此基础上,通过条件概率

选择第2个数据点s2,a1是归一化因子,a1=保证P1(i)为有效的离散条件概率分布,则s2的选取概率依赖于P1,即s2～P1.同理,假设选择每个点都是独立的,根据贝叶斯原则,后续点的选取依赖于与被选中点之间的相似度.即

其中ak也是归一化因子,则第s+1个数据点的选择概率依赖于Pk,即sk+1～Pk.

输入 点云数据集X,需要的总模型个数T,最小子集p,改变窗口大小的模型个数b,采样模型集Θ1,控制相似函数大小的h,残差阈值ζ

输出 模型Θ

第1步:如果模型个数M≤b,则随机取样p个数据点并存储在矩阵S中;

第2步:随机采样模型,使得模型个数M＞b,放入模型集Θ1中,点集X中随机选择第一个点s1,存储矩阵S中;

第3步:根据采样的第1个点s1,利用a(i),h构造公式P1(i),来采样模型需要的第2个点s2,并放入矩阵S中,利用已采样的点构造概率矩阵Pk(i)来采样下一个点,直到采样p个点为止.本文中直线模型只需采样两个点;

第4步:将第3步采样得到的由p个点构成的模型放入模型集Θ1中.循环第2步到第4步直到采样到T个模型;

第5步:如果模型个数M≥b并且mod(M,b)= 0,将采样的模型Θ1加入到模型Θ中,重新计算点对所有模型的残差,并进行排序得到a(i).统计每个模型对数据点的残差值小于阈值ζ的个数,个数最多的模型为最优的直线模型Θ,改变h的大小,h=[0.1M].

1.2 线段检测

多结构模型算法用于检测直线模型,直线生成算法如下:

输入 三维点云数据点集P={pi},模型个数M,距离阈值,得分阈值

输出 三维直线Imo的参数a,b,c,x0,y0,z0

第1步:在P中随机选择一点Pm1,根据多结构中条件概率选择另外一点Pm2;

第3步:计算P中其余点Pj到Im的距离dj,存入矩阵dt中;

第4步:重复步骤1～3共M次,选择出M个模型;

第5步:统计P中其余点Pj到每个模型的距离dj小于阈值ζ的点作为直线Im的内点,并统计它的个数,作为Im的得分FIm;

第8步:重复步骤1～7直到无法从剩余点中选择一个得分至少为阈值F′0的直线.

检测出直线后,需要将位于同一条直线上不同的目标线段找出来,实现窗户边缘特征,算法过程如下:

输入 通过算法1检测出的属于同一直线上的点集Q={qi},距离阈值α和点数阈值γ

第1步:如果输入点集Q={qi}的max X¯min X绝对值小于阈值α,则输入的点属于竖直直线上的点;

第2步:按照z值对这些点排序,并计算相邻的两点之间的距离;

第3步:如果相邻两点之间的距离小于阈值β,则保存这相邻的两点到矩阵inx,继续下一个两点之间距离的检测;

如果相邻两点之间距离大于阈值β,检测矩阵inx是否为空,如果inx为空或者inx点的数量小于阈值γ,则将inx中的点的索引全设为0,继续步骤3,检测下面的点;

否则画出检测出来的线段,将inx中的点的索引重新设为0,继续步骤3;

第4步:检测剩下的点,如果inx是空或者inx中点的索引小于阈值γ,则返回;

否则画出直线段;

水平方向检测max Z¯min Z的绝对值是否小于阈值α,其他步骤和竖直方向一样.

取ζ=0.065,F′0=15,α=0.25,β=0.4,γ=15实验效果为最佳.

2 实验结果与分析

本文采用vs2010平台对LiDAR点云数据构建kd_tree,提取特征点,然后利用MATLAB 2011a作为仿真平台,对本文提出的算法进行实现.实验中改变窗口大小的模型个数b=10.

图1(a)为RIGEL固定站式激光扫描仪扫描的建筑物立面墙点云数据,总点数X=89 498,图1(b)为采用切割最小二乘平面算法提取的特征点,提取的特征点数为9 605个,图1(c)为多结构算法在有限时间lim=1时提取的标准特征线,为下面在不同时间限制内的实验结果提供参考,模型个数上限T=2 000,点数阈值γ=15,图2 lim=0.5,T=20,γ=100;图3 lim =0.6,T=100,γ=15.图2和3分别为不同限制时间内RANSAC、MLESAC和多结构算法提取的特征线图,可以看出在有限时间内,当模型个数上限分别为20和100的情况下,RANSAC和MLESAC算法寻找最优直线的能力均不及多结构算法,而且随着模型个数和时间的增多,多结构算法检测的特征线图更趋于标准特征线图.

图4中(a)是与图1(a)在不同站点下扫描的点云数据.图4(a)中总点数X=3 215,图4(b)中用切割最小二乘平面算法提取的特征点,个数为945个,图4 (c)为用多结构算法提取的标准特征线图,T=200, lim=2,γ=15.图5和6中时间限制分别为0.006和0.01,模型上限T均为10,γ=15.图5和图6为在点数较少情况下所做实验,可以看出,相同较短时间下,多结构算法能有效利用历史模型信息提取较多特征线,且提取的特征线较完整,而RANSAC和MLESAC算法提取的特征线较破碎.

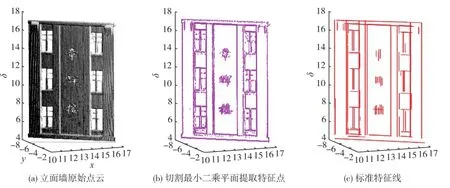
图1 标准特征点、特征线,有限时间lim=1Fig.1 Standard feature points,feature lines with limit time of 1

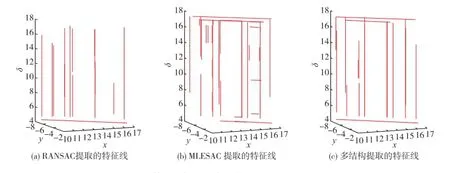
图2 不同算法下提取的特征线对比,有限时间lim=0.5Fig.2 Feature lines comparison of different algorithms with limit time of 0.5

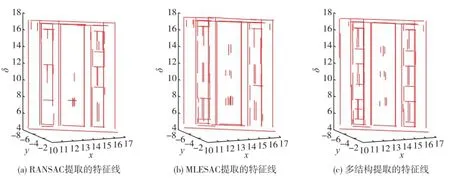
图3 不同算法下提取的特征线对比,有限时间lim=0.6Fig.3 Feature lines comparison of different algorithms with limit time of 0.6

图7 为最优直线所包含的内点个数.从图中可以看出检测同一条直线,多结构算法包含内点能力优于其他2种算法.随着提取直线个数的增多,直线包含内点个数逐渐减少.表1为多结构算法和其他2种算法实验参数的对比,由于多结构算法利用残差排序构造两点之间相似函数,利用相似函数建立已采样点的联合概率模型,估计下一个采样点的概率,不断更新采样模型使其向最优的模型方向迭代.在相同时间内多结构算法利用指导采样比RANSAC和MLESAC等随机采样算法提取的特征线条数更多,更接近标准特征线,迭代次数更少,寻找到最优直线所用时间更短.

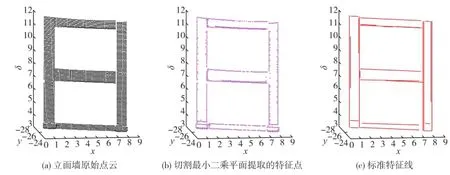
图4 标准特征点、特征线,有限时间lim=2Fig.4 Standard feature points,feature lines with limit time of 2

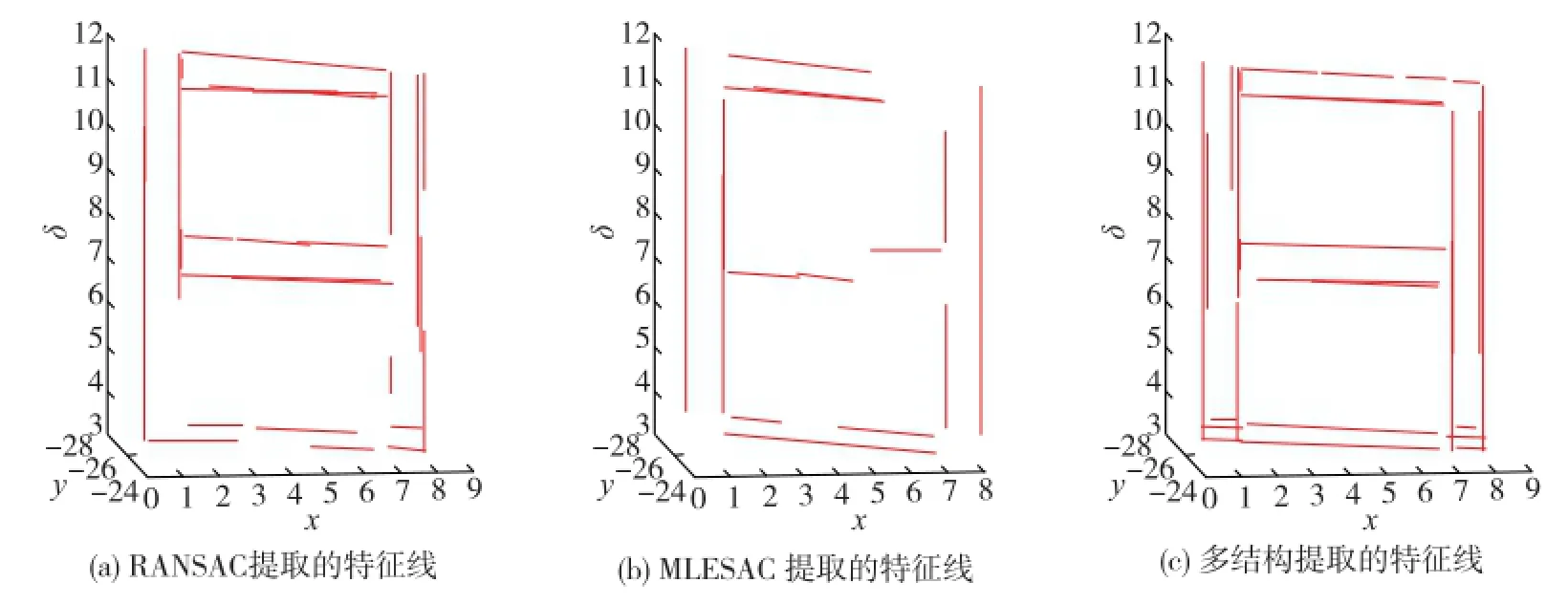
图5 不同算法下提取的特征线对比,有限时间lim=0.006Fig.5 Feature lines comparison of different algorithms with limit time of 0.006

图6 不同算法下提取的特征线对比,有限时间lim=0.01Fig.6 Feature lines comparison of different algorithms with limit time of 0.01

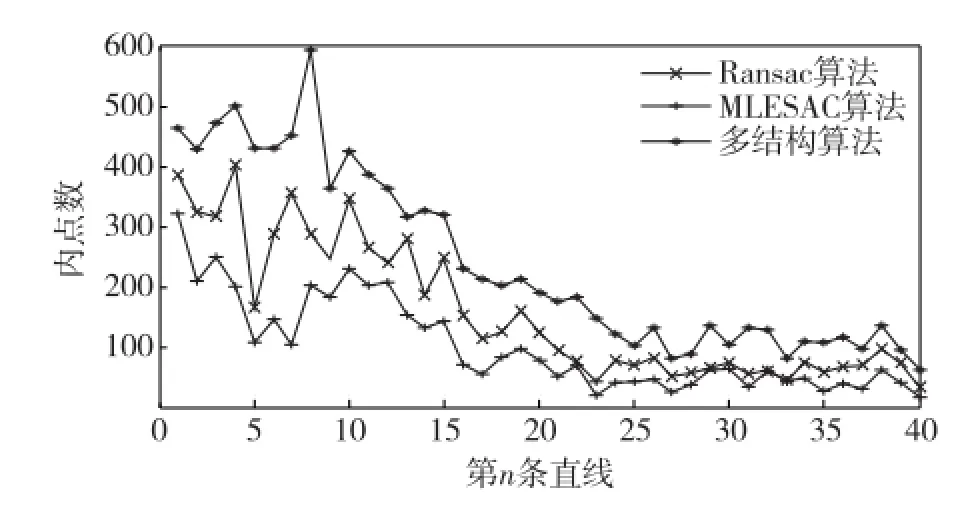
图7 最优模型内点个数Fig.7 Number of optimal model inlier

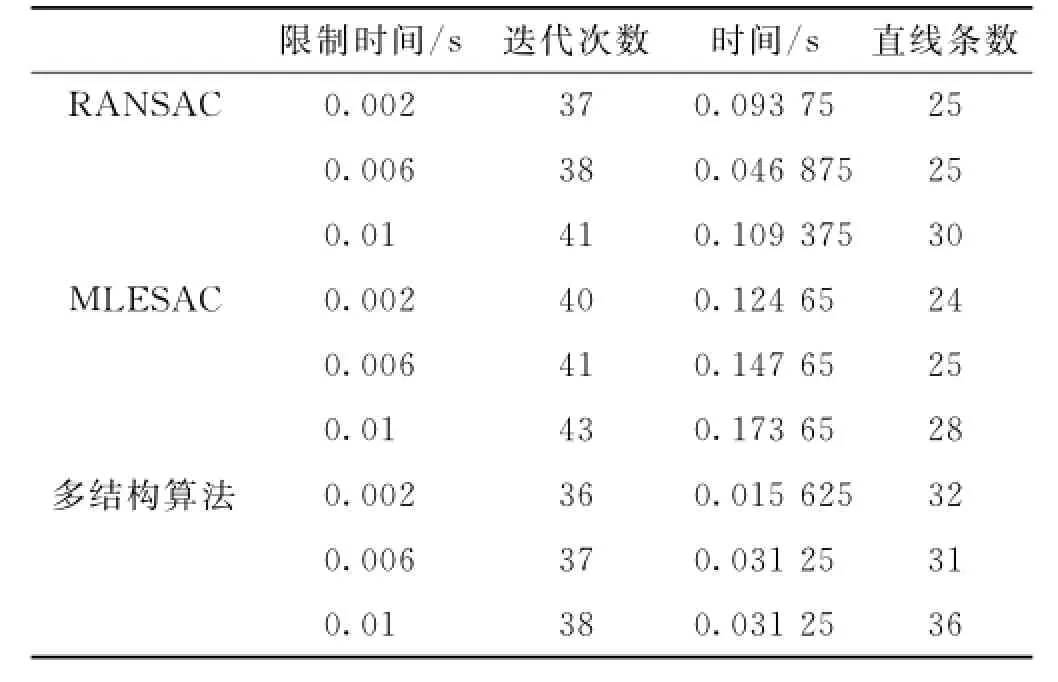
表1 两算法参数对比,其中T=10,γ=5Tab.1 Comparison parameter of two algorithm,T=10,γ=5

3 结 论

本文针对建筑物立面墙LiDAR点云数据的特征线提取问题,在建立点云数据kd_tree的基础上,引用文献[15]中的方法提取立面墙边界特征点,然后提出基于多结构鲁棒估计的建筑物LiDAR点云特征线提取算法.算法直接作用于建筑物点云数据,在有限时间内,该算法能有效利用历史模型信息,建立已采样点的联合概率,来对下一个采样点进行估计,如此进行指导采样,不断更新采样模型使其向最优的方向迭代.实验结果表明:本算法能根据模型残差排序进行指导采样,有效增强了算法找出最优直线模型的能力,提高了寻找最优直线的速度和效率,寻找最优直线所包含内点的能力比其它两种算法有优势.在处理特征点采样问题时,其采样性能优于RANSAC、MLESAC算法.

[1] Merigot Q,Qvsjanikov M,Guibas L.Voronoi-based curvature and feature estimation from point cloud[J].IEEE Transactions on Visualization and Computer Graphics, 2011,17(6):743-756.

[2] Bokeloh M,Berner A,Wand M,et al.Symmetry detection using feature lines[J].Computer Graphics Forum,2009, 28(2):697-706.

[3] Xue T,Liu J,Tang X.Example-based 3D object reconstruction from line drawings[C]∥Computer Vision and Pattern Recognition.Providence,RI:IEEE,2012: 302-309.

[4] Weber C,Hahmann S,Hagen H.Sharp feature detection in point clouds[C]∥Shape modeling international conference(SMI).Aix-en-Provence:IEEE,2010:175-186.

[5] Liu L,Ioannis S.A systematic approach for 2D-image to 3D-range registration in urban environments[J].Computer Vision and Image Understanding,2012,116(1):25-37.

[6] Hilderandt K,Polthier K,Wardetzky M.Smooth feature lines on surface meshes[C]∥Symposium on Geometry Processing.Switzerland:ACM Press,2005:85-90.

[7] Ohtake Y,Belyaev A,Seidel H P.Ridge-valley lines on meshes via implicit surface fitting[J].SIGGRAPH,2004, 23(3):609-612.

[8] Gumhold S,Wang X,Mcleod R.Feature extraction from point clouds[C]∥Proceedings of the 10th International Meshing Roundtable.Berlin:Springer Press,2001: 293-305.

[9] Pauly M,Gross M.Multi-scale feature extraction on point-sampled surfaces[J].Computer Graphics Forum, 2003,22(3):281-289.

[10] 李宝,程志全,党岗,等.一种基于RANSAC的点云特征线提取算法[J].计算机工程与科学,2013,35(2): 147-153.

[11] Li S K,Xue Y Q.Efficiently 3D remote sensing integration system[M].Beijing:Science Press,2000.

[12] Brian B J,Hanson A R,Riseman E M.Extracting straight lines[J].IEEE Pattern Analysis and Machine Intelligence,1986,8(4):425-455.

[13] 梁欣廉.机载激光雷达数据滤波与建筑三维模型重建[D].北京:中国测绘科学研究院,2005.

[14] 尤红建,李树凯.基于稀疏激光采样点的建筑物提取[J].中国科学院研究生院学报,2001,18(2):154-158.

[15] 钱锦锋,陈志杨,张三元,等.点云数据压缩中的边界特征检测[J].中国图像图形学报,2005,10(2):164-169.

[16] Chin T,Jin Y,David S.Accelerated hypothesis generation for multi-structure data via preference analysis[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,2011,34(4):625-638.

[17] Martin A,Robert C.A paradigm for model fitting withapplications to image analysis and automated cartography[J].Comm of the ACM,1981,24(6):381-395.

[18] Torr P H S,Zisserman A.MLESAC:a new robust estimator with application to estimating image geometry [J].Computer Vision and Image Understanding,2000, 78(1):138-156.

[19] Rastgar H,Liang Z,Demin W,et al.Validation of correspondences in MLESAC robust estimation[C]∥IEEE International Conference Computer Vision and Pattern Recognition.Tampa,FL:IEEE,2008:1-4.

Extract Feature Lines from Building LiDAR Point Cloud Based on Multi-structure Estimators

JIANG Jing1,2,CAI Guo-rong1,2,CHEN Shui-li1,2,LI Shao-zi3,WU Yun-dong1,2*
(1.College of Science,Jimei University,Xiamen 361021,China;2.Engineering Technology Research Center of UAV Remote Sensing Application,Xiamen 361021,China;3.Fujian Key Laboratory of the Brain-like Intelligent Systems,School of Information Science and Engineering,Xiamen University,Xiamen 361005,China)

:Feature lines extracted from building LiDAR(Light Detection and Ranging)point cloud data are of great significance in multiple views registration,building symmetry detection,3D surface reconstruction,among others.Since the LiDAR data are generally associated with a huge amounts of 3D points,traditional algorithms suffer from the time complexity of rapidly extracting feature lines from building point cloud.In order to solve this problem,we present a feature lines extracted algorithm based on multi-structure robust estimation.In the proposed method,historical models generated by random strategy have been used for conditional sampling new models.Consequently,the searching process aims at extracting all feature lines from the model set.In the section of experiments, the multi-structure algorithm has been compared with the RANSAC(random sample consensus)and MLESAC(maximum likelihood estimation sample consensus).Results acquired from our LiDAR dataset indicate that the proposed method improves the efficiency of building feature lines extraction,since the multi-structure algorithm avoids many invalid and repeated sampling processes.Therefore, we can generate more feature lines at the same time.

LiDAR point clouds;feature lines extraction;multi-structure;similar function

O 29;P 231

A

0438-0479(2015)03-0390-07

10.6043/j.issn.0438-0479.2015.03.018

2014-07-31 录用日期:2014-10-27

国家自然科学基金(61103052);国家科技支撑计划(201309110001);国家高技术研究发展计划(863计划)(2012AA12A208-06);福建省产学重大科技项目(2011H6020);福建省自然科学基金(2012J01013,2013J01245);福建省教育厅专项课题(JK2012025);厦门市科技计划项目(3502Z20110010)

*通信作者:yundongwu@jmu.edu.cn

江静,蔡国榕,陈水利,等.基于多结构估计的建筑物激光雷达点云特征线提取算法[J].厦门大学学报:自然科学版, 2015,54(3):390-396.

:Jiang Jing,Cai Guorong,Chen Shuili,et al.Extract feature lines from building LiDAR point cloud based on multi-structure estimator[J].Journal of Xiamen University:Natural Science,2015,54(3):390-396.(in Chinese)