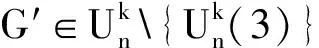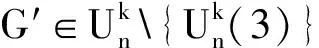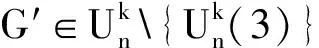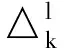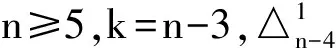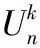最小Q-特征值第二小的给定悬挂点数的非二部单圈图
2015-06-23刘晓蓉
刘晓蓉,张 荣
(1.青海师范大学 数学系,青海 西宁 810008; 2. 盐城师范学院 数学与统计学院,江苏 盐城 224002)
最小Q-特征值第二小的给定悬挂点数的非二部单圈图
刘晓蓉1,2,张 荣2
(1.青海师范大学 数学系,青海 西宁 810008; 2. 盐城师范学院 数学与统计学院,江苏 盐城 224002)
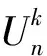
非二部单圈图;悬挂点;最小特征值
令G=(V,E)是一个简单无向图,它的顶点集V=V(G)={v1,v2,…,vn},边集E=E(G)。A(G)为图G的邻接矩阵,D(G)=diag{d(v1),d(v2),…,d(vn)}为G的度对角矩阵,这里d(vi)是顶点vi的度,称矩阵Q(G)=D(G)+A(G)为G的拟(无符号)拉普拉斯矩阵(又称Q-矩阵)。因为D(G)是半正定矩阵,所以它的特征值都为非负实数,可排列为q1(G)≥q2(G)≥…≥qn(G)≥0,我们称Q(G)的特征值为图G的拟拉普拉斯特征值或Q-特征值。
对于一个连通图来说,它的最小Q-特征值为零当且仅当它是二部图。Desai等[1]讨论了图的最小Q-特征值与图的二部性之间的关系,建议用最小Q-特征值来衡量一个图的非二部程度;Fallat等[2]将图的最小Q-特征值定义为图的代数二部度(algebraic bipartiteness),引入图的点二部度、边二部度概念,并建立了与代数二部度的联系;Cardoso等[3]确定了最小Q-特征值达到最小的n阶非二部连通图为三圈的一个顶点上接出一条路所得到的图;汪毅等[4]研究了图的一个偶分支从一个顶点移接到另一个顶点时图的最小Q-特征值,并证明了最小Q-特征值的一个扰动定理,由此刻画了在含有某个给定非二部图作为诱导子图的连通图类中最小Q-特征值达到最小的图的结构。此后,人们先后对许多非二部连通图类和非二部单圈图类确定了最小Q-特征值达到最小的图[2,4-11]。
单圈图是边数等于顶点数加1的简单连通图。对于给定阶数和悬挂点数的非二部单圈图,范益政等[12]确定了最小Q-特征值达到最小的图,本文继续研究给定阶数和悬挂点数的非二部单圈图,确定了最小Q-特征值达到第二小的图。
1 预备知识
Cn和Pn分别表示阶为n的圈和路。令G-u,G-uv,分别表示G中去掉顶点u和去掉边uv后得到的图。同样地,G+uv表示在图G中增加边uv∉E(G)得到的图,这里u,v∈V(G)。度为1的顶点称为图G的悬挂点,邻接于悬挂点的顶点称为G的悬挂邻点,与悬挂点关联的边称为G的悬挂边。对于v∈V(G),NG(v)定义为图G中顶点v的所有邻点组成的集合,我们用dG(u,v)(或d(u,v))表示G中顶点u和v之间的距离,这里u,v∈V(G)。
令x=(x1,x2,…,xn)T∈Rn,那么x可以看成是定义在V(G)上的一个函数,也就是说x是顶点vi到xi=x(vi)的映射。如果x是对应于某个Q-特征值的特征向量,那么x(v)可自然地看成是x中对应于v的分量。不难看出
(1)
进而,对于任意一个单位向量x∈Rn,由对称矩阵的特征值性质知
qn(G)≤xTQ(G)x
等号成立当且仅当x是对应于qn(G)的一个特征向量。
令G1和G2是两个不相交的图,v1∈V(G1),v2∈V(G2)。G1和G2的粘合(coalescence)用G1(v1)◇G2(v2)来表示,它是由G1和G2通过重合顶点v1和v2形成一个新的顶点u而得到的图(详见文献[5])。图G1(v1)◇G2(v2)也可以写成G1(u)◇G2(u)。如果连通图G可以表示成G1(u)◇G2(u),这里G1和G2都是非平凡且连通的,那么分别称G1和G2为图G的根点为u的一个分支。设x是定义在G上的向量,H是G的一个分支,如果对应于向量x,对任意顶点p∈V(H),都有x(p)=0成立,则称H是G的对应于向量x的零分支;否则称H为对应于向量x的非零分支。
引理1[4]设G为n阶连通图,它包含以u为根点的二部图H,如果x=(x1,x2,…,xn)T是G的对应于qn(G)的特征向量,则
(i)若x(u)=0,则H是对应于x的零分支;
(ii)若x(u)≠0,则对任意的p∈V(H),有x(p)≠0。
引理2[4]设G是n阶非二部连通图,x是对应于qn(G)的特征向量,T是以u为根点对应于向量x的非零分支,则|x(q)|<|x(p)|,其中p,q为T的两个顶点,且q在从u到p的唯一路上。
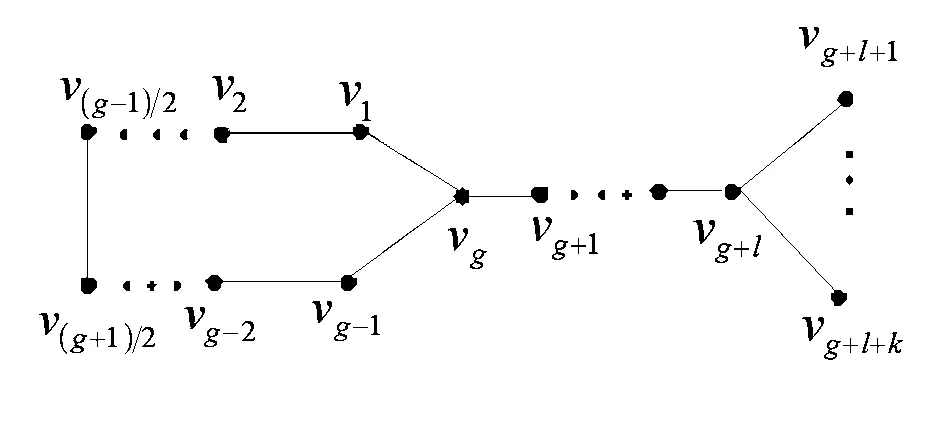
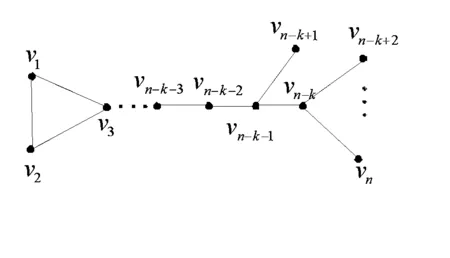
引理3[9]设G=G1(v2)◇T(u),G*=G1(v1)◇T(u)为2个n阶图,其中G1是一个包含2个不同顶点v1,v2的非二部连通图,T是一棵非平凡树。如果存在对应于qn(G)的特征向量x=(x(v1),x(v2),…,x(vn))T,使得|x(v1)|>|x(v2)|或|x(v1)|=|x(v2)|>0,那么qn(G*) 引理4[9]设G=C(v0)◇B(v0),其中C=v0v1v2…vkukuk-1…u1v0是一个长为2k+1的圈,B是一个阶数为n-2k的偶图,如图1所示,那么存在关于qn(G)的一个特征向量x=(x(v0),x(v1),x(v2),…,x(vk),x(u1),x(u2),…,x(uk),…)T,满足 (i)|x(v0)|=max{|x(w)||w∈V(C)}>0; (ii)x(vi)=x(ui),i=1,2,…,k; (iii)x(vi)x(vi-1)≤0,x(ui)x(ui-1)≤0,i=1,2,…,k。 图1 C(v0)◇B(v0)Fig.1 C(v0)◇B(v0) 此外,若2k+1 图Fig. 图Fig. 首先,我们断言G是圈Cg=v1v2…vgv1的某个顶点上接出一棵非平凡树得到的,否则,我们假设G是圈Cg上s(≥2)个不同顶点处接出非平凡树而得到的。假设vt是圈Cg上的一个顶点使得|xt|≥|xi|,i=1,2,…,g,则由引理1知,xt≠0,否则,可得x=0,与x为特征向量矛盾。设vl是圈Cg上的另一顶点,在vl处接出一棵非平凡树,令 其次,我们断言g=3,否则,我们假设g≥5,根据引理3可知x(g-3)/2=x(g+3)/2。令 令vt是G的一个悬挂点,假设y=(y1,y2,…,yn)是对应于qn(G′)的单位特征向量,根据引理2,有|y(vt)|>|y(vg)|>0。令 G″=G′-v1vg+v1vt 第五,我们断言va和vb是相邻的,否则,我们假设va和vb是不相邻的。令vc∈NG(vb)是vb-va上的一个顶点,那么根据引理2,有|xc|>|xb|。令vt是邻接于vb的悬挂邻点,并且 G′=G-vbvt+vcvt 最后,我们断言d(vb)=3。否则,假设 d(vb)>3。令vt是邻接于vb的悬挂邻点,并且 G′=G-vbvt+vcvt 其次,我们断言d(v2)=3,否则,假设 d(v1)≥d(v2)>3。若|x1|<|x2|,则d(v1)>d(v2)>3。在顶点v1处去掉d(v1)-d(v2)悬挂边,在顶点v2处增加d(v1)-d(v2)悬挂边,所得到的图记为G′。根据引理3可得,qn(G)>qn(G′),但显然G=G′,产生矛盾,从而|x1|≥|x2|,vs是v2的一个悬挂点。令 G*=G-v2vs+v1vs [1] Desai M, Rao V. A characterization of the smallest eigenvalue of a graph[J].J. Graph Theory, 1994,18(2):181-194. [2]FallatS,FanYZ.BipartitenessandtheleasteigenvalueofsignlessLaplacianofgraphs[J].LinearAlgebra&ItsApplications, 2012,436(9):3 254-3 267. [3]CardosoDM,CvetkovicD,RowlinsonP,etal.AsharplowerboundfortheleasteigenvalueofthesignlessLaplacianofanon-bipartitegraph[J].LinearAlgebra&ItsApplications, 2008,429(11-12):2 770-2 780. [4]WangY,FanYZ.TheleasteigenvalueofsignlessLaplacianofgraphsunderperturbation[J].LinearAlgebra&ItsApplications,2012,436(7):2 084-2 092. [5]LimaLSD,OliveiraCS,AbreuNMMD,etal.ThesmallesteigenvalueofthesignlessLaplacian[J].LinearAlgebra&ItsApplications, 2011,435(10):2 570-2 584. [6]FanYZ,TanYY.TheleasteigenvalueofsignlessLaplacianofnon-bipartitegraphswithgivendominationnumber[J].DiscreteMath, 2014,334(334):20-25. [7]LiS,WangS.TheleasteigenvalueofthesignlessLaplacianofthecomplementsoftrees[J].LinearAlgebra&ItsApplications, 2012,436(7):2 398-2 405. [8]LiuR,WanH,YuanJ,etal.TheleasteigenvalueofthesignlessLaplacianofnon-bipartiteunicyclicgraphswithkpendantvertices[J].ElectronJ.LinearAlgebra, 2013,26(2):333-344. [9]YuGL,GuoSG,XuML.OntheleastsignlessLaplacianeigenvalueofsomegraphs[J].ElectronJ.ofLinearAlgebra,2013,26(8):560-573. [10]YuG,GuoSG,ZhangR,etal.ThedominationnumberandtheleastQ-eigenvalue[J].AppliedMathematics&Computation,2013,244(2):274-282. [11]YuGD,FanYZ,WangY.QuadraticformsongraphswithapplicationtominimizingtheleasteigenvalueofsignlessLaplacianoverbicyclegraphs[J].Electron,J.LinearAlgebra, 2014,27(3):213-236. [12]FanYZ,WangY,GuoH.TheleasteigenvaluesofsignlessLaplacianofnon-bipartitegraphswithpendantvertices[J].DiscreteMath,2012,313(7):903-909. (责任编辑:张英健) The Non-bipartite Unicyclic Graph with Fixed Number of Pendent Vertices Whose Least Q-eigenvalue Attains the Second Smallest LIU Xiaorong1,2, ZHANG Rong2 (1.Department of Mathematics, Qinghai Normal University, Xining Qinghai 810008, China;2.School of Mathematics and Statistics, Yancheng Teachers University, Yancheng Jiangsu 224002, China) Non-bipartite unicyclic graph; Pendant vertices; Least eigenvalue 10.16018/j.cnki.cn32-1650/n.201504003 2015-05-20 国家自然科学基金资助项目(11171290);江苏省自然科学基金(BK20151295) 刘晓蓉(1990-),女,青海同仁人,硕士生,主要研究方向为图论。 O157.5 A 1671-5322(2015)04-0011-04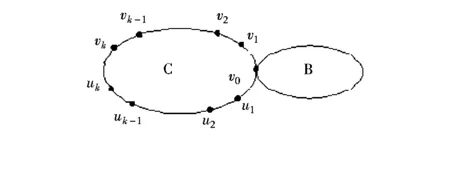
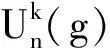
2 主要结果