高考数学“最值”问题

湖北省宜城一中 严 帆

最值作为高中数学的一个重要内容，一直是高考考查的重点，也是高考考查的一个难点，下面就一些最值问题作出分析。

最值问题一般可分为两种形式，一是函数的最值；二是多项式的最值。

一、函数的最值

函数是高中数学的基础内容，它贯穿于整个高中数学知识，而最值又是函数最重要的问题，因此在高考中经常考查，考查形式大致有两种：直接求函数的最值；恒成立问题转化为求函数最值。

1．直接求函数最值

对基本初等函数或由基本初等函数复合而成的简单函数的最值。

如：已知的最值。

解：由题可得：

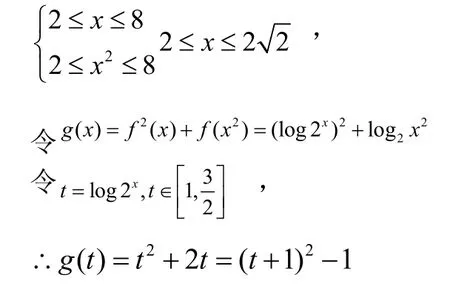
此时此时

∴当最大值为当x=2时，最小值为3。

该题为二次函数与对数函数的复合函数，求其最值，首先注意找出定义域，这也是我们解决函数问题的基本要求，然后利用换元法将求原函数的最值转化为求二次函数的最值，结合基本初等函数的性质求解，其常见的求解方法还有配方法、判断式法等。

又如求函数在上的最大值，最小值。

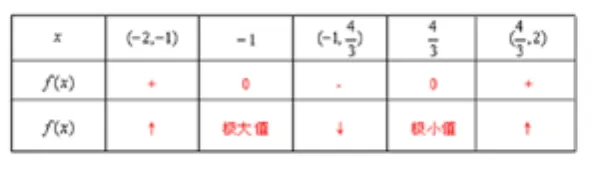
又

函数f(x) 最大值为最小值为

对于解析式较复杂的一类连续函数的最值的求解可以利用导数来求解。

2．恒成立问题转化为求最值

对涉及一些求参数范围的恒成立问题时通常采用分离参数，转化为求函数的最值问题。

如函数，函数f(x)在定义域上单调递增，求b的取值范围。

解：内单调递增

∴恒成立

恒成立

令 g(x)=-2x2-2x ∴b≥g(x)max

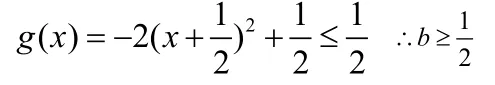
与函数相关的一些恒成立问题最终转化为求函数最值问题，常见的单变量恒成立的几种形式有：

a＞f(x)恒成立；a＜f(x)恒成立

恒成立⇔

成立⇔

二、多项式的最值问题

多项式的最值问题通常有两种基本方法：数形结合（线性规划）；不等式（基本不等式，柯西不等式）。

1．数形结合

对于多项式的最值求法可考查其几何意义结合图像求出其最值。

如：已知经，x,y满足约束条件：

求的取值范围；2、求z=x2+y2的取值范围。

解：（1）由题作出可行域，可看作点(x,y)与点(-5,5) 连线的斜率大小，由图可得

（2）z=x2+y2，可将看作点(x,y)与原点(0,0)的距离。

结合不等式区域A到原点距离最小为

最大为

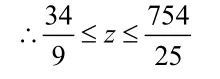
对于此类问题，首先注意将求多项式最值问题转化为几何意义，再运用数形结合的思想求解。

2．应用不等式求解多项式的最值

多项式的最值通常也可应用几个重要不等式，柯西不等式来求解。

这种形式在近三年湖北卷中都有出现，几乎属于必考内容。

如：已知，则的最小值为

解：

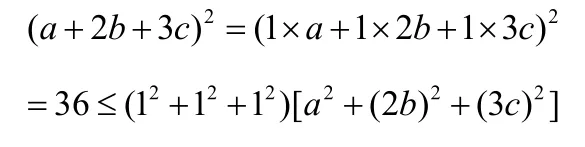
即：

对于一些含有约束条件的多项式的最值问题，一般可以采用柯西不等式处理，配凑构造两组数使之符合柯西不等式的形式，同时要注意符号成立的条件。