最大值指标截尾正态分布精度换算方法*

韩旭，孙翱(.中国人民解放军9550部队，辽宁大连6023；2.中国人民解放军92493部队博士后工作站，辽宁葫芦岛2500)

最大值指标截尾正态分布精度换算方法*

韩旭1，2，孙翱1
(1.中国人民解放军91550部队，辽宁大连116023；
2.中国人民解放军92493部队博士后工作站，辽宁葫芦岛125001)

提出了面向最大值指标的截尾正态分布精度换算方法，为最大值指标与常用精度指标间的精度换算以及真值测量系统精度指标的确定提供了参考依据。该方法假设系统输出序列中各观测点的合格概率服从对数截尾正态分布；根据给定最大值指标的置信水平及序列样本量，证明并推导了截尾正态分布之截尾上限、截尾下限、均值及标准偏差的计算公式，导出了最大值精度指标与1σ等常用精度指标间的换算关系；结合精密仪器有关理论给出了最大值指标下真值测量系统精度指标的确定方法。实例应用的实验结果表明，该方法是可行的。

精度换算；截尾正态分布；最大值指标

现代武器系统对于武器在极端条件下的长期可靠性工作能力要求越来越高，这也对系统的试验、测试实施等提出了更高的要求，以至于有些沿用多年的试验方法、试验理论也必须随之做出调整。最大值指标就是在这样的历史条件下为适应武器实战需求而产生的。文献［1-2］中通过大量的理论研究与实例分析，为最大值指标的实践应用提供了较好的理论支撑。但最大值指标与其他精度指标度量基准间的精度换算仍是一个亟待解决的问题。由最大值指标的定义可知，最大值指标的精度换算问题并不是简单的恒等换算就能解决的。而从科学研究的层面看，各领域中有关此类复杂、非恒定等价换算关系的研究也容易形成热点。例如，在软件工程领域，文献［3］对功能点分析(Function Point Analysis，FPA)及通用软件度量国际协会(COmmon Software Measurement International Consortium，COSMIC)准则之间的功能点估算规模换算问题进行了研究；文献［4-6］则对视频处理领域二维、三维视频标准的数据格式换算问题进行了探讨；而在微处理器电路设计领域，文献［7-8］则对信号处理领域中定、浮点数据间的格式换算问题进行了研究；文献［9-13］也分别针对各自领域生产实践中遇到的坐标变换问题进行了研究。总而言之，尽管人们对于这类复杂、非恒定等价换算关系的研究手段有所不同，但其基本解题思路却是一致的，即采取设定某些约束条件的方法将复杂问题简单化，从而求得有条件的等价换算关系，为特定工程实践提供参考。

1 最大值指标的精度换算

1.1 问题分析

由文献［1］中最大值指标的定义可以看出:在给定的最大值指标H0的条件下，最大值指标之高低由样本区间及其给定的置信水平决定。事实上，样本区间对于最大值指标的影响主要是经由被测系统样本量n来体现的。从而，当给定置信水平1-α时，若被测系统的最大值指标也等于H0，则对于单个样本观测点，其合格概率(即不超过最大值指标H0的概率)应介于区间(1-α，1)内。设对于单个样本观测点i而言，其合格概率为pi∈(1-α，1)，则:

故可做如下假设:设所有样本观测点的对数合格概率都服从均值为n(1-α)的双侧截尾正态分布，其截尾下限A=ln(1-α)，截尾上限B=ln1=0。由于当n＞2时，总有-(1-α)＜(1-α)，且分布的均值点更接近于截尾上限，故该截尾分布为非对称的双侧截尾正态分布。

1.2 原正态分布与截尾正态分布函数关系推导原正态分布与截尾正态分布的主要区别在于其自变量的取值范围不同，原正态分布为(-∞，+∞)，截尾正态分布为［A，B］。假设截尾正态分布的均值及标准偏差分别为μc和σc，原正态分布的均值和标准偏差为μ0和σ0。则由式(3)可得:

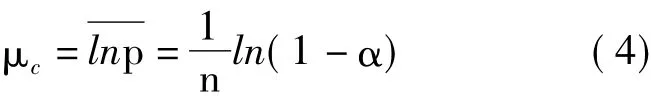
而对原正态分布N(μ0，σ0)而言，其概率密度函数为:

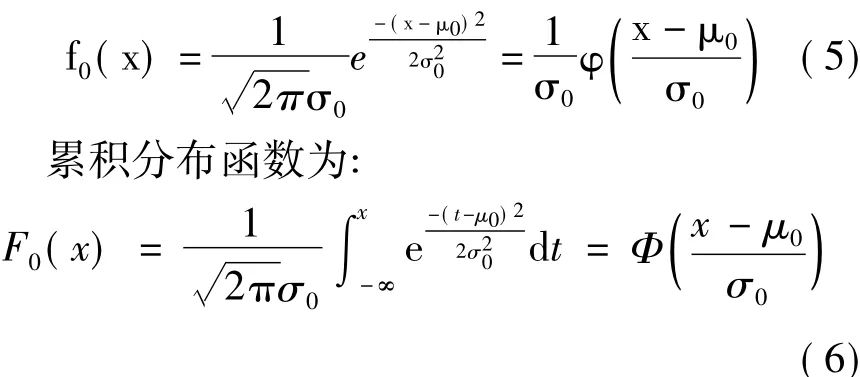
工程实践中，若被试系统工作稳定，其最大值指标下各观测点合格概率也不会差别过大，即分布N(μ0，σ0)的标准偏差σ0变化不大。因此，可假设截尾正态分布的截尾上限B为原正态分布N(μ0，σ0)的3σ分界点，即:

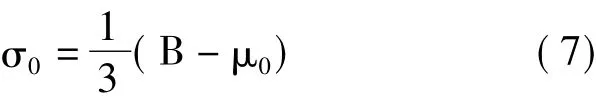
则根据条件概率计算公式，当自变量x∈［A，B］时，截尾正态分布之概率密度函数及累积分布函数分别为:

下面推导原正态分布与截尾正态分布均值及方差的关系。假设原正态分布为N(μ0，σ0)，则截尾正态分布均值:

下面推导截尾正态分布的方差。首先求取截尾正态分布二阶原点矩:

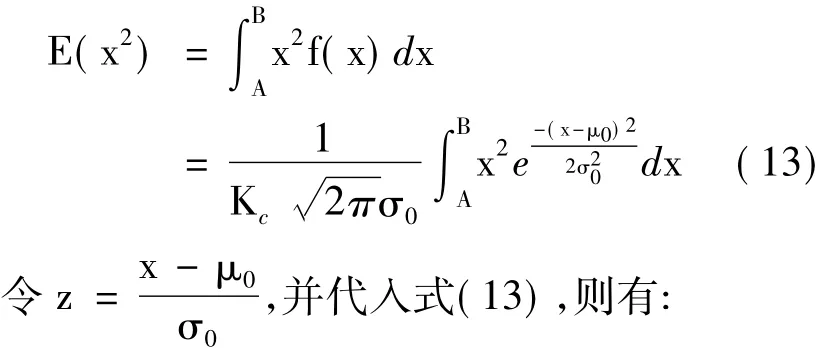
从而求得截尾正态分布的方差为: DX=E(x2)-

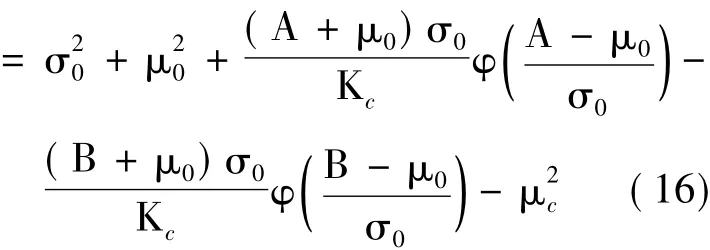
进而得到截尾正态分布标准偏差如式(17)所示:

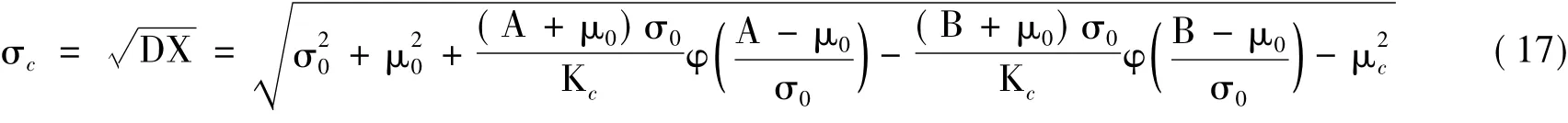
从前面的推导过程看，由式(4)可计算得到截尾正态分布均值μc；由式(7)可得到原正态分布均值μ0与标准偏差σ0的函数解析式；若再能利用截尾正态分布均值μc推导得到μ0，则根据式(17)即可解算出σc，从而得到截尾正态分布的分布函数。

1.3 求解截尾正态分布标准偏差

由于根据式(12)直接由μc求解μ0的函数关系过于复杂，这里以式(12)为依托，使用数值方法求取函数μ0(μc)的近似解。首先验证式(12)中函数的单调性。

将式(7)代入式(12)，有:

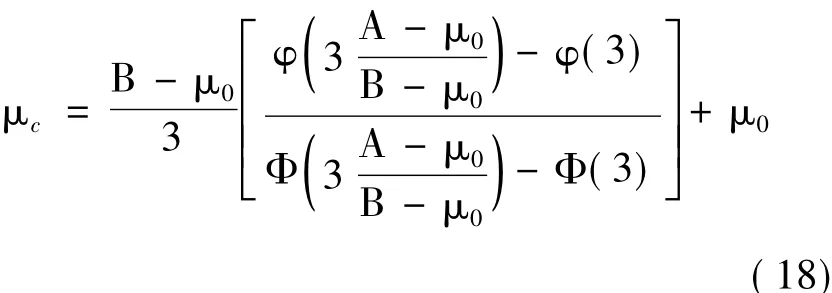
再对式(18)做求导运算，可得:

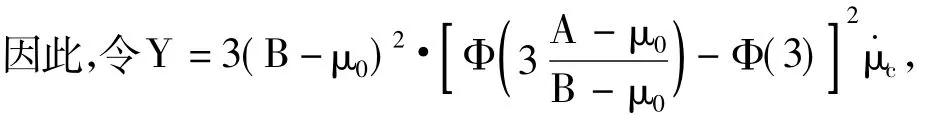
可得:

故总有˙μc＞0，即当μ0∈［A，B］时，函数μc(μ0)是自变量μ0的单调递增函数，可使用数值方法求取函数μ0(μc)的近似解，再将μc，μ0，σ0代入式(17)，即可解算出截尾正态分布的标准偏差σc。数值方法近似求解σc的流程如图1所示。pi下的对数截尾正态分布均值μc及标准偏差σc。故，当取截尾正态分布置信水平为βc时，根据单边正态分布的有关特性，截尾正态分布的分位数:

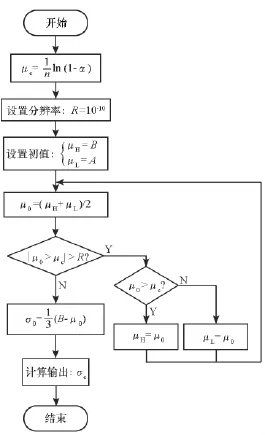
图1 截尾正态分布标准偏差数值求解流程Fig.1 Workflow for approximate solution of standard error under truncated normal distribution

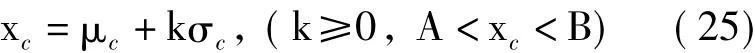
式中，k=Φ-1(βc)。则合格概率分位水平βc下观测点的保精度合格概率:

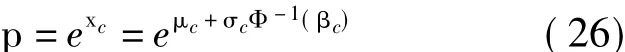
这样，当取最大值指标为H0时，其最大值指标度量基准换算为1σ度量基准下的精度指标为:

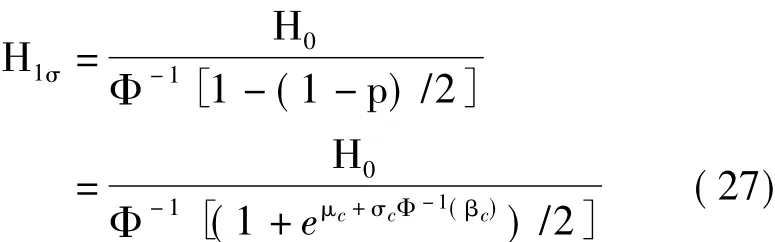
根据式(27)，图2、图3分别给出了给定截尾正态分布置信水平βc=0.5及给定最大值指标置信水平1-α=0.9条件下最大值指标与kσ(k＞0)精度度量基准间的换算关系。

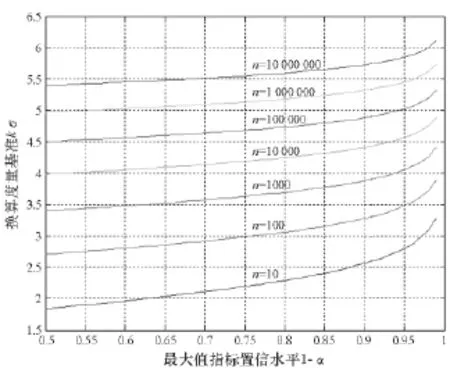
图2 βc=0.5时，最大值指标与kσ基准的换算关系Fig.2 Precision conversion relationship between maximum-error specification and kσ specification whenβc=0.5

由图2、图3可知，当样本量n＞10 000时，最大值指标与kσ度量基准的精度换算主要受样本量n影响，截尾正态分布置信水平βc对精度换算的影响小于10%，而最大值指标置信水平1-α对精度换算的影响也不超过20%。当样本量n＞107时，最大值指标与kσ度量基准的精度换算受样本量n的影响更为显著，截尾正态分布置信水平βc对精度换算的影响小于5%，最大值指标置信水平1-α对精度换算的影响则小于10%。可见，样本量越大，βc，1-α取值对精度换算的影响就越小。当样本量大于10 000时，可忽略βc的影响，此时，若令βc=0.5，则有k==0，则由式(26)、式(4)得p=(1-α)代入式(27)可得大样本量下最大值指标H0换算为1σ度量基准下精度指标:

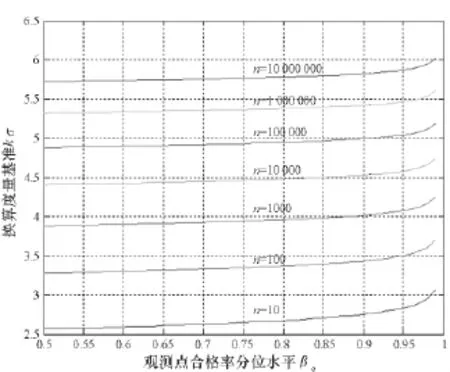
图3 1-α=0.9时，最大值指标与kσ基准的换算关系Fig.3 Precision conversion relationship between maximum-error specification and kσ specification when 1-α=0.9

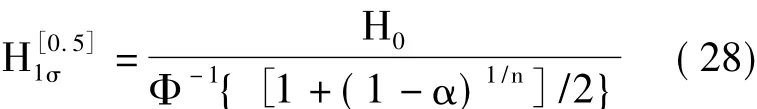
2 真值测量系统精度指标的确定

2.1 常值精度指标的确定方法

真值测量系统精度指标的选定应主要参照精密仪器领域的“1/3法则”或“1/10法则”［14］进行。这样，结合式(27)、式(28)后，即可确定出能够满足最大值指标设备标定的1σ度量基准下真值测量系统的最低精度指标需求。方法如下:

设真值测量系统调节系数为c∈(1/10，1/3)，根据式(28)，大样本条件下，按1σ度量基准统计时，真值测量系统的最低精度指标要求:

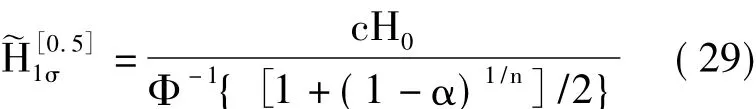
而当样本量不大时，根据式(27)，可按式(30)确定1σ度量基准下的真值测量系统最低精度指标:

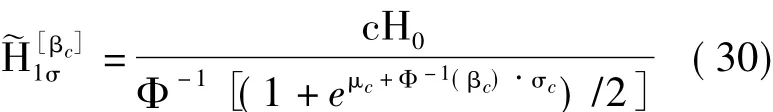
这里要注意，最大值指标条件下的“低精度”在工程实践中可能并非就是低精度。由图2、图3可知，当样本量大于1000时，最大值指标总是高于3σ条件下的相应标准，此时的最大值指标应按照通常意义下的高精度测量标准对待，式(29)、式(30)中调节系数c应参照“1/3法则”取值。真值测量系统精度指标的选择必须综合考查实践成本等现实因素。

2.2 带有时间协变量的精度指标的确定方法

对于带有时间协变量的情形，设协变量序列为Xi，设协变量X与最大值指标H间的函数关系为:

式中:H0为最大值指标的常值部分；f(X)为变值部分，由时间协变量决定。由此，带有时间协变量的最大值指标真值测量系统精度指标可按式(32)确定:

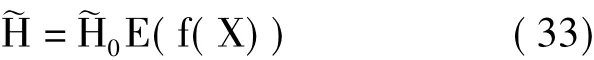
式中，E(f(X))为协变函数f(X)均值。低精度测量中可取:

式中，⌊f(X)」为协变函数f(X)值域下界。

3 应用举例

下面参照美国MK39 MOD3C型激光陀螺惯性导航系统［1］的精度指标，对最大值指标下的真值测量系统精度指标确定方法进行举例说明。

例1假设被测高精度惯导的数据输出频率为100Hz，其240h内的最大值精度指标为:

航向角:7'/cosφ，其中，-85°≤φ≤85°，为载体所在纬度；位置:10海里；线速度:0.6节；纵/横摇角:3'；角速度变化率:0.003°/s。

计算样本量n=240×3600×100=8.64×107≫10 000，属大样本。由式(29)，令α=0.1，βc= 0.5，c=1/3，求得该型惯导的真值测量设备按1σ精度度量基准考量时的最低精度指标分别为:

航向角:23.33″/cosφ；位置:0.55海里；线速度:0.033节；纵/横摇角:10.0″；角速度变化率: 0.6″/s。

例2假设被测低精度惯导数据输出频率为1Hz，其2h内的最大值精度指标如下:

航向角:15'/cosφ，其中，-85°≤φ≤85°，为载体所在纬度；位置:5海里；线速度:1.2节；纵/横摇角:7'；角速度变化率:0.005°/s。

计算样本量n=2×3600×1=7200＜10 000，属小样本。对低精度被试品，可适当增加βc取值，令α=0.1，βc=0.8，则由式(4)可得截尾正态分布均值μc=-1.463 34×10-5。再参照图1流程，由式(12)可用数值方法求解原正态分布的均值μ0=-1.465 5×10-5，将其代入式(7)，可得原正态分布标准偏差σ0=4.885 0× 10-6。再将μc，μ0，σ0代入式(17)可得截尾正态分布的标准偏差σc=4.981 7×10-7。最后，根据式(27)，将α，βc，μc，σc代入后可求得该最大值指标与4.4σ度量基准近似等价，就惯导领域而言，该指标已属高精度指标。故考虑到现实真值测量条件，仍取c=1/3，代入式(30)后，即可求得1σ基准下真值测量系统的最低精度指标:

航向角:1.14'/cosφ；位置:1.36海里；线速度:0.076节；纵/横摇角:31.82″；角速度变化率: 1.36″/s。

当工作于赤道附近(φ=0°)时，协变函数f(X)=⌊f(X)」=1为值域下限。这样，根据式(34)得:其航向角真值测量设备最低精度指标为1.14'。

4 结论

对最大值指标的精度换算问题进行了研究，并以此为基础提出了面向最大值指标的真值测量系统精度指标确定方法，给出了该方法在惯性导航系统真值测量设备精度指标遴选中的应用实例。实验分析及实践应用的结果表明，该方法是可行的。

References)

［1］韩旭，王建宇，祖先锋.基于时间序列模型的系统最大值指标评定方法［J］.系统工程与电子技术，2012，34(4): 839-845.HAN Xu，WANG Jianyu，ZU Xianfeng.System maximumerror specification oriented testing methodology basing on timing series model［J］.Systems Engineering and Electronics，2012，34(4):839-845.(in Chinese)

［2］韩旭，王建宇，祖先锋.基于极值理论的系统最大值指标评定方法［J］.系统工程与电子技术，2012，34(5): 1073-1084.HAN Xu，WANG Jianyu，ZU Xianfeng.System maximumerror specification oriented testing methodology basing on extreme value theory［J］.Systems Engineering and Electronics，2012，34(5):1073-1084.(in Chinese)

［3］Abualkishik A Z，Desharnais J M，Khelifi A，et al.An exploratory study on the accuracy of FPA to COSMIC measurementmethod conversion types［J］.Information and Software Technology，2012，54(11):1250-1264.

［4］Zhang L，Vázquez C，Knorr S.3D-TV content creation: automatic 2D-to-3D video conversion［J］.IEEE Transactions on Broadcasting，2011，57(2):372-383.

［5］Vosters L，de Haan G.Efficient and stable sparse-to-dense conversion for automatic 2-D to 3-D conversion［J］.IEEE Transactions on Circuits and Systems for Video Technology，2013，23(3):373-386.

［6］Yedlin M，Vorst D V，Virieux J.Uniform asymptotic conversion of Helmholtz data from 3D to 2D［J］.Journal of Applied Geophysics，2012，78:2-8.

［7］Liu ZG，Du SY，Yang Y，et al.A fast algorithm for color space conversion and rounding error analysis based on fixedpoint digital signal processors［J］.Computers and Electrical Engineering，2014，40(4):1405-1414.

［8］Menard D，Rocher R，Sentieys O.Analytical fixed-point accuracy evaluation in linear time-invariant systems［J］.IEEE Transactions on Circuits and Systems，2008，55(10): 3197-3208.

［9］Coogle R A，Smith D，Blair W D.Debiased coordinate conversion of bistatic radar measurements［C］//ProcEedings of IEEE National Radar Conference on Ubiquitous Radar，Atlanta，GA，United States，2012:383-388.

［10］Zhang R F，Zhang X M，Qin G X，et al.Novel threedimensional data conversion technique and profile measurement system for engine cylinder head blank［J］.Optics＆Laser Technology，2013，45:697-701.

［11］Bernhard HW，Herbert L，ElmarW.GNSS-globalnavigation satellite systems:GPS，GLONASS，Galileo，and more［M］.USA:SpringerWien NewYork，2008.

［12］Williams C E.A comparison of circular error probable estimators for small samples［D］.USA:Air Force Institute of Technology，1997.

［13］Zelenkov A，Kluga A，Grab E.Accuracy estimation of GPS receiver parameters with re-reference system in static mode［J］.Telecommunications and Electronics，2008，88 (80):31-36.

［14］Auromotive Industry Action Group.Measurement systems analysis reference manual［M］.4th ed.USA:Auromotive Industry Action Group，2010.

Precision conversion methodology w ith truncated normal distribution theory assumption oriented to maximum-error specification

HAN Xu1，2，SUN Ao1
(1.The PLA Unit91550，Dalian 116023，China；2.PostdoctoralWorkstation of the PLA Unit92493，Huludao 125001，China)

A precision conversionmethodology with truncated normal distribution theory assumption oriented tomaximum-error specification was brought forward，and it could be taken as a reference frame for the precision conversion between maximum-error specification and other precision measurement specifications，so that the precision class of according true valuemeasurement systems could be determined in advance.Themethod assumes that the conformity probability of the observation sequence is subjected to logarithmic truncated normal distribution；based on the aimed confidence level formaximum-error specification and the given sample size of target sequence，the calculation formulation of upper truncated limit，lower truncated limit，mean and standard deviation of the truncated normal distribution were proved and derived，thus the precision conversion relationships between maximum-error specification and other precisionmeasurement specifications，such as 1σ，were turned out；through referring to the corresponding theories on precision instrument fields，the determination methodology for precision class of true valuemeasurement systems undermaximum-error specification was given.The application on related example cases proved the feasibility of the proposed method.

precision conversion；truncated normal distribution；maximum-error specification

N94

A

1001-2486(2015)05-110-06

10.11887/j.cn.201505017

http://journal.nudt.edu.cn

2014-11-14

教育部博士点新教师基金资助项目(200802881012)

韩旭(1975—)，男，辽宁开原人，工程师，博士，E-mail:china_hanxu@163.com