单像自标定的迭代优化方法*

刘丹，刘学军，2，王美珍，2(.南京师范大学虚拟地理环境教育部重点实验室，江苏南京20023；2.警用地理信息技术公安部重点实验室，江苏常州23022)

单像自标定的迭代优化方法*

刘丹1，刘学军1，2，王美珍1，2
(1.南京师范大学虚拟地理环境教育部重点实验室，江苏南京210023；2.警用地理信息技术公安部重点实验室，江苏常州213022)

针对基于灭点的单像自标定方法精度不高的局限性，利用影像中的灭点和椭圆几何约束信息，提出一种迭代优化的单像自标定方法。根据极点-极线关系及其表示的正交性，由影像中的椭圆曲线及其所在平面的灭线确定一组正交共轭灭点对。利用这些正交共轭灭点对建立关于主距和主点的非线性模型，以主距的方差最小作为优化准则，并选用多个位置作为主点的初始值进行多次迭代优化估计，获得主距和主点的最优结果。仿真影像和真实影像实验结果表明，该方法能够有效地实现单像自标定。与基于灭点的摄像机标定方法相比，该方法能够获得更为满意的标定结果。

摄像机标定；灭点；椭圆；迭代优化

摄像机标定是摄影测量和计算机视觉领域中的基本任务之一，其目的是从摄像机摄取的二维影像出发，计算摄像机的内外参数，并由此重构三维场景。传统的摄像机标定方法［1-3］利用已知的标定物进行标定，标定精度高，但需要事先已知标定物，适用性受限。近年来，利用影像信息进行标定的摄像机自标定方法引起了研究者们广泛的兴趣，并对其进行了大量的研究。传统的自标定方法需要场景的两幅或者两幅以上影像，利用影像之间对应的特征点关系进行标定［4-6］，而基于单幅影像的自标定方法由于缺乏影像之间的对应关系，只能利用影像中的几何特征进行标定，主要包括基于灭点/灭线［7-8］、基于圆形［9-10］、基于对称性［11］和基于共面点/共面性［12-13］的标定方法。

随着数码相机应用的深入普及，基于灭点的单像自标定方法受到了研究学者们的高度重视。Caprile等［7］首次提出利用三个灭点进行标定，采用45°角拍摄的立方体影像作为标定物。随后，众多学者在此基础上进行了研究。Guillou等［8］利用单幅影像中的两个灭点和一条已知线段进行标定；张祖勋等［14］利用灭点与方位元素之间的几何关系，建立灭点平差模型，通过迭代求解内外方位元素；霍炬等［15］利用两组正交的平行直线形成的灭点信息，并加入畸变系数进行非线性优化。但是基于灭点的标定方法仍然存在一些不足:灭点易受噪声的影响，使得基于灭点的标定方法精度不高，尤其是难以精确地估计主点的位置；当影像中只存在两个正交方向的灭点时，需假设主点坐标已知(如位于影像中心)，而这不符合实际条件，因此利用灭点通常只能进行弱标定。

自然场景中不仅含有大量的直线信息，还含有许多圆形物体，如井盖、标志牌等。因此，结合场景中的直线和圆形等信息，提出一种摄像机内参的迭代优化方法。在基于灭点的摄像机标定基础上，根据极点-极线关系及其表示的正交性，进一步进行迭代优化，获取主距和主点坐标的最优解。

1 原理与方法

1.1 基于灭点的摄像机标定方法

空间上一组平行直线，在影像上会聚焦于一点，即灭点。基于灭点的标定方法就是利用透视变换下灭点的正交性进行标定，其原理为:空间上三组正交的平行线投影在影像上的直线段分别聚焦于三个灭点，其在摄像机坐标系下仍然正交［4］。因此，当场景满足“Manhattan World Assumption”(即场景中存在三个相互正交方向(称为主方向)的直线)时，就可以利用三个正交方向的灭点标定三参数模型:主距f和主点坐标(x0，y0)；若场景中只存在两个正交方向的直线，则需假设主点坐标已知(通常假设位于影像中心)，且只能标定一参数模型，即主距f。f可以由主点坐标和任意一对正交灭点计算得到:

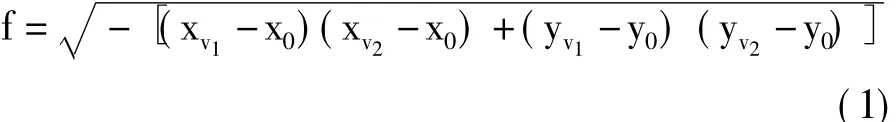
式中，(xv1，yv1)，(xv2，yv2)为两个正交灭点v1，v2的坐标。

灭点对噪声非常敏感，使得基于灭点的摄像机标定方法标定精度较弱，尤其是对主点位置的计算不稳定；此外，基于灭点的标定方法对场景的限制比较大，需要场景满足“Manhattan World Assumption”条件，而当只存在两个正交方向的直线时，则只能标定一参数模型。因此，利用灭点进行单像标定通常是对摄像机进行弱标定。

1.2 基于迭代优化的单像标定方法

结合影像中的灭点和椭圆二次曲线信息，根据极点-极线关系及其表示的正交性，对相机主距和主点坐标进行迭代优化。

1.2.1 正交共轭灭点对

极点-极线关系:设x为平面上的一点，C为平面上的一条二次曲线，则点x和二次曲线C能够定义一条直线l=Cx。这条直线l=Cx就称为x关于C的极线，而点x=C-1l称为l关于C的极点［3］。极线l上的任意一点y与极点x关于二次曲线C共轭，且满足yTCx=0。如图1(a)所示。

由极点-极线关系表示的正交性:设C为平面内的一条二次曲线，v1，v2分别为两个不同直线方向所对应的灭点，若这两个直线方向正交，则灭点v1，v2关于二次曲线C共轭，满足vT2Cv1=0［16］。此时v1，v2称为正交共轭灭点对。同样，若平面内两个灭点v1，v2满足vT2Cv1=0，则这两个点所对应的直线方向相互正交。

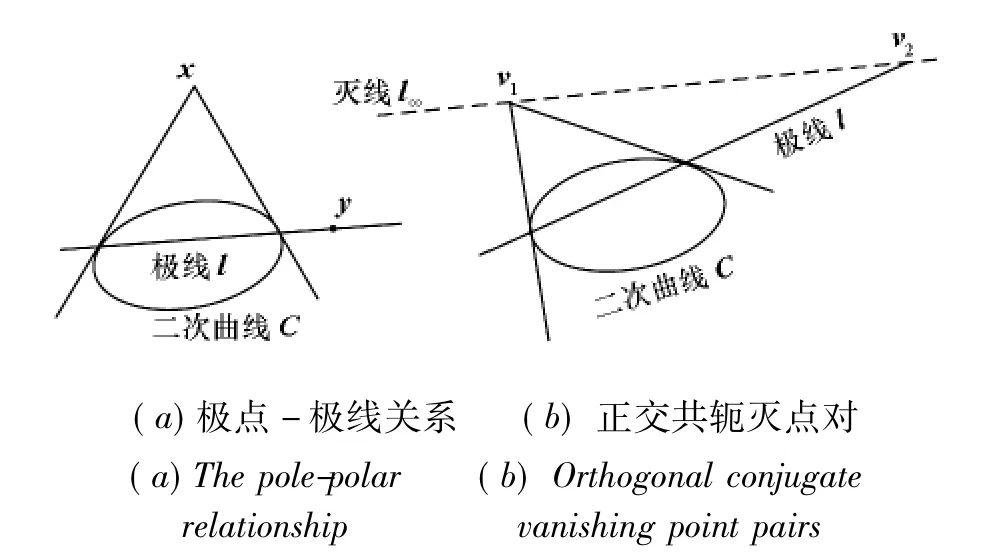
图1 极点-极线关系表示的正交共轭灭点对Fig.1 Orthogonal conjugate vanishing point pairs computed by the pole-polar relationship

如图1(b)所示，l∞为平面内的灭线，C为二次曲线。l∞上的点v1和直线l是关于二次曲线C的极点-极线关系，即l=Cv1。灭线l∞和极线l交于一点v2。根据极点-极线关系及其表示的正交性可知，v1和v2关于二次曲线C共轭，并且是一对正交共轭灭点，满足vT2l=vT2Cv1=0。因此，给定平面内一条灭线l∞和绝对二次曲线C，灭线l∞的任意一点v1的正交共轭灭点是v1关于C的极线l和灭线l∞的交点，即可通过式(2)计算v1的正交共轭灭点v2。

因此，若已知平面内的一条二次曲线(如椭圆)及该平面的灭线时，可以根据式(2)得到一组正交共轭灭点对。

1.2.2 迭代优化进行标定

当主点坐标已知时，利用一对正交共轭灭点根据式(1)就可以计算主距f。但由式(2)可以得到n对正交共轭灭点，并且每对正交共轭灭点计算的主距值不同，由此便得到了一组主距F={f1，f2，…，fn}。根据主距的计算公式(1)可知，主距f的值与灭点对和主点有关。在采样点(即n对正交灭点)不变时，计算得到的一组主距F的误差与主点误差相关，主点坐标越靠近真实值，F中的所有主距值分布越集中，相反，主点位置越偏离真实值，F的分布越分散。由于方差是衡量取值分散程度的一个尺度，因此可以用F的方差D作为评价准则判断主点位置的正确性，方差D越小，主点的值越接近真实值。当主点的位置正确时，D应该最小。利用方差D作为目标函数，对主点坐标(x0，y0)和主距f进行迭代优化:

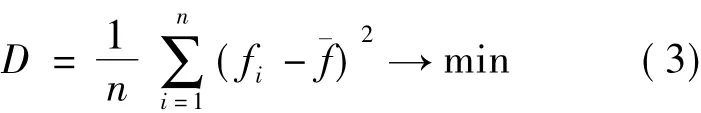
式中，fi是由第i对正交灭点(i=1，2，…，n)通过式(1)计算得到的主距，¯f为F的均值。

式(3)是一个参数为(f，x0，y0)的非线性模型，利用Levenberg-Marquardt(LM)算法进行迭代优化求解。为解决LM算法的初值选取和存在陷入局部极小值的问题，在优化过程中选用多个点(如以影像中心为中心的100×100的窗口)作为主点的初始值，对于每个初始值利用式(3)进行迭代优化得到多个优化结果，选择其中方差最小的结果作为最终的优化结果。算法的具体流程如图2所示。

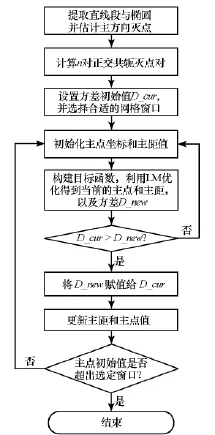
图2 基于迭代优化的单像自标定Fig.2 Camera self-calibration from a single image based on iterative optimization

2 实验与分析

通过仿真影像和真实影像实验对所提方法进行验证，在实验中，与基于灭点的摄像机标定方法［7］进行对比，由此验证所提方法的可行性及有效性。

2.1 仿真实验

仿真实验数据为在三维空间上生成的三个正交方向的直线和一个圆，如图3(a)所示，每个方向生成11条直线。仿真采用主距为15mm，像素大小为0.0067(mm/pixel)的模拟摄像机，影像大小设置为1280×1024(pixel×pixel)。使用以上摄像机参数将生成的空间数据投影到二维平面上，得到的透视投影影像如图3(b)所示。

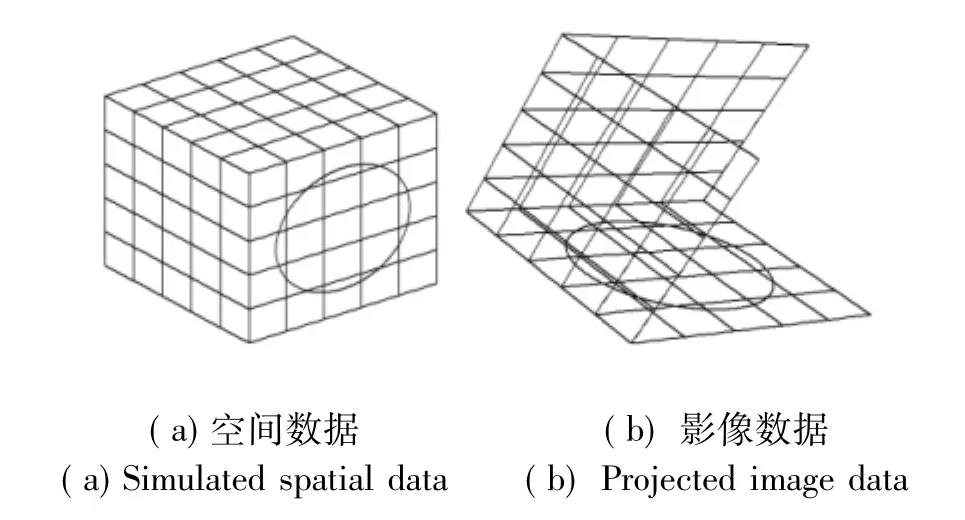
图3 仿真实验数据Fig.3 Data of simulated experiments

实验中分别将主点坐标向左和向上偏移(10，10)，(20，20)，(50，50)，得到主点坐标不同的三组数据(设为c=(10，10)，(20，20)，(50，50))。为分析噪声对结果的影响，对每组数据的每个影像点分别加上均值为0，均方差为δ=0，0.2，0.4，…，4的高斯噪声。基于灭点的标定方法和本文方法得到的标定结果如图4所示。图4(a)分别为三组数据使用两种方法计算的主点坐标在不同噪声水平下的偏移量(绝对误差)，图4(b)分别为三组数据使用两种方法计算的主距在不同噪声水平下的相对误差，图中VP表示基于灭点的摄像机标定方法，Pro表示本文方法。

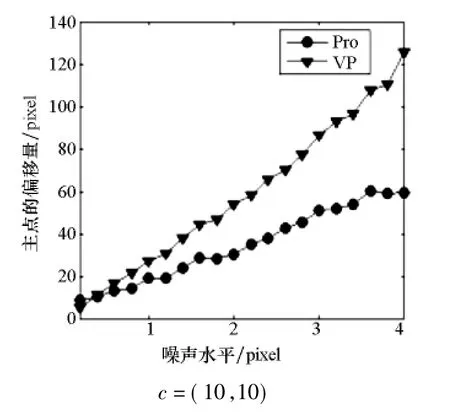
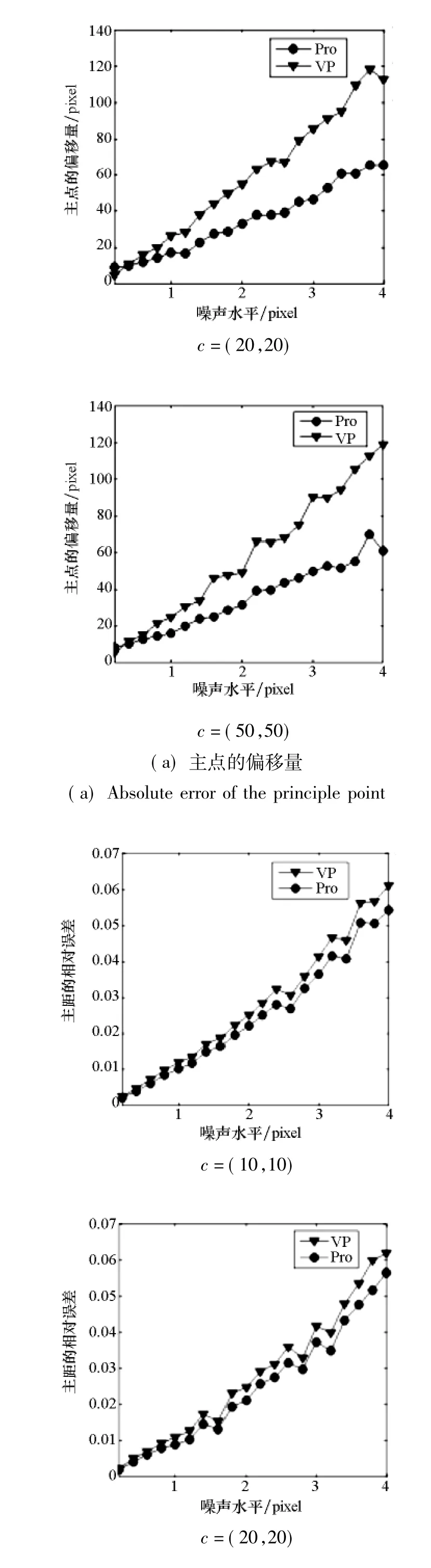
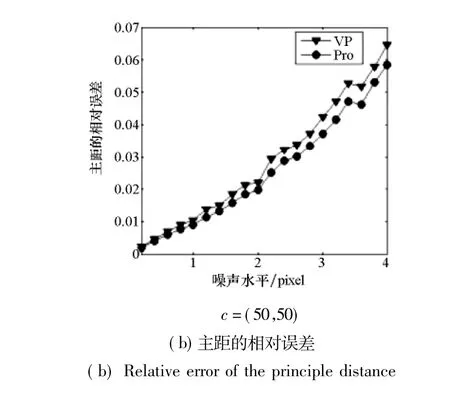
图4 仿真实验结果Fig.4 Results of simulated experiments

2.2 真实影像实验

2.2.1 实验数据

真实影像实验采用不同型号的摄像机拍摄得到场景影像，然后对其进行实验与分析，采集的实验数据如表1所示，拍摄的影像数据如图5所示。在实验中，首先采用直线段检测器(Line Segment Detection，LSD)［17］提取影像中的直线段，使用多模型稳健估计(J-Linkage)［18］对提取的直线段聚类分组，采用直接最小二乘方法［19］拟合影像中的椭圆；然后根据分组得到的直线段，利用奇异值分解(Singular Value Decomposition，SVD)解算三个/两个主方向的灭点坐标。图5中显示的是直线段检测与聚类后三个主方向的直线段以及椭圆拟合后得到的结果。

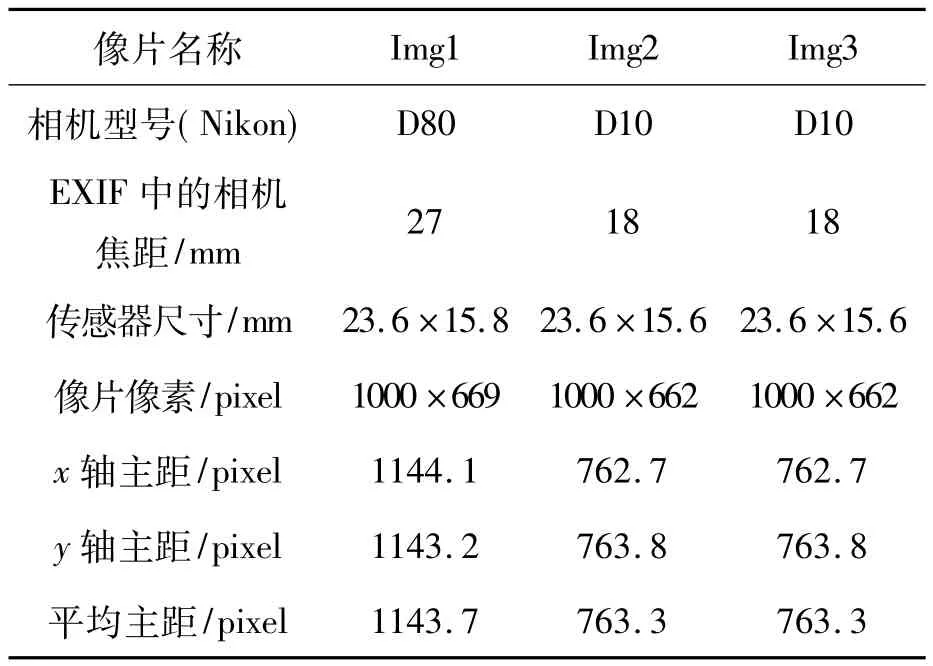
表1 真实场景实验数据Tab.1 Experiment data of real scenario

2.2.2 实验结果

采用上述实验数据，分别利用本文提出的方法和基于灭点的方法计算标定参数，两种方法的实验结果如表2所示。从表2可以看出本文方法的标定精度相对于基于灭点的单像自标定方法有所提高。

图5 实验影像Fig.5 Experimental images

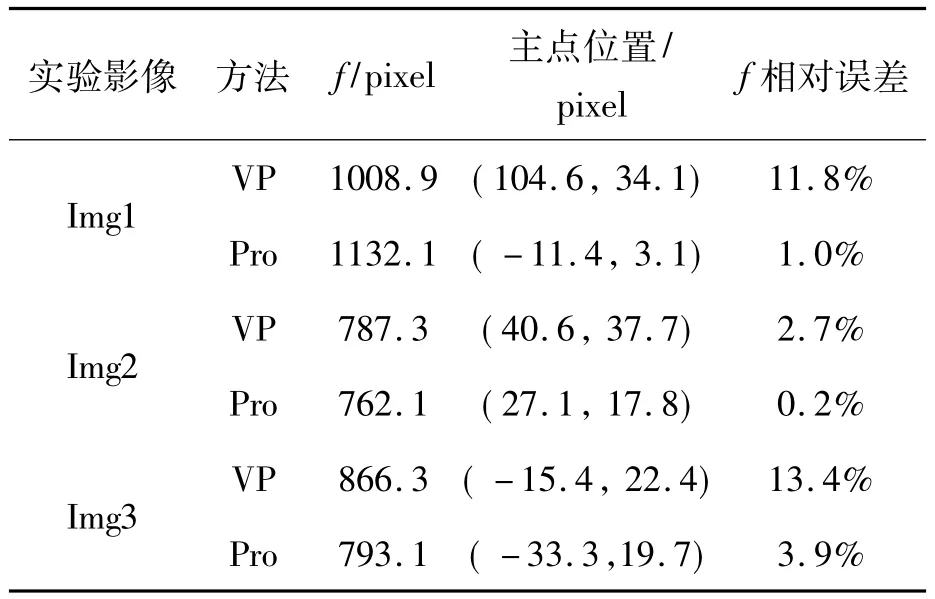
表2 两种方法的摄像机标定结果Tab.2 Results of camera calibration estimated by the twomethods

2.3 分析与讨论

基于迭代优化的单像自标定方法，利用场景中的圆形物，对标定参数进行迭代优化。对仿真实验和真实影像实验结果进行分析:①从仿真实验结果图4中可以看出，主点坐标的求解易受噪声的影响，进一步影响了主距的精度，在经过迭代优化后，主点的精度有了较大的提高，进一步使得主距的求解更加精确；在真实实验结果表2中，对于三组实验数据，基于灭点的摄像机标定方法得到主距的相对误差分别为11.8%，2.7%，13.4%，而基于本文方法标定的主距的相对误差分别为1.0%，0.2%，3.9%，可以看出本文方法的标定精度相对于基于灭点的方法有较大的提高。②真实影像实验中利用影像Img1进行摄像机标定时，由于提取的直线段中含有较多错误分类线段，导致基于灭点的摄像机标定精度较差，但是通过迭代优化后的结果有较大的提高。③真实影像实验中后两者实验影像的实验数据相同，但是基于影像Img2的标定精度高于基于影像Img3的标定精度，这是由于场景影像Img3中只富含两个方向的直线信息，第三个方向的直线非常少，从而使得该方向估计的灭点误差非常大，直接影响了摄像机标定结果，但是通过迭代优化后的标定精度有所提高。

根据以上实验分析可知，本文方法充分利用了影像中的灭点和椭圆二次曲线几何约束条件，对标定参数进行迭代优化求解，与基于灭点的单像标定方法相比，本文方法能够有效地提高摄像机标定的精度。利用基于灭点的摄像机标定方法需要场景满足“Manhattan World Assumption”条件，当场景中只含两个主方向的直线时，其标定结果不够理想，但是本文方法结合椭圆信息进行迭代求解，能够较好地提高标定精度，因此，相对于基于灭点的摄像机标定方法，本文方法能够适当放宽对场景的约束。

3 结论

基于极点-极线关系及其表示的正交性，提出了一种基于迭代优化的单像自标定方法，并通过仿真和真实数据实验对该方法进行了验证与分析。方法充分利用了影像中的灭点和椭圆几何信息，对基于灭点的摄像机标定进行改进，对场景进行多约束标定。实验结果表明，与基于灭点的摄像机标定方法相比，迭代优化方法的标定精度较高。由于灭点误差影响摄像机标定精度，而灭点易受噪声的影响，仅利用灭点进行摄像机标定，难以保证摄像机标定精度。场景中存在很多几何特征，因此，为进一步提高摄像机标定结果的精度和稳定性，下一步将研究如何加入更多的几何约束条件进行摄像机标定。

References)

［1］Abdel-Aziz Y I，Karara H M.Direct linear transformation from comparator coordinates into object space coordinate in close-range photogrammetry［C］//Proceedings of Symposium on Close-Range Photogrammetry，Falls Church，VA: American Society of Photogrammetry，1971，1:1-18.

［2］邱志强，唐力铁，于起峰.用神经网络变易有效焦距的摄像机标定法［J］.国防科技大学学报，2002，24(5):16-19.QIU Zhiqiang，TANG Litie，YUQifeng.A camera calibration method of varying effective focal length by neural network［J］.Journal of National University of Defense Technology，2002，24(5):16-19.(in Chinese)

［3］唐力铁，邱志强，陆启生.基于仿射近似的摄像机标定［J］.国防科技大学学报，2006，28(1):111-116.TANG Litie，QIU Zhiqiang，LU Qisheng.Camera calibration based on affine approach［J］.Journal of National University of Defense Technology，2006，28(1):111-116.(in Chinese)

［4］Tsai R Y.A versatile camera calibration technique for high-accuracy 3D machine vision metrology using off-the-shelf TV cameras and lenses［J］.IEEE Journal of Robotics and Automation，1987，3(4):323-344.

［5］Zhang Z Y.A flexible new technique for camera calibration［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2000，22(11):1330-1334.

［6］Hartly R，Zisserman A.Multiple view geometry in computer vision［M］.USA:Cambridge University Press，2000.

［7］Caprile B，Torre V.Using vanishing points for camera calibration［J］.International Journal of Computer Vision，1990，4(2):127-139.

［8］Guillou E，Meneveaux D，Maisel E，et al.Using vanishing points for camera calibration and coarse 3D reconstruction from a single image［J］.The Visual Computer，2000，16(7):396-410.

［9］Chen Q，Wu H Y，Wada T.Camera calibration with two arbitrary coplanar circles［C］//Proceedings of8th European Conference on Computer Vision，Prague，Czech Republic: Springer Berlin Heidelberg，2004，3023:521-532.

［10］Colombo C，Comanducci D，Del Bimbo A.Camera calibration with two arbitrary coaxial circles［C］// Proceedings of9th European Conference on Computer Vision，Graz，Austria:Springer Berlin Heidelberg，2006，3951: 265-276.

［11］Hong W，Yang A Y，Huang K，et al.On symmetry and multiple-view geometry:structure，pose，and calibration from a single image［J］.International Journal of Computer Vision，2004，60(3):241-265.

［12］Shang Y，Yu Q F，Zhang X H.Analyticalmethod for camera calibration from a single image with four coplanar control lines［J］.Applied Optics，2004，43(28):5364-5369.

［13］Park J.Quaternion-based camera calibration and 3D scene reconstruction［C］//Proceedings of Computer Graphics，Imaging and Visualisation，2007:89-92.

［14］张祖勋，吴军，张剑清.建筑场景三维重建中影像方位元素的获取方法［J］.武汉大学学报·信息科学版，2003，28(3):265-271.ZHANG Zuxun，WU Jun，ZHANG Jianqing.A method for determining drientation parameters in image-based reconstruction of architectural scenes［J］.Geomatics and Information Science of Wuhan University，2003，28(3): 265-271.(in Chinese)

［15］霍炬，杨卫，杨明.基于消隐点几何特性的摄像机自标定方法［J］.光学学报，2010，30(2):465-472.HUO Ju，YANG Wei，YANG Ming.A self-calibration technique based on the geometry property of the vanishing point［J］.Acta Optical Sinica，2010，30(2):465-472.(in Chinese)

［16］Semple J G，Kneebone G T.Algebraic Projective Geometry［M］.UK:Clarendon Press，1998.

［17］von Gioi R G，Jakubowicz J，Morel J-M，et al.LSD:a fast line segment detector with a false detection control［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2010，32(4):722-732.

［18］Toldo R，Fusiello A.Robust multiple structures estimation with J-Linkage［C］//Proceedings of 10th European Conference on Computer Vision，Marseille，France:Springer，2008，5302:537-547.

［19］Halir R，Flusser J.Numerically stable direct least squares fitting of ellipses［C］//Proceedings of the 6th International Conference in Central Europe on Computer Graphics and Visualization，Plzen，Czech Republic，1998，125-132.

Iterative optim ization for camera self-calibration from a single image

LIU Dan1，LIU Xuejun1，2，WANGMeizhen1，2
(1.Key Laboratory of Virtual Geographic Environment Ministry of Education，Nanjing Normal University，Nanjing 210023，China；2.Key Laboratory of Police Geographic Information Technology Ministry of Public Security，Changzhou 213022，China)

The camera calibration from vanishing points is easily distracted by noise in the image，leading to inaccurate resultswhich are often inadmissible for camera calibration.To overcome the limitation，an iterative optimization approach，whichmakes full use of geometric constraints of vanishing points and ellipse in the image，was presented for self-calibration from single image.According to the pole-polar relationship and the orthogonality represented by it，a set of orthogonal conjugate vanishing point pairswere calculated through using the ellipse curve and the coplanar vanishing line.A nonlinearmodel of the principle distance and principle pointwas established on the basis of these vanishing point pairs.Choosing theminimum variance of principle distances as optimization criterion and setting multiple points as the initial values of the principle point，the principle distance and principle pointwere iteratively optimized and their optimal results were obtained.Simulated results and real data show that the approach can effectively realize camera self-calibration from a single image.Compared with the camera calibration method using vanishing points，the approach achievesmore satisfactory calibration results.

camera calibration；vanishing points；ellipse；iterative optimization

TP391

A

1001-2486(2015)05-029-06

10.11887/j.cn.201505005

http://journal.nudt.edu.cn

2014-12-04

国家自然科学基金资助项目(41401442)；“十二五”国家支撑计划资助项目(2012BAH35B02)；江苏省普通高校研究生科研创新计划资助项目(KYLX15_0748)

刘丹(1989—)，女，江西抚州人，博士研究生，E-mail:demondan@163.com；刘学军(通信作者)，男，教授，博士，博士生导师，E-mail:liuxuejun@njnu.edu.cn