以形辅数话向量

☉江苏省海门中学 王 娟

以形辅数话向量

☉江苏省海门中学 王 娟

向量是新课程中学数学的重要内容，其对思维的考查要求相比以往陈旧的数学知识来得更为灵活，更容易成为编制出优秀试题对学生能力分层的重要知识章节.北师大张英伯教授非常推崇向量，早在2000年时就力荐将向量内容移植到高中数学内容中，在新课程2003年开始实施后向量章节终于出现在必修4中.为什么向量如此受重视呢？我们可以借鉴数学家吴文俊先生的话语：“向量并不是一个纯粹的单一知识章节，它是一种问题解决的工具，在解决几何问题的过程中，向量将问题可以代数化，进而演变成机械化的证明，这是向量的一种极为重要的作用.”其实我们感受到向量机械化证明的内容体现在向量的坐标化运用和空间几何的向量法使用.

一方面，向量不仅用其代数方式解决了很多比较困难的几何问题；另一方面也大大体现了价值，恰是其图形化的工具性作用.向量图形化的使用策略，将原本较为复杂的问题以向量几何图形的方式将其展示出来，其几何意义跃然纸上，问题的解决显得较为轻松.笔者认为，中学数学的向量问题主要是两种方式，即向量的代数化运算（坐标化运算是其特殊情形）和向量的图形化策略，哪种方式对于思维的启发和促动更大呢？显然是图形化的策略，即以形辅数.代数化方式在解决问题时对于思维的考查作用不如图形化策略明显，因此在中学向量知识环节中代数化并未达到吴文俊先生说的机械化的地步.通过图形化使用方式，我们来看看如何解决向量问题的以形辅数.

一、构造三角形

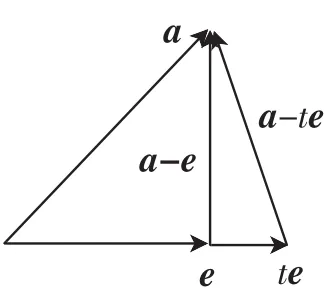
图1

例1已知向量a≠e，|e|=1，对任意t∈R，恒有|ate|≥|a-e|，则下列命题正确的是_________.

（1）a⊥e；（2）a⊥（a-e）；

（3）e⊥（a-e）；（4）（a+e）⊥（a-e）.

解析：本题改编自浙江高考试题，可以采用代数化的方式，对其进行以t为自变量的二次函数分析，利用判别式解决问题，有兴趣的读者可以试试，在处理Δ≤0得到（a·b）2时要提醒学生注意（a· b）2≠a2·b2，这是代数化解决的关键；但是笔者思考，这样的问题若使用图形化方式更能凸显向量解决问题的本质，因此以形辅数才是这种问题更直接的反映：如图1，建构向量e和向量a，利用向量减法可得a-e，任意选择te，利用向量减法可得a-te，对任意t∈R，要使得|a-te|≥|a-e|成立，则显然（a-e）所在线段为垂线段，即e⊥（a-e）.从图形化策略中，我们发现问题的解决显得异常轻松，其为何|a-e|最短的本质跃然纸上，这正是向量图形化功能的正确使用.

图2

解析：与例1类似，本题也是采用向量三角形正确构造下的图形化策略.不妨令观察图2，可知线段AC为垂线段，故△ABC为直角三角形.

图3

变式2：△ABC所在的平面记为α，平面α内一点P与平面外一点M，满足对任意的x，y∈R则异面直线PM与BC所成的角为___________.

说明：上述问题都是以三角形知识进行建构，将向量加减法的三角形法则运用到实际问题中，是构建图形的关键.笔者也发现，学生对于三角形法则不可谓不熟悉，但是在解决实际问题的时候，往往却一筹莫展，对于图形化的建构，笔者认为学生不善于利用的主要原因是：第一，运用思维还是运用运算，学生的第一选择往往是宁可计算也不愿思考，这是因为向量机械化给出了方向，但是令一般学生望而生畏的运算往往是问题解决的障碍；第二，数形结合思想的缺失，导致学生解决向量问题往往不会构图、不想构图，或者是对构图没有正确掌握其最核心的条件，上述三个问题都围绕同一个想法，即垂线段最短，这体现出向量在其他知识交汇处的考查值得教师继续研究.

二、构造圆

解析：如图4所示，向量a，b满足夹角120°，且a-c与b-c的夹角是60°，这里可分两种情况，一是A，B，C在以O为圆心，半径为1的圆上，此时|c|=1；二是以四点共圆来建构图形.设∠AOB=120°，∠ACB=60°，可知点C的轨迹是优弧一动点，显然当点C为优弧的中点时，取到最大值，即为O，A，B，C四点所在圆的直径.易得在△ABC中，由正弦定理得

图4

图5

变式：已知向量a，b满足|a|=|b|=a·b=2，且（a-c）·（b-2c）=0，则|b-c|最大值为_________.

解析：如图5所示，若对条件分析可知，向量a，b满足夹角60°，而（a-c）·（b-2c）=（a-c）这样问题就围绕向量a，b，c建构图形解决.设，D为线段OB中点，则由题意可知（a-c）即∠ACD=90°，可知点C的轨迹是以Q为圆心，以AD为直径的圆上的点.又问题转化为定点B与圆上动点C的最值.至此，问题已到达学生能认知的模式，|b-c|的最大值为BQ+r.给出计算：半径，所以|b-c|max=

说明：构造圆形解决向量问题，是利用了特定的平面几何中的相关知识，诸如对角互补的四点共圆、动态三角形直角顶点必定落在某一圆的边界上.这种以形辅数解决向量问题，显然较第一种构造难度更大，笔者认为首先认知题中所涉及的向量条件是第一步，将条件选择成图形的建构是难点，需要教师合理的引导和阐述，最后问题转变为与圆上动点相关的问题，利用平面几何知识可知，往往与圆心的距离有关.

三、自由向量的构造

向量章节从2003年进入高中数学新课标之后，笔者越来越感受到它的无穷魅力.其不受任何约束的建构和使用，成为解决问题最自然的一种武器.那么，向量章节中最核心的知识体现在哪个知识点上呢？很多教师在不断教学生演算坐标化下的向量、解决数量积的熟练程度，这些是基本功，但是没有触及向量的核心，笔者以为向量核心知识是平面向量基本定理.这个基本定理的良好理解，才能真正深刻认识后续向量正交分解的坐标化只不过是其特殊情形而已.

自由化坐标的建立：如图6所示，三点A，Q，B共线，则存在实数x，y，使得若以x，y作为有序点对（x，y），以为各自一个单位，OA→x轴，OB→y轴，建立斜角坐标系，类比直角坐标系下坐标的性质，可以得到如下延伸：

图6

（1）过点O且平行于AB的直线，其斜角坐标系下方程为：x+y=0；

（2）以OA为x轴，OB为y轴建立的斜角坐标系也分为四个象限，类比直角坐标系下线性规划知识可得自由化坐标下的线性规划，如下文中1-1区域指的是第一象限1号区域，其余类似.

例3Rt△ABC中，AB为斜边，BC=2，正△BCD满足AB⊥BD，P在等边△BCD内部（含边界）运动，记E为AB的中点，若则λ+μ的取值范围是_________.

分析1：笔者自编了本题，主要是考查学生是否可以利用图形化的策略将问题构建成自由坐标的方式解决.查看学生的解决过程，笔者发现大多数学生首先想到的是下面的方式.

图7

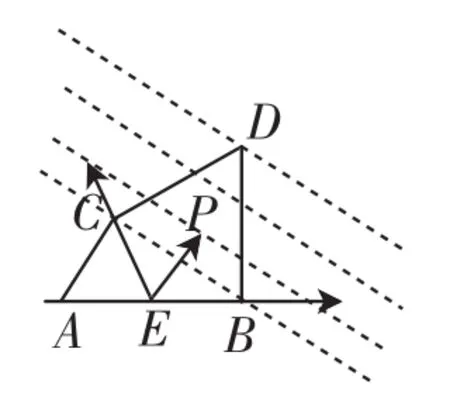
图8

解法1：如图7所示，以B为原点，AB、BD所在的直线分别为x轴、y轴建立直角坐标系，则B（0，0），D（0，2），

解法2：如图8所示，用自由向量建构的坐标系，以E为原点，EB为λ轴，EC为μ轴建系.

说明：灵活运用向量图形化的建构策略，是将平面向量基本定理学习到精髓的体现.平面向量基本定理是向量知识的重中之重，可惜的是，当下的向量教学却过多地涉及了向量的代数化，将无限可能的自由化分解抛诸脑后.从上述笔者自编的问题可以看出，学生依旧对于正交分解情有独钟，但是较为烦琐的运算却恰恰限制了向量优越性的体现，而以自由化坐标体现的方式恰恰将平面向量基本定理的精髓呈现出来，我们可以清楚地看到三点共线性质使用后，利用平行线的等间距性质，轻松地解决自由化坐标下的横坐标与纵坐标的类线性规划问题，其思维更高端、更前瞻、更美妙，这才是向量思维性的价值体现.

总之，中学数学的向量教学一直是两条途径的教学.代数化和图形化始终围绕着向量教学的始终，从近几年越来越频繁的考查来看，向量试题的思维化考查更趋于明显.笔者认为，思维化成为考查的热点正是基于我们的课程需要培养具备创新型人才的基调，过于代数化的解决方式可以培养大量的熟练操作，却难在思维培养上有所突破，因此可以这么说，图形化解决策略是数形结合思想在向量教学中的最优体现，也是教师教学努力提高学生思维的解决之道.

1.鲍建生.向量教学研究［J］.数学教学，2003（1-3）.

2.郑毓信.向量中学习变式理论的必要发展［J］.中学数学月刊，2006（1）.

3.沈恒.陈旧的问题改进的认识［J］.中学数学（上），2011（11）.

4.姜兴荣.探求解题思路的几种有效策略［J］.中小学数学，2013（7-8）.