核心概念教学要循序渐进和浓墨重彩*
——谈“函数的单调性”的难点突破及概念辨析
2015-06-21安徽省亳州市第一中学
☉安徽省亳州市第一中学 史 嘉
核心概念教学要循序渐进和浓墨重彩*
——谈“函数的单调性”的难点突破及概念辨析
☉安徽省亳州市第一中学 史 嘉
一、引言
数学概念是数学思维的细胞,是形成数学知识体系的基本要素.“如果不先教明概念,便是教得不好的.”(夸美纽斯语)因此,核心概念教学要循序渐进和浓墨重彩.循序渐进,即考虑数学的整体性和思维的系统性,教学设计注重“低起点、高立意”,讲清概念从哪里来、能做什么和到哪里去;浓墨重彩,即课堂教学能突出重点,突破难点,在核心内容上“不惜时、不惜力”,从正反面剖析,多角度深入理解,认清概念的内涵和外延.
2014年12月,笔者参加了第七届全国高中青年数学教师优秀课评比活动.教授课题是“函数的单调性”(共指定八个课题,此是第一个),属于概念课、性质课,也是经典课题.文件附说明:“函数的单调性是最重要的函数性质,在解决实际问题中有着重要作用.要引导学生借助具体函数,经历从图像直观到定性刻画,再到用严格的数学语言刻画的过程.要注意思考如何采取有效措施突破自变量在区间[a,b]上的“任意”取值这一难点.”
二、浓墨重彩奠思维
函数是中学数学的核心概念,而函数的单调性是高中学习函数概念后研究的第一个、也是最重要最基本的性质.函数的单调性及后面的对称性(奇偶性)、周期性,以及高等数学中的有界性和凹凸性,在学习活动的本质上是相同的,都是用抽象的代数式去刻画函数图像的某种几何特征;学习过程也是相似的,都是让学生经历这种探寻抽象的代数式的过程.这个过程历经从直观到抽象、从有限到无限、从直觉到严谨,每一步都是一个很大的思维跨度,而高一学生的思维正处在从经验型向理论型跨越的阶段,他们的逻辑思维水平不高,抽象概括能力不强,代数推理论证能力也比较薄弱,这些都很容易产生思维障碍.因此,函数单调性概念生成的过程正是积累数学活动经验、形成数学思维方式的过程,为后继研究各种具体函数及性质,包括学习导函数的内容奠定了理性思维基础,具有积极的迁移和促进作用.所以,这个过程必须浓墨重彩,让学生亲力亲为.
三、循序渐进破难点
中学数学对函数单调性的认识是“螺旋式上升”的:图像直观(直观化定义)→文字描述(描述性定义)→符号表达(形式化定义)→精确刻画(导函数定义).本节课处在最关键环节,其难点是如何突破用静态的数学符号(不等式)刻画动态的函数变化趋势,其中“任意”一词是最大难点.以增函数为例,我们思考以下几个问题:
(1)为什么要学习函数单调性的形式定义?(回答学习的必要性)
(2)为什么非要从左向右看,从右向左行不行?(遵照x轴正方向)
(3)怎样用数学符号描述自变量x逐渐增大?(抽象出x1 (4)能否检验几个具体数值判断函数单调递增?(几何画板验证) (5)如何做到取遍无穷多个自变量x的值?(逼出任意性) (6)是不是所有的x都要取出来?(强调区间性) (7)取遍所有的x就能保证函数单调递增吗?(比较f(x)的大小,传递性) (8)怎么用数学符号描述因变量y随x的增大而增大?(当x1 围绕上述问题,我们采取递进式“问题串”的形式组织学习材料,分散难点,并寻找已有认知经验,使得函数单调性的形式化定义水到渠成. 下面把这节课的核心环节简述如下. 通过观察一次、二次和反比例函数,明确单调性的相关概念(学习单1的内容),学生心中难免会产生疑问:初中已经学习了函数的单调性,而且利用几何直观很容易判断.为什么高中还要学习函数的单调性(代数证明)呢?为此,我们创设了如下认知冲突情境,让学生意识到学习形式化定义的必要性,在“愤悱”状态下自然开始探索. 学习单2:设置问题,形成冲突. 问题2:(1)图1是函数y=f(x)的图像,它在定义域R上是递增的吗?(先展示该问题,之后推出函数f(x)的解析式为(fx)=0.001x+1) 图1 设计说明:函数图像虽然直观,但是缺乏精确性,必须结合函数解析式;但仅凭解析式常常也难以判断其单调性.以此得出“函数图像不可靠,解析式也不明朗”,为形式化定义的出场“造势”. 学习单3:引导探索,生成新知. 问题3:(1)如何理解“y随着x的增大而增大”,怎样用数学符号表示函数图像的“上升”特征? 以二次函数f(x)=x2在区间[0,+∞)上的单调性为例,用几何画板动画演示“y随x的增大而增大”,生成表格(共15对数据). 设计说明:引导学生借助具体函数,经历从图像直观到定性刻画,再到严格的数学符号刻画的过程.此问题即为从定性描述到定量刻画所搭建的桥梁,充分发挥信息技术,先借助图形、动画和表格等直观感受“y随着x的增大而增大”,引导学生思考“x增大”怎么用符号表示,对应的“y随着增大”又该如何表示?概括出符号表示:若有x1 (2)已知a 拖动“点M”改变函数y=f(x)在区间[a,b]上的图像,可以递增,可以先增后减,也可以先减后增等. 设计说明:此问题是符号化后设法把“任意”一词从学生的潜意识中“逼”出来的开始,要先让学生充分讨论交流,师生对话步步深入,然后借助几何画板动态说明验证两个定点并不能确定函数的单调性. (3)已知a 拖动“点M”,观察函数y=f(x)在区间[a,b]上的图像变化. 设计说明:有了第(2)问作基础,学生很容易判定三个点也不能保证函数在区间[a,b]上递增.取很多点行不行,取无数个点行不行呢?再次让学生展开讨论交流. (4)已知a 设计说明:学生讨论期间,教师要下去巡查,了解学生的观点,先请持赞同观点的学生说明理由,再请持反对意见的学生画图反驳.有意引发争论,强化过程性理解,以此突破难点.然后追问:无数个x还不能保证函数递增,那该怎么办?若学生回答全部取完或任取,追问“总不能一个一个的验证吧?”紧接着师生一起回顾子集的概念,(PPT展示教材上子集定义)回顾对“任意一个”进行操作,突破“无限”的数学方法,再次让学生体验借助代数符号(字母表示数的任意性),用“任意”刻画“无限”的数学思想,感受数学的强大力量和无限魅力. 由学生归纳并完善增函数的形式化定义后,很快类比出减函数的定义,然后紧跟下面一组判断题: 你认为下列说法是否正确,请说明理由. ①设函数y=f(x)的定义域为[a,+∞),若对任意x>a,都有f(x)>f(a),则y=f(x)在区间[a,+∞)上递增; ②设函数y=f(x)的定义域为R,若对任意x1,x2∈(a,+∞),且x1>x2,都有f(x1)>f(x2),则y=f(x)是递增的; ④设函数y=f(x)的定义域为R,任取x1,x2∈R,且x1≠x2,都有<0,则y=f(x)是递减的. 设计说明:通过辨析正、反例帮助学生对概念再次进行深入思考,逐步形成对概念本质正确、全面而深刻的理解,这是对概念的及时巩固,也是丰富其内涵和外延,更是培养学生批判性思维和严谨性思维的绝好机会.总之,要体现并强调“回到定义”思考问题的重要性. 在备课时,笔者对比研读了六套教材,发现各版本有关函数单调性概念的表述略有差异,归类罗列如下,供读者朋友思考. 以增函数为例,六套教材的定义句式基本相同: 一般地,设函数y=f(x)的定义域为D,区间I⊆D.如果对于区间I内的任意两个值x1,x2,当x1 (1)(人教A版和B版)就说函数f(x)在区间I上是增函数.如果函数y=f(x)在区间I上是增函数或减函数,那么就说函数y=f(x)在这一区间具有(严格的)单调性,区间I叫y=f(x)的单调区间. (2)(苏教版和上教版)就说y=f(x)在区间I上是单调增函数,I为y=f(x)的单调增区间. (3)(湘教版)就说f(x)是区间I上的递增函数.如果函数y=f(x)是区间I上的递增函数或递减函数,就说f(x)在区间I上严格单调,区间I叫做f(x)的严格单调区间. (4)(北师大版)就称函数y=f(x)在区间I上是增加的,有时也称函数y=f(x)在区间I上是递增的. 一般地,对于函数y=f(x)的定义域内的一个子集I,如果对于任意两数x1,x2∈I,当x1 对比定义发现有两大差异: 第一,增函数名称的差异. 人教A版和B版称为增函数,苏教版和上教版称为单调增函数,湘教版称为递增函数,即这五个版本都直接称函数y=f(x)是区间I上的(单调或递)增函数.只有北师大版称函数y=f(x)在区间I上是增加的,并且明确指出,当函数y=f(x)在整个定义域内是增加的,才称这个函数为增函数. 定义域是函数的生命之域,函数的一切性质都是依存在定义域上的.而函数的单调性对区间具有更加直接的依存性,没有区间就谈不上单调性.函数在区间I上具有“任意两数x1,x2∈I,当x1 第二,区间和数集的差异. 六个版本定义时都指出了I是定义域D的子区间,但只有北师大版又另外指出了函数在数集I上具有单调性.我们知道,区间一定是数集,但数集不一定是区间.看来前五个版本教材只是定义在区间上的单调性,并没有拓展到一般的数集上.事实上,单调性并非只有在区间上才能研究,在一般的数集上也是可以研究的,比如数列. 高等数学中函数单调性概念是怎么定义的呢,我们看看颇具影响力的华东师大版《数学分析》中的定义:设f为定义在数集D上的函数,若对任何x1,x2∈D,当x1 初等数学是高等数学的基础,高等数学是初等数学的延伸和发展.相同的概念,比如函数的单调性,还是尽可能统一的好. 李邦河院士曾告诫我们“数学根本上是玩概念的”.那么,如何在教学实践中“玩概念(尤其是核心概念)”?可谓见仁见智.章建跃先生认为,数学中“玩概念”包含两个方面:一是定义概念,二是利用概念研究数学规律. 因此,对于数学核心概念教学,我们要继承我国“双基”教学的传统,挖掘其内涵和外延,即重视基础知识、基本技能训练和能力的培养;更要践行新课程理念,引导学生通过自主探究建构数学概念、性质等的雏形,即注重基本数学活动经验、基本数学思想方法的体验和提炼.在“玩”的过程中,归纳、抽象出变化中的不变性、规律性和特殊性等基本内容. 1.中华人民共和国教育部.普通高中数学课程标准[M].北京:人民教育出版社,2003. 2.张婕.新课程理念下的数学概念教学实施与思考[J].中学数学(上),2015(5). 3.刘宗博,罗新兵.用活教材,让学生经历概念的形成过程[J].中学数学教学参考(上),2014(11). 4.刘绍学.数学(A版必修1)[M].北京:人民教育出版社,2012. 5.高存明.数学(B版必修1)[M].北京:人民教育出版社,2007. 6.严士健,王尚志.数学(必修1)[M].北京:北京师范大学出版社,2014. 7.单墫.数学(必修1)[M].南京:江苏教育出版社,2012. 8.张景中,黄楚芳.数学(必修1)[M].长沙:湖南教育出版社,2013. 9.袁震东.数学(高一年级第一学期)[M].上海:上海教育出版社,2009. 10.华东师范大学数学系.数学分析[M].北京:高等教育出版社,2010. *本文系安徽省教育规划课题《“文化数学”理念下高中数学学习单的实践研究》(项目编号:JG13105)和《基于基本活动经验的高中数学教学实践研究》(项目编号:JG14071)的部分研究成果.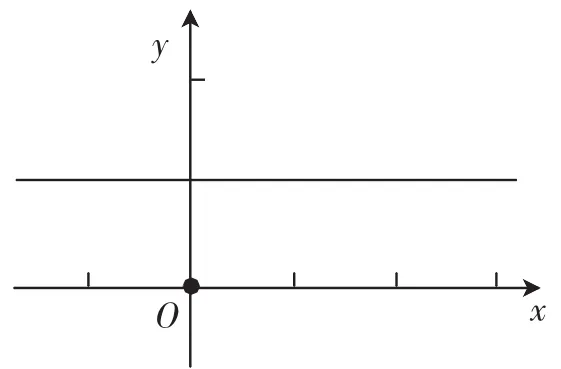
四、求同存异待商榷
五、结束语
