剪不断理还乱的条件概率——引例梳理条件概率思维

☉江苏省口岸中学 高国圣

剪不断理还乱的条件概率
——引例梳理条件概率思维

☉江苏省口岸中学 高国圣

引例：一个家庭中有两个小孩，假定生男生女是等可能的，已知这个家庭有一个是女孩，问：这时另一个孩子是男孩的概率是多少？

条件概率指的是在事件A发生的条件下，事件B发生的概率.教师在讲解此题时，学生普遍认为答案是究其原因是没有理解条件概率的内涵，因此可让学生回答如下三个问题.

问题1：一个家庭中有两个小孩，可能有几种情况？

答：（男，男）（男，女）（女，男）（女，女）.

问题2：其中一个是女孩，有几种情况？

答：（男，女）（女，男）（女，女）.

问题3：在其中一个是女孩的条件下，另一个是男孩的概率？

至此问题不攻自破.

对于条件概率的理解，笔者结合自己的教学经验，建议从如下几方面入手，供参考.

一、借助图示法理解条件概率的本质

图1

如图1，设A、B是两个事件，且P（A）＞0，在事件A已发生的条件下，事件B发生的概率称为条件概率，记作P（B|A）．从图示法的角度来看，这个定义可以理解为：

事件的样本点已落在图形A中（事件A已发生），问落在B中（事件B发生）的概率．由于样本点已经落在A中，且又要求落在B中，故只能落在AB中．在这种观点下，原来的的样本空间Ω（即基本事件的范围）变为已知的条件事件A所对应的空间，原来的事件B对应的空间变为事件AB对应的空间．因此，条件概率问题可以看成“样本空间减少”的条件下的古典概型或几何概型问题．

例1（2011年高考辽宁卷）从1、2、3、4、5中任取2个不同的数，事件A＝“取到的2个数之和为偶数”，事件B＝“取到的2个数均为偶数”，则P（B|A）＝（）.

评析：在“减少样本空间”的观点下，条件概率P（B|A）的计算公式为其中，在古典概型中，n（A）与n（AB）分别表示事件A与事件AB所包含的基本事件的个数.

二、弄清P（B|A）与P（AB）的区别

P（AB）与P（B|A）是两个截然不同的事件的概率，P（AB）表示事件A与B同时发生的概率，而条件概率P（B|A）表示在事件A已经发生的条件下事件B发生的概率.

例2（2015年高考陕西卷）随机抽取一个年份，对西安市该年4月份的天气情况进行统计，结果如下：

?

（Ⅰ）在4月份任取一天，估计西安市在该天不下雨的概率；

（ⅠⅠ）西安市某学校拟从4月份的一个晴天开始举行连续两天的运动会，估计运动会期间不下雨的概率.

解析：（Ⅰ）在容量为30的样本中，从表格中得不下雨的天数是26，以频率估计概率，从4月份任选一天，西安市不下雨的概率是

（ⅠⅠ）称相邻两个日期为“互邻日期对”（如1日与2日，2日与3日等），这样在4月份中，前一天为晴天的互邻日期对有16对，其中后一天不下雨的有14个，所以晴天的次日不下雨的频率为，以频率估计概率，运动会期间不下雨的概率为

评析：在解题中需注意P（B|A）与P（B）的关系：计算P（B）是在整个样本空间Ω上考虑事件B发生的概率，计算P（B|A）是在A发生的范围内来考虑事件B发生的概率.样本空间从Ω减少为A，往往会导致无条件概率P（B）与条件概率P（B|A）并不相等.若事件A与B是相互独立事件，则P（B）=P（B|A）.

三、几何概型下的条件概率问题

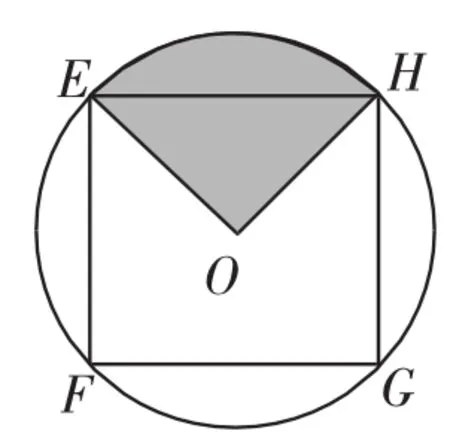
图2

例3（2011年高考湖南卷）如图2，EFGH是以O为圆心、半径为1的圆的内接正方形．将一颗豆子随机地扔到该圆内，用A表示事件“豆子落在正方形EFGH内”，B表示事件“豆子落在扇形OHE（阴影部分）内”，则（1）P（A）＝______；（2）P（B|A）＝______.

四、概率性质的应用

例4（2013年高考新课标Ⅰ卷）一批产品需要进行质量检验，检验方案是：先从这批产品中任取4件作检验，这4件产品中优质品的件数记为n.如果n＝3，再从这批产品中任取4件作检验，若都为优质品，则这批产品通过检验；如果n＝4，再从这批产品中任取1件作检验，若为优质品，则这批产品通过检验；其他情况下，这批产品都不能通过检验．假设这批产品的优质品率为50%，即取出的每件产品是优质品的概率都为且各件产品是否为优质品相互独立．

（1）求这批产品通过检验的概率；

（2）已知每件产品的检验费用为100元，且抽取的每件产品都需要检验，对这批产品作质量检验所需的费用记为X（单位：元），求X的分布列及数学期望．

解析：（1）设第一次取出的4件产品中恰有3件优质品为事件A1，第一次取出的4件产品全是优质品为事件A2，第二次取出的4件产品都是优质品为事件B1，第二次取出的1件产品是优质品为事件B2，这批产品通过检验为事件A，依题意有A＝（A1B1）∪（A2B2），且A1B1与A2B2互斥，所以P（A）＝P（A1B1）＋P（A2B2）＝P（A1）P（B1|A1）＋

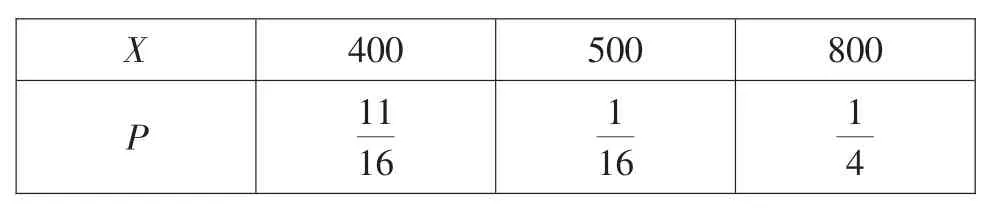
（2）X可能的取值为400、500、800，并且P（X＝400）＝所以X的分布列为

?

评析：若事件A发生了，事件B才有可能发生；若事件A没有发生，事件B就不可能发生了.反过来，若事件B发生了，事件A必然发生了，即事件A、B都发生了.事件A发生是事件B发生的必要不充分条件.也就是说，“事件A发生的条件下，事件B发生”中的条件是“事件B发生”的条件.此时，P（B）=P（AB）=P（A）P（B|A）.本题是概率的综合问题，掌握基本概念及条件概率的基本运算是解决问题的关键.

总之，条件概率有着较广泛的应用，而且对于进一步加深对概率问题的理解和学习概率也有着实际意义.如何把握好难度，使学生正确地理解条件概率的概念和它的计算方法，对于加深学生对概率问题的理解和进一步学习概率都有着重要的意义.