从2015年广东高考文数21题的解决挖掘其教育价值
2015-06-21广东省东莞市东莞中学庞进发
☉广东省东莞市东莞中学 庞进发
从2015年广东高考文数21题的解决挖掘其教育价值
☉广东省东莞市东莞中学 庞进发
一年一度的高考已结束,全国的高考试题成为教师们关注和研究的热点.高考试题主要由高校的学科专家命制而成,深刻地体现了其选拔性,以及高校对中学教学的期望和学生知识能力的要求,并且给中学的教学及高三备考指明了方向.例如,2015年广东高考数学试题,注重数学基础知识、数学本质及数学核心素养的考查,意在中学数学教学要重视知识的形成过程、数学本质的理解,重视数学教材的示范作用,回到教材.而教师们对高考试题的研究,更多的是停留在数学知识的应用及数学问题的解决上,思考其教育价值的不多.本文笔者从2015年广东高考文数21题(下文简称“试题”)的解决挖掘其教育价值.
试题:设a为实数,函数f(x)=(x-a)2+|x-a|-a(a-1).
(1)若f(0)≤1,求a的取值范围;
(2)讨论f(x)的单调性;
本题主要考查函数的单调性、零点等性质,以带绝对值的二次函数为背景,考查了推理论证和运算求解能力,以及分类讨论、数形结合等数学思想方法.本题看似容易,实际想拿到高分或满分,必须对数学概念非常清晰,深刻领悟数学思想方法,需要考生具备很强的逻辑思维能力,以及良好的解题习惯.从广东省文科考生的答卷情况看,本题很好地体现了其选拔性,同时在解决的过程中,也蕴含着深刻的教育价值.
一、强调对数学概念、本质的透彻理解
通常解决一个数学问题,首先需要结合问题情景联想所学的数学知识,然后在数学知识与问题情景的理解中认知数学问题,进而进行合理的数学推理、运算,寻找问题的条件与结论之间的内在联系或矛盾.因此深刻理解数学概念、本质,对于数学问题的解决尤为重要.“试题”考查了绝对值的概念及函数零点存在性定理的概念.从答卷的情况发现,文科考生是在初中学习了绝对值,并且要求不高,对绝对值的概念理解不透彻,在高中又没有进一步学习,所以很多考生不能正确地去掉绝对值符号,以致解决“试题”第(1)问时没有对a的正负进行讨论,直接去掉绝对值进行运算.典型错误如:f(0)=(0-a)2+|0-a|-a(a-1)=a2+a-a2+a≤1,2a≤1,得.还有函数零点存在性定理,绝大部分文科考生在高一学习时都是在形的方面进行直观的了解,缺乏对存在零点时函数值关系的深刻理解,导致在判断零点的个数时,由一个最值点就得出零点个数的结论,而忽略了对单调区间另一个端点函数值正负的判断.如解决“试题”第(3)问时,设证明得到F(x)在(0,a]上单调递减,在[a,+∞)上单调递增,得到F(x)的最小值为F(a),因为a> 2,所以F(a)=a2-2a2+a+所以在(0,+∞)内有两个零点.错误原因在于没有分别判断在单调区间(0,a]和[a,+∞)中另一个端点函数值的正负号.正确的表述应该补充上F(1)=1-2a-1+这也启发我们,在高一、高二的数学教学中,要注重数学概念知识的形成过程,深刻理解数学概念的本质,为数学问题的解决打下坚实的基础.而避免高一、高二教学“高三”化,数学概念教学蜻蜓点水,做大量的题型练习.
二、体现多种数学思想方法
华南师范大学数学科学学院刘秀湘教授在2014年广东高考数学评卷总结中提到:“在教学中,教师应该以问题为驱动,培养学生提出问题、分析问题和解决问题的能力;教师自身要有研究问题的意识,在教学中提出问题、分析问题和解决问题,特别是讲清楚问题或者解题方法的来龙去脉及其规律,交给学生一把钥匙——数学的思想,只有它才能真正带领学生叩开数学的大门.”可见数学思想、方法作为数学学科的“一般原理”,在数学学习中是至关重要的.因此,在教学中要善于挖掘数学问题解决过程中所蕴含的数学思想方法,特别是一些经典的高考试题的解决.如“试题”第(3)问,不同的解决过程,就蕴含着多种数学思想方法.
1.由特殊到一般的数学思想方法
由特殊到一般的数学思想方法就是对于某个一般性的数学问题,如果一时难以解决,那么可以先解决它的特殊情况,即从研究对象的全体转变为研究属于这个全体中的一个对象或部分对象,然后再把解决特殊情况的方法、结论应用或者推广到一般问题上,从而获得一般性问题的解答.“试题”第(3)问是对于a≥2的情况下讨论f(x)在区间(0,+∞)内的零点个数,可以先对于a= 2特殊的情形进行讨论,由于函数去掉绝对值后是一个分段函数,因此分别在(0,2]和(2,+∞)两个区间上讨论其零点的个数.接着再对更一般的情形a>2进行讨论,类比上述的研究方法,分别在(0,a]和(a,+∞)两个区间上讨论其零点的个数,从而得到问题的解答.
又因为F(2)=0,故有唯一零点x=2.
(Ⅱ)当a>2时,
①当0 ②当x>a时,因为F′(x)=2x-(2a-1)-所以F(x)在[a,+∞)上为增函数. 2.数形结合的数学思想方法 数形结合即数形渗透,两者相互推进,层层深入,这样就能使复杂问题简单化,抽象问题直观化,是中学数学中常见的解题思想和方法,经常应用在研究函数、解析几何等问题中.“试题”第(3)问,也可以把内的零点个数问题等价于函数在 a|-a(a-1)与图像在(0,+∞)内的交点个数问题,结合几何图形直观快捷地得出答案. 图1 因为f(x)在[a,+∞)上是增函数,在(-∞,a]上是减函数,所以当x=a时,f(x)取得最小值fmin(x)=f(a)=-a2+ a. 3.化归与转化的数学思想方法 化归与转化的思想就是将未知解法或难以解决的问题,通过观察、分析、联想、类比等思维过程,选择恰当的方法进行变换,化归为在已知知识范围内已经解决或容易解决的问题的数学思想.化归与转化的思想是解决数学问题的根本思想,解题的过程实际就是转化的过程.“试题”第(3)问,把在(0,+∞)内零点个数问题转化为xf(x)+4在(0,+∞)内零点个数问题,当x≥a时,g(x)=x3+(1-2a)x2+4有零点又等价于在[a,+∞)上有交点,通过分离参数,化归为研究在[a,+∞)上的值域问题,更容易解答. 当x≥a时,g(x)=x3+(1-2a)x2+4有零点等价于在[a,+∞)上的交点个数. 因为x≥a≥2,所以h′(x)≥0恒成立,所以h(x)在[a,+∞)上单调递增. 又a≥2,所以a-2≥0. 当0 Δ=4(1+2a)2-4×3×2a=4(4a2-2a+1)>0. 由g′(x)<0,解得x0 由g′(x)>0,解得0 所以g(x)在(0,x0]上递增,在[x0,a)上递减. 当a=2时,因为g(0)=4>0且g(2)=23+(1-2×2)×22+4= 0,所以g(x)=xf(x)+4在(0,2)内没有零点. 当a>2时,因为g(0)=4>0且g(a)=a3+(1-2a)a2+4= -(a-2)(a2+a+2)<0,所以由根的存在性定理,g(x)=xf(x)+4在(0,a)内有且只有1个零点. 4.整体的数学思想方法 整体思想,就是在研究和解决有关数学问题时,通过研究问题的整体形式、整体结构、整体特征,从而对问题进行整体处理的解题方法.从整体上去认识问题、思考问题,常常能化繁为简、变难为易,同时又能培养学生思维的灵活性、敏捷性.“试题”第(3)问,首先从整体上研究F(x)的单调性,得出F(x)在(0,a)上单调递减,在[a,+∞)上单调递增,求出F(x)的最小值F(a),然后判断F(a)的正负,结合函数图像,依据零点存在性定理,得出结论. 解法4:f(x)=x2-2ax+|x-a|+a,设F(x) 当x≥a时,F(x)=x2-2ax+x则F′(x)=2x-2a+1- 当0 所以F(x)在(0,a)上单调递减,在[a,+∞)上单调递增. 所以Fmin(x)=F(a)=a2-2a2+a+0(a≥2). “试题”从文科考生答卷反馈的情况估计得5分以上的考生只有0.34%,有51%考生得0分,体现了“试题”有很好的选拔性,同时也暴露了学生数学问题解决的缺失. 1.寻找问题切入点意识薄弱 “试题”从得0分的考生比例可见,学生寻找问题切入点意识比较薄弱.解决数学问题重要的是能准确找到解题的切入点,而寻找切入点的关键是紧扣数学的有关概念.如“试题”中,就是紧扣绝对值的概念,进行分类讨论解决;紧扣函数的概念,首先研究函数的定义域,再研究函数的模型结构及其性质.典型的错误如:“试题”的第(2)问分类去掉绝对值判断单调性时没有紧扣函数的定义域,当x>a时,f′(x)=2x-2a+1>0,所以f(x)在上单调递增,在上单调递减;当x 在教学中,我们要善于挖掘数学问题的教育价值,做到精讲精练.这样既能减轻学生的负担,又能很好地促进学生的发展,进一步提高课堂效率.上述只是从数学问题解决中涉及的数学概念、本质的理解,蕴含的数学思想方法,暴露学生数学问题解决的缺失等方面挖掘“试题”的教育价值.而数学问题的教育价值还有很多方面,不同的数学问题又蕴含着不同的教育价值,有待进一步探讨. 2.存在解题定势思维 数学解题思维定势是指解题者在解决数学问题的思维过程中表现出来的思维的定向预备状态.在解决某些数学问题的过程中,需要克服定势思维.“试题”第(1)问估计有6%的文科考生进行去绝对值求导,如:因为f(x)=x2-2ax+a+x-a,所以f′(x)=2x-2a+1,当f′(x)=0时,…….文科考生形成了拿到函数问题就求导的定势思维.这也启发我们在教学中要教会学生分析问题的一般方法,培养学生数学思维的灵活性,避免思维的固化. 3.运算推理能力欠缺 据调查研究发现,目前部分高中学生运算推理能力的状况很差,严重影响其高中数学学习,这部分学生在高中数学学习中一讲就懂,一做就错,结果出现“会而不对,对而不全”的情形.文科考生在“试题”的解答过程中,运算推理能力欠缺暴露无遗.典型的错误,如:第(1)问代入后不知道如何化简或化简出错,若f(0)≤1,则f(0)=(0-a)2+|0-a|-a(a-1)≤1,得f(0)=a2+|a|≤1,当a≥0时,2a+a≤1,得 1.中华人民共和国教育部.普通高中数学课程标准(实验)[M].北京:人民教育出版社,2003. 2.何小亚.与新课程同行:数学学与教的心理学[M].广州:华南理工大学出版社,2003. 3.王林全.当代中小学数学课程发展[M].广州:广东教育出版社,2006. 4.章建跃,陶维林.概念教学必须体现概念的形成过程[J].数学通报,2010(1). 5.刘秀湘.在稳定中注重数学概念和思维的考查[J].中学数学研究,2014(8). 6.【美】G.波利亚,著.怎样解题[M].涂泓,冯承天,译.上海:上海科技教育出版社,2007.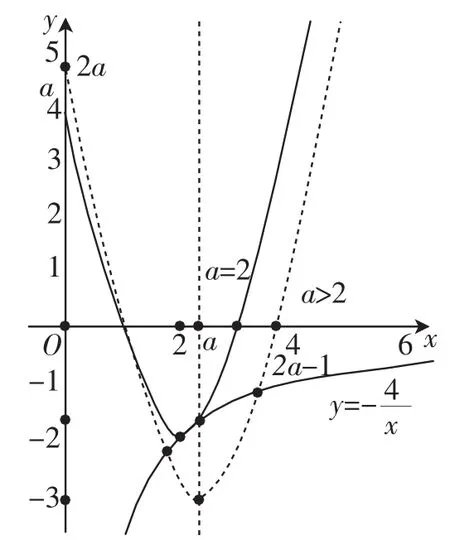
三、暴露学生数学问题解决的缺失
