基于改进BP神经网络的逆变电路故障诊断

廖俊勃，帕ξ来·马合木提，蔡鑫，周浩

(新疆大学电气工程学院，新疆乌鲁木齐830047)

基于改进BP神经网络的逆变电路故障诊断

廖俊勃，帕ξ来·马合木提，蔡鑫，周浩

(新疆大学电气工程学院，新疆乌鲁木齐830047)

针对BP神经网络鲁棒性、容错性不强的问题，提出双向BP神经网络，更直接地建立与先前状态的映射关系；利用量子粒子群算法(QPSO)优化双向BP神经网络的权值和阈值，克服其学习算法复杂、收敛速度慢的缺点，来得到精度更高的网络。将改进的双向BP神经网络应用于逆变电路的故障诊断，测试结果表明该算法比双向BP神经网络具有更强的收敛性和精确率，为逆变电路的故障诊断提出一个新的思路。

双向BP神经网络；量子粒子群算法；逆变电路；故障诊断

随着电力电子技术的迅猛发展，电力电子技术设备广泛应用于国防军事和工业生产。同时电力电子电路的故障问题也越来越突出，电力电子设备一旦发生故障，可能造成装置或系统的损坏甚至威胁到生命财产安全。设计合理的诊断方案来解决电力电子电路中出现的问题是现代研究的重点。吴小华[1]提出一种基于BP神经网络的电力电子逆变系统故障诊断，并且以DSP为核心的在线故障检测与诊断系统，对逆变器主电路开关管进行开路故障诊断，但是其缺点是神经网络的泛化能力不够，故障诊断率不高。张洪涛[2]提出一种基于小波分析和神经网络的逆变器开路故障诊断方法，有较高的精度和实时性，但不能进行故障元件的精确定位。标准BP神经网络引入逆变电路故障诊断中取得了较好的效果，但当故障模式较多时，网络结构较为复杂，尤其是遇到复合故障时，分辨效果较差。

本文构造双向BP神经网络结构，提出一种量子粒子群算法(QPSO)。QPSO算法解决了粒子群(PSO)算法搜索空间有限、搜索精度不高、易陷入极小值等缺点，用来优化双向BP神经网络权值和阈值，并将其应用于逆变电路的故障诊断，结合了QPSO和BP算法的优点，具有训练快速和全局收敛的优点。

1 双向BP神经网络

双向BP神经网络相比于传统的BP神经网络更直接地建立与先前状态之间的映射关系，使相邻层的两个神经元之间存在两个相反方向的连接，其拓扑结构如图1所示。

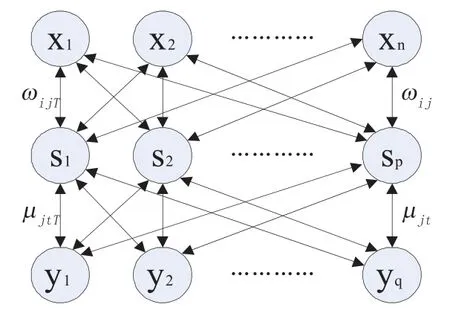
图1 双向BP神经网络结构示意图

双向BP神经网络是由前向传播过程和反向传播过程构成[3]，前向传播就是经典的BP神经网络训练过程。

(1)输入层各节点的输出为：

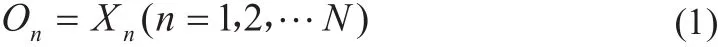
(2)隐层和输出层输入分别为：

反向传播过程主要讨论其权值调整，即：

(1)隐层到输出层前向权值：

(2)隐层到输出层后向权值：

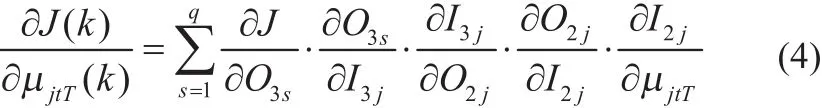
(3)输入层到隐层前向权值：

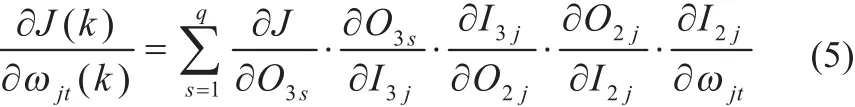
(4)输入层到隐层后向权值：

双向BP神经网络在节点数不变的情况下，引入先前时刻状态，建立了反向连接，使其具有更强的鲁棒性、容错性和逼近能力，但BP神经网络收敛速度慢、局部极值等缺点仍未消除。

2 改进的双向BP神经网络

2.1 量子粒子群算法

PSO是一种进化计算技术[4]，在对动物集群活动行为观察的基础上，利用群体中的个体对信息的共享使整个群体的运动在问题求解空间中产生从无序到有序的演化过程，从而获得最优解，基于PSO的BP神经网络学习算法已经得到了广泛的应用[5-7]。由于粒子具有量子的行为，可以在整个可行解空间中进行搜索，解决了PSO算法搜索空间有限、搜索精度不高、易陷入极小值等缺点。根据这种思想提出QPSO[8]，对整个PSO算法进行搜索策略的改变，并且进化方程中不需要速度向量，使其形式更简单，参数更少，更易于控制。

在QPSO中，假设了每个粒子的量子态，制定了波函数来描述粒子的状态，并通过Monte Carlo方法来解得粒子在空间某一点出现的概率密度[9]。

引入一个全局点mbest来计算粒子的迭代变量L，定义了所有粒子的局部最好位置的平均值。

2.2 用QPSO改进双向BP神经网络

双向BP神经网络虽然改进了标准BP神经网络，但是随着规模变大，函数变复杂，BP神经网络的缺陷仍然存在，通过QPSO优化BP神经网络的权值和阈值，相比PSO优化BP神经网络，能得到全局最优解。

本文采用的双向BP神经网络的隐藏层和输出层的作用函数为Sigmoid函数，用QPSO优化双向BP神经网络时，粒子群的位置向量是所训练的双向BP神经网络的权值和阀值。输入训练样本进行训练，对每一个网络训练集上产生的均方差进行计算：

QPSO算法改进双向BP神经网络的步骤：

步骤1：根据给定的输入特征参数样本数据设定其神经网络拓扑结构。

步骤2：选定粒子数，初始化粒子的mbest和pbest，并开始对输入样本进行训练。

步骤3：根据双向BP神经网络的算法和公式(13)计算粒子的适应度函数，以此来评价每一个粒子，经过不断的对比和更新得到mbest和pbest。

步骤4：判断是否满足算法的终止条件(达到最小误差要求)，若满足则转到步骤6，若不满足则转到步骤5。

步骤5：按量子粒子群计算模型生成新的个体，转到步骤3。

步骤6：输出当前具有最优适应度的粒子参数结果。

3 改进的双向BP神经网络在逆变电路中的应用

以三相桥式电压源逆变电路为例，其电路结构如图2所示。

逆变电源上的开关原件通常有独立的基极驱动电路驱动，驱动电路单元的故障通常表现为驱动电源失效，元件击穿或开路，逆变电源在实际运用中出现比较多的故障往往是功率半导体元件(IGBT)的断路与短路故障[11-12]。由于篇幅原因，在本论文中仅对单个IGBT开路故障做一分析。

对三相桥式逆变电路的故障分类进行编码，使用六位编码(X1X2X3X4XX5X6)表示，其中=1或0。故障代码的高三位代表故障类型，低三位代表故障晶闸管的位置(正常表示为：001000)，如表1所示。

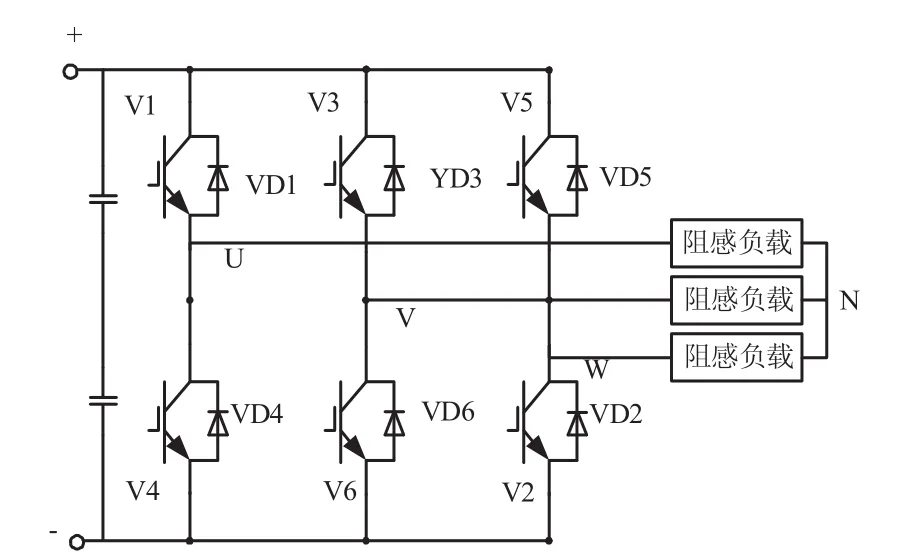
图2 三相桥式电压源逆变电路结构图

表1 故障分类表示

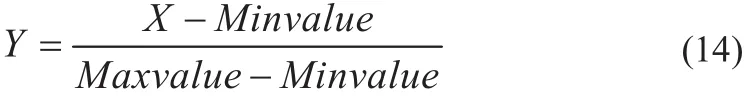
式中：、分别为转换前和转换后的值；、分别为样本的最大值和最小值。

搜索400组确定的逆变电路故障数据，选取300组作为网络训练样本，100组用于识别逆变电路故障。其训练样本如表2所示。

表2 网络训练样本组成

选用三层双向BP神经网络，由诊断实例可知，需要4个输入层神经元和6个输出层神经元。神经网络隐含层神经元数的确定没有明确的理论依据可寻，只能通过选取不同的隐含层神经元对网络进行训练，根据训练结果确定最佳的隐含层神经元数。隐层节点数太多或太少，都会使得迭代次数增加，而且隐层节点数太多，会使网络复杂化。考虑各种因素，经过一系列的仿真实验进行对比，选择隐层节点数为9的神经网络。本文QPSO算法中参数β从0.9到0.3线性减小，网络误差精度取0.001，学习速率为0.01。分别用双向BP神经网络和QPSO改进的双向BP神经网络进行训练，训练结果如图3、图4所示。

对比图3、图4的仿真结果可轻易发现，在逆变电路的故障诊断中QPSO改进双向BP神经网络的算法收敛速度比双向BP神经神经网络的算法曲线快，当达到相同的精度时改进双向BP神经网络的算法次数为49次，而QPSO改进的双向BP神经网络只需17次。

图3 QPSO优化的双向BP神经网络的算法曲线

图4 双向BP神经网络的算法曲线

采用已经训练好的神经网络，对样本库中的100个检验样本进行故障诊断，识别结果如表3所示。

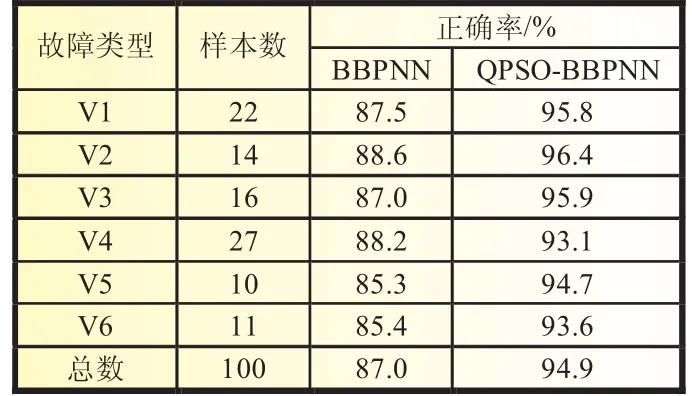
表3 各部分故障比较

由表3可以看出QPSO-BBPNN算法具有优越性，总的正确率达到了94.9%，与双向BP神经网络(正确率为87.0%)相比，表现出强烈的泛化能力，证明了基于QPSO改进的双向BP神经网络对逆变电路的故障诊断是有效的，而且比双向BP神经网络的准确率更高。

4 结论

本文采用QPSO算法对双向BP神经网络进行优化，不仅使改进的双向BP神经网络在学习速率上比常规的双向BP神经网络有了很大的提高，而且使其收敛性更好。改进的双向BP神经网络提高了逆变电路故障诊断的准确性和可靠性，为逆变电路的故障诊断提供了一种可靠的方法。

[1]吴小华,史忠科,张晓斌.基于DSP三相逆变电路在线故障诊断研究设计[J].电力电子技术,2004,38(2):37-39.

[2]张洪涛，安庆.基于小波变换和神经网络的逆变电路故障诊断方法[J].计算机测量与控制,2010,18(6):1273-1276.

[3]邵克勇,李飞,蒋北艳,等.基于改进遗传算法的双向BP神经网络控制[J].化工自动化及仪表,2010,37(10):18-21.

[4]EBERHART R C,SHI Y H.Particle swarm optimization:developments,applications and resources[C]//Proceedings of the 2001 Congress on Evolutionary Computation.Piscataway:IEEE Press, 2001.

[5]李祚泳,汪嘉杨,郭淳.PSO算法优化BP网络的新方法及仿真实验[J].电子学报,2008,36(11):2224-2228.

[6]潘昊,侯清兰.基于粒子群算法的BP网络学习研究[J].计算机工程与应用,2006,42(16):41-43.

[7]江丽,王爱平.基于粒子群与BP混合算法的神经网络学习方法[J].计算机应用,2012,32:13-15.

[8]SUN J,XU W B.A global search strategy of quantum-behaved particle swarm optimization[C]//Proceedings of IEEE Conference on Cyberence on Cybernetics and Intelligent Systems.USA:IEEE Press, 2004:111-116.

[9]FANG W,SUN J,DING Y R,et al.A review of quantum-behaved particle swarm optimization[J].IEEE Technical Review,2010,27(4): 336-348.

[10]SUN J,FENG B,XU W.Particle swarm optimization with particles having quantum behavior[J].IEEE,2004(1):325-331.

[11]汤清泉,颜世超,卢松升,等.三电平逆变器的功率管开路故障诊断[J].中国电机工程学报,2008,28(21):26-32.

[12]张兰红,胡育文,黄文新.三相变频驱动系统中逆变器的故障诊断与容错技术[J].电工技术,2004,19(12):1-9.

Fault diagnosis of inverter circuit based on improved bidirectional BP neural network

LIAO Jun-bo,PAZILAT Mahemuti,CAI Xin,ZHOU Hao

A kind of bidirectional BP neural network(BBPNN)was proposed aiming at BP neural network which robustness and fault tolerance was not strong.Reverse connection was established between adjacent layer neurons directly to draw the previous state variables of the system into the network.In order to overcome learning algorithm complexity and slow convergence,quantum particle swarm optimization(QPSO)was used to optimize weights and thresholds of BP neural network.In this way,the network could be obtained with higher accuracy.Improved bidirectional BP neural network was applied to the inverter circuit fault diagnosis.Test results show that the algorithm has stronger convergence and accuracy than BBNPP.A new way for the inverter circuit fault diagnosi was proposed.

bidirectional BP neural network;quantum particle swarm optimization;inverter circuit;fault diagnosis

TM 464

A

1002-087 X(2015)03-0574-04

2014-08-07

国家自然科学基金(61364010)

廖俊勃(1987—)，男，陕西省人，硕士，主要研究方向为过程检测、诊断与控制技术(含风力发电)。