高职数学实验课程教学研究

陈允峰

【摘要】传统高等数学教育教学模式偏重于理论讲授，为了讲授知识而讲授知识，忽视了学生的数学应用能力的培养，我们可以通过引入数学实验将这种情况加以改善，数学实验与高等数学教学相结合的具体模式有：运用计算机多媒体辅助数学实验教学;结合专业知识和实际问题来安排学生的动手实验课。

【关键词】数学实验  案例教学  matlab  lingo软件

【中图分类号】G71 【文献标识码】A 【文章编号】2095-3089（2015）05-0139-01

1.数学实验简介

目前数学实验还没有一个规范统一的定义，就目前而言，我们一般认为数学实验是以数学理论知识作为原理，结合计算机技术进行软件编程、图形可视化和数值计算等为实验内容，以实际生产、生活问题和数学教材经典案例为实验对象，以计算机作为工具，以分析建模、模拟仿真软件求解和总结推广为主要实验方法，并以实验报告为最终体现形式的实践活动。数学实验的主要任务就是引导学生将实际问题转化为数学模型，再运用现代的计算机技术和数学专业软件（如SPSS，Matlab，Lingo，mathematic等）来进行数学推演和数值计算，以求出实验结果，进而解决实际问题。

2.高等数学科课程内容的选择

高等数学实验课的内容选择应当遵循新的课程建设标准：数学实验课应当将专业需求、和实际生活中的问题放在首位，从其中总结出经典案例作为实验课的基本内容在我们的教学实践中，总结了一些经济管理类相关专业的经典案例大家可以作为参考：

案例1：

美国1790年、1800年、…、2000年（时间间隔10年）的人口分别为：3.9、5.3、7.2、9.6、12.9、17.1、23.2、31.4、38.6、50.2、62.9、72.0、92.0、106.5、123、132、151、179、204、227、251、281（单位：百万）。

请根据美国1790年到2000年的美国人口数据预测美国在未来的2010、2020、…，2050年的人口数。

分析：

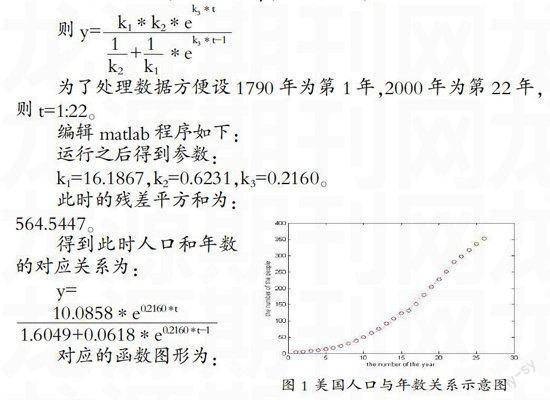
首先做出1790年到2000年的人口数散点图（图1中红色圆圈所示），可以看出，美国人口从1790年开始有一阶段人口增长缓慢，然后又经历了大概100年的快速发展阶段，然后增长速度逐渐放缓。因此美国人口增长模型适合logistics阻滞增长模型。

设时间为t年，人口数为y（单位：百万）。

则y=■

为了处理数据方便设1790年为第1年，2000年为第22年，则t=1：22。

编辑matlab程序如下：

运行之后得到参数：

k1=16.1867，k2=0.6231，k3=0.2160。

此时的残差平方和为：564.5447。

得到此时人口和年数的对应关系为：

y=■

对应的函数图形为：

美国在未来的2010、2020、…，2050年的人口数依次为：297.6186  317.9635  336.4972  353.0794  367.6781（单位：百万）。

案例2：

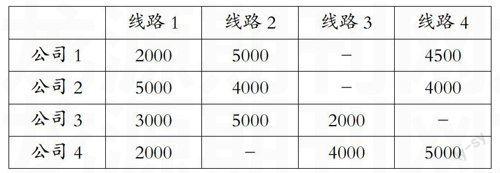
某城市体育委员会组织一次大型的羽毛球比赛，需要为此次赛事新增四条公交线路，四家公交公司做出以下竞标（每条线路价格单位：元）：

假设每位竟标者至多可分配到两条线路，问委员会将如何招标？

解题分析：此题为0-1规划模型，运用lingo软件编程即可简单求解：

为了编写方便以下价格单位换算为千元。

sets：

u/1..4/;

m（u，u）：a，x;！x，招标矩阵，a，竞标价格矩阵;

endsets

data：

a=2 5 100 4.5

5 4 100 4

3 5 2 100

2 100 4 5;！100，很大数字表示不招标，不竞标;

enddata

min=1000？鄢@sum（m（i，j）：a（i，j）？鄢x（i，j））;

@for（u（i）： @sum（u（j）：x（i，j））<=2;

！每家公司至多可分配到2條线路;

@sum（u（j）：x（j，i））=1）;

@for（m（i，j）：@bin（x（i，j）））;

根据运行结果，公司1第1条线路中标，公司2第2条线路中标公司2第四条线路中标，公司3第3条线路中标，委员会的总花费最小，最小为12000.00元。

总之，数学实验的教学不仅需要教师熟练掌握数学理论知识，还要熟练掌握相关软件的使用，选择合适的教学内容，提高学生的学习兴趣，调动学生的积极性。希望在以后的数学教学中教师的教学水平逐步提高，学生的学习情况得到明显改善。

参考文献：

[1]托马斯·R·布莱克斯.右脑与创造[M].傅世侠译.北京：北京大学出版社，1993.

[2]孙云荪.数学实验[M].北京：科学出版社，1999.