大型环状压电振子的理论与实验研究

王笑竹，张 健

（营口理工学院 机电系，辽宁 营口 115014）

超声物料输送装置是从超声电机延伸出来的一种全新概念的新型驱动器，超声物料输送技术产业化的实现有赖于超声驱动原理的深入探讨[1-3].本文选择圆环形压电振子作为超声振动输送实验装置的换能器，设计并制作出试验用的多频变波长的超声输送实验装置，物料可以在环形“跑道”上做循环往复的无终点运动.旨在为超声输送速度等宏观输送性能的理论及实验研究提供测试平台.

1 振子结构设计和动态设计

超声物料输送装置的性能主要取决于振子的振动特性，因而振子设计在整个设计过程中是至关重要的.它主要包括振动模态设计、内外径的选择、振子厚度设计、齿的设计等几个方面.其中，模态分析是进行振子优化设计的有力工具，通过振子振动模态分析，可以不断修正振子的结构尺寸，从而找到符合要求的振型和相应的共振频率.换能器结构如图1所示.

圆环形压电振子在做面外弯曲振动时，同阶的两个弯曲模态，其频率差理论上为零，这对由圆环的两个同频弯曲驻波叠加为一个弯曲行波提供了设计上的便利，大量的数值计算与实验测试均表明，即使圆环上含有端面齿等复杂实体构造，其同阶弯曲模态的两个频率也十分接近，频率差几乎为零[4-5].圆环形输送振子的不利因素是物料的运行轨迹为圆弧线，离心力等因素对物料输送过程将产生额外作用.为减小这一不利影响，本文采用大型圆环压电振子结构，通过增大圆弧半径，改善曲率对物料输送性能的影响.

图1 换能器结构图

本文设计了一种多工作频率的超声物料输送装置，同一压电输送振子能在不同的工作模态下工作，为了检测输送装置在不同工作频率下的输送性能，在进行模态选择时，圆环形输送振子的固有频率不宜过高或过低，以防止出现因振幅太小或驱动点个数太少而造成的驱动力减弱的情况[6]；同时应保证同一输送振子的不同的工作模态所对应的固有频率之间有一定的频率差.以Bm，n表示振子的振动模态，m表示节圆数目，n表示节径数目.考虑到振子的B0，n模态，在相同的激励条件下，n越大，振子谐振频率就越大，振子越不易弯曲，本文选择压电振子的B0，11、B0，15弯曲振动模态作为工作模态.

压电振子由带有凸齿的圆环形弹性振子和粘贴在其底部的压电陶瓷环组成，分析中忽略振子金属圆环与压电陶瓷片之间胶接层的影响，把压电振子看成一个具有不同材料的固结体[7-8].利用ANSYS有限元软件分别调整振子内外径比r/R、振子厚度H、齿高ht、齿宽、压电陶瓷片厚度hp等参数使振子两个同阶弯曲模态频率差为零，并最终确定振子结构的具体尺寸如表1所示.

表1 圆环振子的主要结构参数

2 实验测试与分析

按照表1的结构参数，试制了行波型超声物料输送装置的圆环振子的3-3结构和圆环振子4-4结构.两振子陶瓷片的尺寸参数均为φ100 mm×φ80 mm×1 mm，为薄圆环形状.

对振子的振型、模态进行了测试，并根据测试结果分析讨论了振子模态正交性、驱动电压、工作频率与振幅关系以及径向质点振幅分布情况等内容.

实验过程中将压电陶瓷片不同分区进行了编号，编号分别为A、B、C、D（见图3），其中，A区和B区为压电振子B0，11阶弯曲模态对应的陶瓷片分区，即单独激励A区或者B区陶瓷片，将会激发出压电振子的B0，11阶驻波弯曲模态；C区和D区为压电振子的B0，15阶弯曲模态对应的陶瓷片分区，即单独激励C区或者D区陶瓷片，将会激发出振子的B0，15阶驻波弯曲模态.

测试时将频率设定在模态分析结果的数值上，在其附近调试，测得每组压电陶瓷片的谐振频率如表2、表3所示（激振电压峰值为80 V）.

图2 振子环的弯曲振动

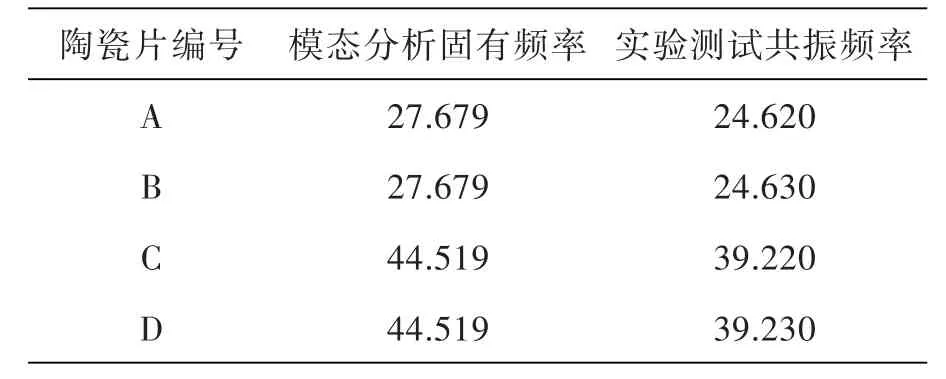
表2 3-3振子的谐振频率（单位：kHz）

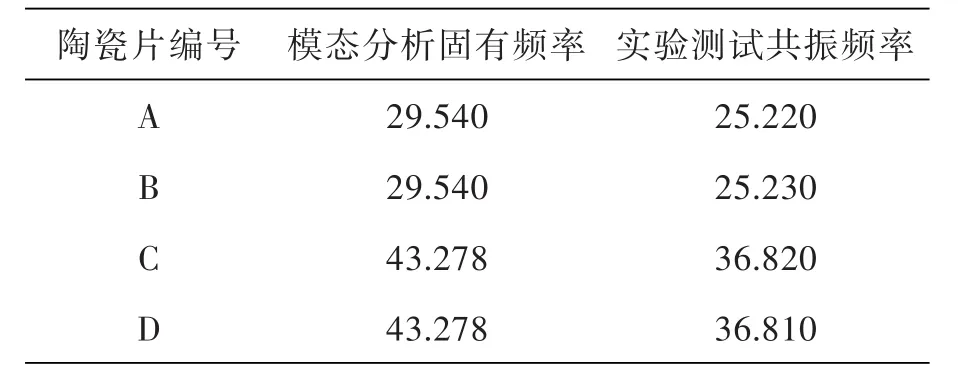
表3 4-4振子的谐振频率（单位：kHz）

2.1 振幅分布情况

振幅分布测试从做标记的齿位置开始测试，第一次测试在齿的中央位置，让每次的测试点均在齿面上.

以频率为24.62 kHz（39.22 kHz）的正弦信号分别激励3-3振子的A组、B组（C组、D组）压电陶瓷片（激振电压峰峰值为80 V），测得振子表面质点的振幅分布情况如图5（a）、图5（b）所示（每次测试的测试点相同），图中实线为激励B（C）组压电陶瓷片时质点的振幅分布情况，虚线为激励A（D）组压电陶瓷片时质点的振幅分布情况.

从图5可以看出，实线与虚线的分布规律几乎相同，二者之间存在一个相位差，这是由两组压电陶瓷片之间相差1/4波长所致，两条曲线一个模态中的峰值点为另一个模态的零点，可见，实验测得的振子同阶的两个弯曲模态符合同频正交这一特性.另外，图5所示的两条曲线出现了极值点振幅明显不等的现象，这是由于两组压电陶瓷片性能上的差异造成的.

同理，激励电压（80 V）保持不变，以频率为25.22 kHz的正弦信号激励4-4振子的A组压电陶瓷片，对振子表面质点的振幅分布进行测试，得到振幅分布如图6（a）中实线所示；再以25.22 kHz的正弦信号激励4-4振子的B组压电陶瓷片，测试得到振子表面质点的振幅分布规律如图6（a）中虚线所示（测试点与激励A组压电陶瓷片时的测试点相同）.与图5所示的振幅分布规律相同，两条曲线也出现了极值点振幅明显不相等的现象.

利用上述实验方法，以频率为36.82 kHz的正旋信号激励4-4振子的C组压电陶瓷片，对振子表面质点的振幅分布进行测试，得到振幅分布如图6（b）中虚线所示；再以36.82 kHz的正旋信号激励4-4振子的D组压电陶瓷片，测试得到振子表面质点的振幅分布规律如图6（b）中实线所示（测试点与激励C组压电陶瓷片时的测试点相同）.

图3 圆环振子

图4 模态测试信号流程图

从图5、图6可以看出：B0，11阶弯曲振动对应的每条曲线的波峰与波峰（波谷与波谷）之间都约为16.4°，等于1/2波长（λ0，11/2）对应的角度，并且同一图中，两相驱动对应曲线的波峰与波峰（波谷与波谷）之间都约为8.2°，等于1/4波长（λ0，11/4）对应的角度. 同样，从图5、图6看出：B0，15阶弯曲振动对应的每条曲线的波峰与波峰（波谷与波谷）之间都约为12°，等于1/2波长（λ0，15/2）对应的角度，并且同一图中，两相驱动对应曲线的波峰与波峰（波谷与波谷）之间都约为6°，等于1/4波长（λ0，15/4）对应的角度.因此，可以证明实验测得的振子模态与有限元软件分析结果一致.

图5 3-3振子振幅分布曲线

图6 4-4振子振幅分布曲线

2.2 驱动电压与振幅的关系

在其他条件保持不变的情况下，对驱动电压与振子表面质点的振幅分布关系进行了测试.以3-3振子的B0，15阶弯曲模态为例，以频率为39.22 kHz的正弦信号激励振子的D组压电陶瓷片，使驱动电压在30～200 V范围内变化，步长为10 V，测得振子表面某一质点振动的振幅与驱动电压的关系如图7所示，图中曲线表明，在工作频率保持恒定的情况下，振幅随驱动电压的增大呈线性增加.

图7 驱动电压-振幅的关系曲线

2.3 工作频率与振幅关系

在激励电压固定的情况下，调节输入信号的频率，使振子的激振频率在谐振频率附近变化，调整步长为10 Hz，测试振子表面质点振幅随频率的变化曲线.测试结果如图8（a）、（b）所示. 其中左列图为振子的B0，11阶弯曲模态下的幅频特性曲线，右列图为B0，15阶弯曲模态下的幅频特性曲线.从曲线可以看出：在谐振频率下，振子表面质点振动的振幅达到最大.

图8 工作频率与振幅关系图

2.4 径向质点振幅分布

本节将对同一半径上不同质点的振幅分布情况进行实验测试.本文设计的环形振子宽度为10 mm，在该宽度方向上每1 mm选取一测试点，以距离圆心位置最近的点为起点，对上述10个测试点从1到10进行编号.以驱动电压为80 V、激振频率为39.22 kHz的正弦信号激励3-3振子的C组压电陶瓷片，对所选取的上述10个测试点的振幅分布进行实验测试，测试结果如图9所示.从曲线可以看出，柱坐标下相同θ坐标质点的振幅随极径坐标r的增大而增大.

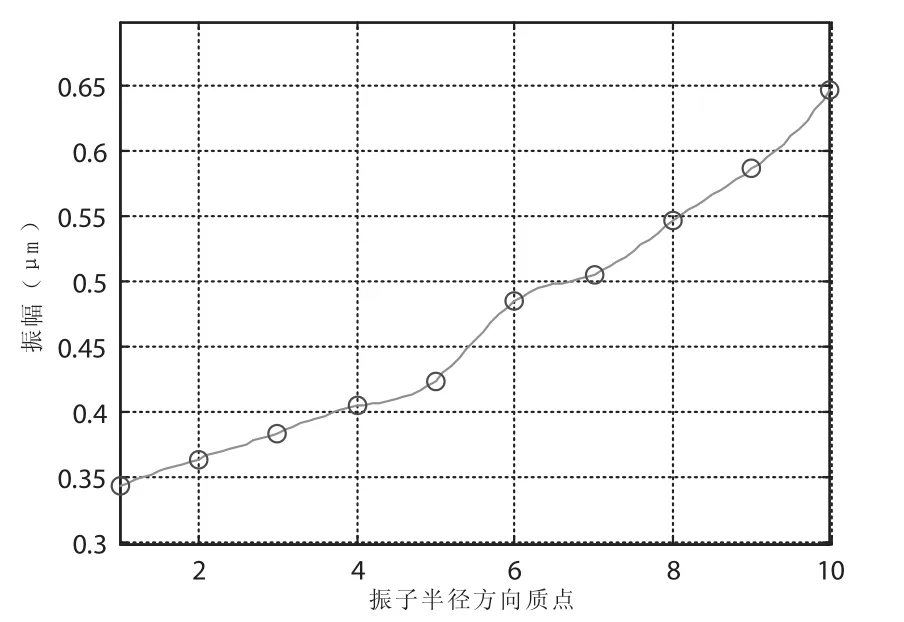
图9 半径方向质点的振幅分布

3 结论

利用ANSYS有限元分析软件对环形输送振子的结构进行了动态设计，确定了振子的结构尺寸参数，并优选出振子的B0，11、B0，15阶弯曲模态及对应的固有频率. 通过对压电陶瓷片的分区极化设计，实现了同一压电振子在多阶弯曲模态即多工作频率下的驱动.基于理论分析结果，制作了环形输送装置的原理样机.对振子表面质点的振幅分布特性进行了实验测试.实验结果表明：在激振频率一定的情况下，振子表面质点的振幅随驱动电压的增大呈线性增大；在驱动电压一定的情况下，质点振幅在振子达到谐振时达到最大；位于同一半径上的质点的振幅随极径坐标的增大而增大.对输送装置不同工作模态下的输送性能进行了实验测试.测试结果表明：本文所设计的超声物料输送装置在不同的工作模态下均具有较好的输送能力、均能平稳地输送物料，并且在一定范围内可调；在振子表面质点的最大振幅为1μm、驱动频率分别为24.69 kHz及 39.31 kHz的实验工况下，输送装置的 B0，15、B0，11阶工作模态对应的输送速度比为定值，并且实验测试结果与理论分析值一致.

[1]赵淳生.超声电机技术与应用[M].北京：科学出版社，2007：158-159.

[2]于跃.基于郎之万振子的直线式超声波振动给料系统的研究[D].吉林：吉林大学，2008.

[3]胡敏强，金龙，顾菊平.超声波电机原理与设计[M].北京：科学出版社，2005：203-206.

[4]李静.旋转型驻波超声电机的理论与实验研究[D].锦州：辽宁工业大学，2008：25-28.

[5]何勍，董瑞芳，王宏祥.块体物料超声输送能力测试实验装置的研究[J].压电与声光，2010，32（1）：145-148.

[6]何勍，王丹妮，王宏祥.环形压电振子面内弯曲模态特征及控制[J].压电与声光，2010，32（4）：585-587.

[7]MRACEK M,WALLASCHEK J.A system for power transport based on piezoelectrically excited ultrasonic progressive waves[J].Materials Chemistry and Physics,2005,90(2):378-380.

[8]陈超，曾劲松，赵淳生.行波超声电动机的动力学模型[J].机械工程学报，2006，42（4）：76-86.