双重逆极限空间上移位映射的Li－Yorkeτ混沌

罗 飞

（重庆师范大学 数学学院，重庆401331）

1 双重逆极限空间的定义

以下定义请参考文献［1］和［2］.

设X非空紧致度量空间，f：X→X，g：X→X都是连续映射且满足f◦g＝g◦f，记集合显然（其中Xi，j＝X，∀i，j∈Ζ）.以后把X 中的点都简记为 （xi，j）.在上引入度量：

σf◦σg是上的同胚映射，并称之为由f◦g诱导出来的上的移位映射.由于f◦g＝g◦f，故同样有σf◦σg＝σg◦σf.

2 Li－Yorkeτ混沌

设f，g为X上的连续映射，且f◦g＝g◦f，设τ≥0，存在不可数集C⊂X，称f◦g是Li－Yorke τ意义下混沌，如果f◦g满足：

则称这样的集C为f◦g的混沌集，f◦g是Li－Yorkeτ混沌的.

定理1 设f，g为紧致度量空间上的连续满射，且f◦g＝g◦f，则σf◦σg是Li－Yorkeτ意义下混沌的当且仅当f◦g是Li－Yorkeτ意义下混沌的.

证 首先设f◦g是Li－Yorkeτ意义下混沌的，C⊂X是f◦g的一个不可数混沌集，并且xi，j，yi，j∈C，xi，j≠yi，j，对τ≥0有

对于每一个xi，j∈C取定）中的一个元素记为，令由C 是不可数集可知T也是不可数集.

下面证明T为σf◦σg的一个混沌集.

又因为

其中M＞0为紧致度量空间X上的直径.则当k，h＞K时

另一方面，假设σf◦σg是Li－Yorkeτ意义下混沌的，T是σf◦σg的一个混沌集.

对于 ∀xi，j，yi，j∈C，对任意的使

不失一般性可以进一步假设，si＜ni＜si＋1＜ni＋1，ti＜mi＜ti＋1＜mi＋1.对于每一个i＞0，有

（ki，hi）＝ max｛（n，m）：n＜ni，m ＜mi且则有si≤ki＜ni，ti≤hi＜mi.

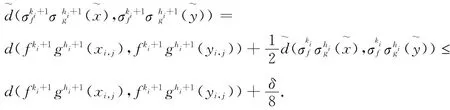
因此C是f◦g的一个混沌集.

［1］顾荣宝.逆极限空间上移位映射的拓扑熵与混沌［J］.武汉大学学报：自然科学版，1995，41（1）：22－26.

［2］蒋达锋.双重逆极限空间上的动力性质［D］.苏州大学，2005.

［3］周作岭.符号动力系统［M］.上海：上海科技教育出版社，1997.

［4］陈绥阳，褚蕾蕾.动力系统基础及其方法［M］.北京：科学出版社，2002.

［5］张筑生.微分动力系统原理［M］.北京：科学出版社，2003.