三角模糊数型模糊多属性群决策方法

顾翠伶，梁艳艳，张 茜

（周口师范学院 数学与统计学院，河南 周口466001）

多属性决策问题的实质是利用已有的决策信息通过一定的方式对一组有限个备选方案进行排序并择优.多属性决策是现代决策科学的核心内容之一，它广泛应用于社会、经济、管理等多个领域中.群决策可以弥补单个决策者知识结构和经验水平的局限性，在管理决策中能更好地处理决策问题，提升决策质量，近年来，已有大量关于模糊多属性（群）决策分析方法的研究［1－9］.其中文献［1］针对只有部分属性权重信息且属性值以区间数形式给出的不确定多属性决策问题，提出一种逼近理想关联度的决策分析方法.文献［3］针对方案的属性评估信息和属性权重是模糊语言形式的多属性群决策问题，将语言信息转化为三角模糊数，利用三角模糊数的性质，构造集结决策者权威性和意见一致性的组合一致性指标，并给出一种模糊多属性群决策算法.曾三云［6］针对属性值为模糊变量，属性权重完全未知但已知方案优先序的模糊多属性决策问题给出新的决策方法.该方法通过建立一个线性目标规划模型来确定属性的权重，再基于简单加权平均法则来计算各方案的模糊综合属性值，然后根据比较模糊变量大小的期望值方法对方案进行排序.胡丽芳［9］对模糊群体多属性决策问题，依据一般的灰色关联分析方法的基本思路，将灰色关联度和欧氏距离结合，构造平均相似度对方案进行评价，提出一种新的灰色多属性决策方法.

在决策过程中，由于决策时间、专家知识结构等的限制，决策专家对于方案或者属性的认识的不深刻等，这样就要求给决策专家一个权重以区别专家的重要性.笔者给出一种确定专家权重的方法，将语言值模糊信息化为三角模糊数形式，利用三角模糊数的模，将决策群体中每个专家的权重精确化.熵度量方案的模糊性，方案的熵越大，模糊性越强，方案就越劣.方案的散度面积越大，可行域也越大，方案越优.贴近度度量两个模糊数之间的贴近程度，贴近度越大，说明两个模糊数越接近.决策方案与正理想方案的贴近度越大，与负理想方案的贴近度越小，方案越优.本文融合模糊熵、散度面积以及方案与正、负理想方案之间的海明贴近度，给出排序方案的综合指标值，该综合指标值越大，方案越优.最后给出一个具体的算例分析，验证该方法的合理性和有效性.

1 预备知识

定义1［10］一个模糊数A定义为fA：R→I＝ ［0，ω］的模糊集，满足

（1）fA是上半连续的；

（2）存在一个区间 ［a，d］，当x∉ ［a，d］时，有fA（x）＝0；

（3）存在实数b，c满足a≤b≤c≤d ，fA（x）在 ［a，b］单调递增；fA（x）在 ［c，d］上单调递减；fA（x）＝1在［b，c］上.即隶属函数可以表示为：

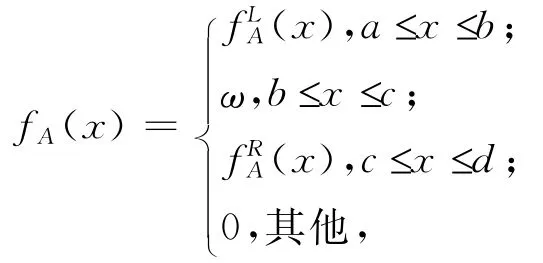
定义2［11］一个模糊数A的参数形式为分别为的反函数（0≤r≤1）.且（r）与（r）满足下列要求：

定义3 称

为模糊数A的权重面积，且有S（A）越大越好.这里将此权重面积作为模糊数散度的一个衡量指标.可见模糊数的权重面积越大，散度越大，可行域也就越大.

对一组模糊数 ｛A1，A2，…，An｝，定义

则s（Ai）越大，模糊数越优.

定义4［12］假设A为连续模糊变量，则其熵定义为

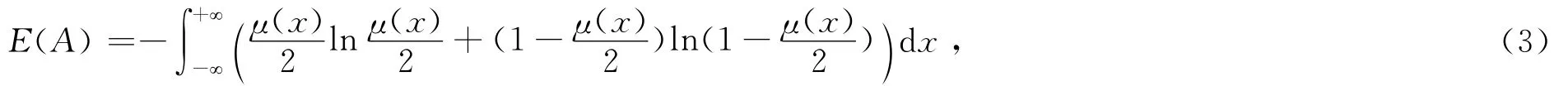
模糊变量的熵值越大，模糊性就越强，模糊变量就越劣.

对于一组模糊变量 ｛A1，A2，…，An｝，定义

e（Ai）越大，模糊变量越劣.

定义5［13］令A、B和C为论域X 中的模糊集合，若映射σ：F（X）×F（X）→ ［0，1］具有性质：

（1）σ（1，1）＝1；

（2）σ（A，B）＝σ（B，A）；

（3）由A⊇B⊇C或A ⊆B⊆C可得σ（A，B）≥σ（A，C），则称σ（A，B）为A与B的贴近度.

贴近度的性质（1）说明两个相同的模糊集合的贴近度最大，性质（2）要求贴近度具有对称性，而性质（3）描述了两个接近的模糊集合的贴近度也较大.

定义6［13］海明贴近度：

2 模糊多属性决策方法

与经典多属性决策相类似，模糊多属性决策基本模型可以描述为：给定一个方案集A＝｛A1，A2，…，Am｝，和相应于每个方案的属性集C＝｛C1，C2，…，Cn｝，以及说明每种属性相对重要程度的权集ω＝｛ω1，ω2，…，ωn｝，决策专家群体为Z＝ ｛Z1，Z2，…，Zl｝.其中，关于属性指标和权值大小的表示方式可以是数字的，也可以是语言的；涉及的数据结构可以是精确的，也可以是语言的；涉及的数据结构可以是精确的，也可以是不精确的.而所有语言的或不精确的属性指标，权值大小和数据结构等都被相应地表示成决策空间中的模糊子集或模糊数.

Step1 决策矩阵标准化

假设每个专家Zk对方案的评价矩阵

由于不同的评价属性通常具有不同的物理量纲和量纲单位，且不同的量纲和量纲单位会带来不可公度性，因此在决策之前应将属性进行无量纲和规范化处理［9］.

设S＋为效益型指标，S－为成本型指标，可以按照下列公式将属性决策矩阵Qk转化为规范化矩阵Rk

所以有

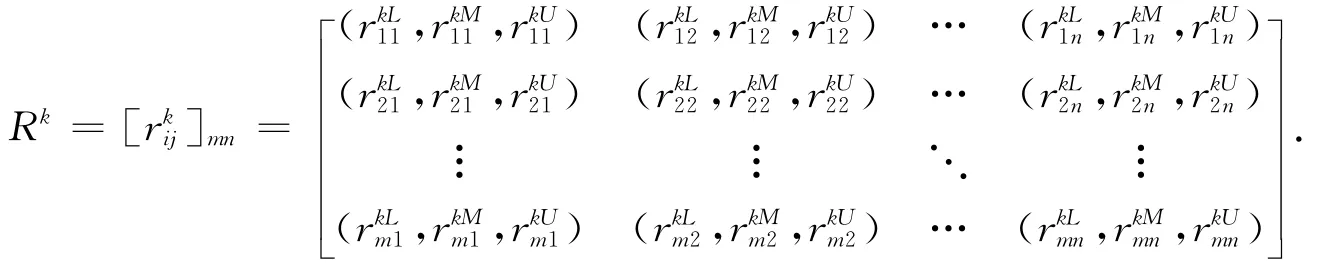
Step2 求群体决策矩阵

在专家组成的团队里，有些专家的意见很重要，而另外一些专家的意见相对来说不是那么重要，这样就要求给各专家一个权重.每个专家的意见我们以语言形式给出，将语言形式转化为三角模糊数，对应表如下：

表1 语言评估标度与三角模糊数

若有l个专家，每个专家的权重以模糊语言值的形式给出，根据模糊语言值与模糊数的对应表（表1），则专家模糊权重信息值.将模糊权重去模糊化，得到专家的精确权重.

定义第k个专家对应的精确权重为

求出每个专家的权重，根据各个专家对不同方案关于属性值的决策矩阵，得到群体决策矩阵

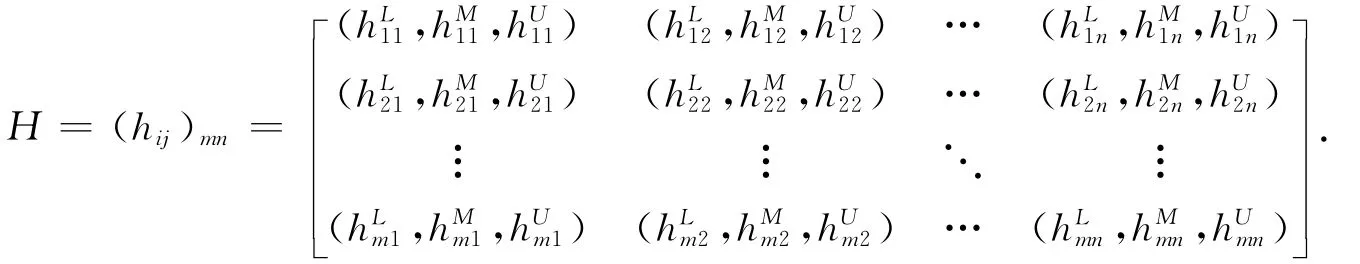
其中

Step3 确定正理想方案和负理想方案

求专家群体决策矩阵的正、负理想方案.

Step 4 求方案与正、负理想方案间的贴近度

根据公式（5）可以求得各个方案属性值与正、负理想方案属性值之间的海明贴近度与从而第i个方案与正理想方案的贴近度为αj为第j个属性的权重值，并且

第i个方案与负正理想方案的贴近度.因为方案与正理想方案的贴近度越大，同时方案与负理想方案的贴近度越小，方案越优.所以综合方案与正、负理想方案之间的贴近度信息，给出如下的指标：

其中ρ为决策者群体偏好，代表决策专家对正负理想方案的偏好程度.φi越大，方案越优.

Step5 计算各个方案的模糊熵与散度指标

根据属性权重信息及专家群体决策矩阵可以得到每个方案的综合评价值：

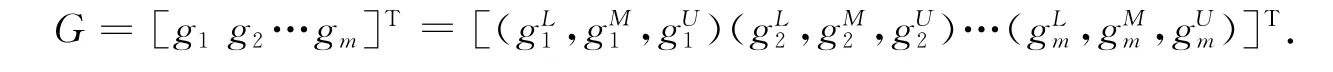
其中

根据公式（1）、（3）得第i个方案的散度值S（gi）、熵值E（gi），根据公式（2）、（4）求得各个s（gi）与e（gi）.

Step6 求各个方案的综合排序指标值

结合方案的熵信息、散度指标以及各方案与正、负理想方案之间的贴近度，得到每个方案的综合排序指标φi越大，方案越优.

3 实例分析

某生产公司进行新厂址选址，有四种可供选择的方案X1，X2，X3，X4，属性指标值有三个ζ1，ζ2，ζ3，假设三个指标均为效益型指标.专家群组为Z1，Z2，Z3，每个专家关于决策方案的属性评价值由三角模糊数给出.

确定模糊决策矩阵：

将模糊决策矩阵标准化：

三位专家Z1，Z2，Z3分别为特别重要，很重要，一般重要，根据表1，三位决策专家的模糊权重用三角模糊数表示为：

由公式（6）则三位专家的权重为：

结合专家的权重，求出群体决策矩阵：

求正负理想方案：

确定各个方案与正负理想方案的贴近度，假设这里三个属性指标的权重分别为0.43，0.36，0.21.

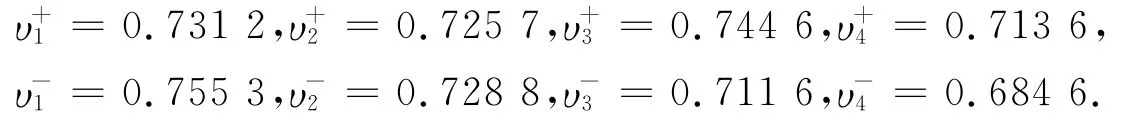
根据公式（7）可以求得

根据三个属性的权重值与专家群体决策矩阵可以得到每个方案的评价值：G ＝ ［g1，g2，g3，g4］T＝ ［（0.14，0.29，0.63）（0.16，0.30，0.69）（0.15，0.31，0.67）（0.13，0.31，0.72）］T.

根据公式（1）、（2）、（3）、（4）计算得到

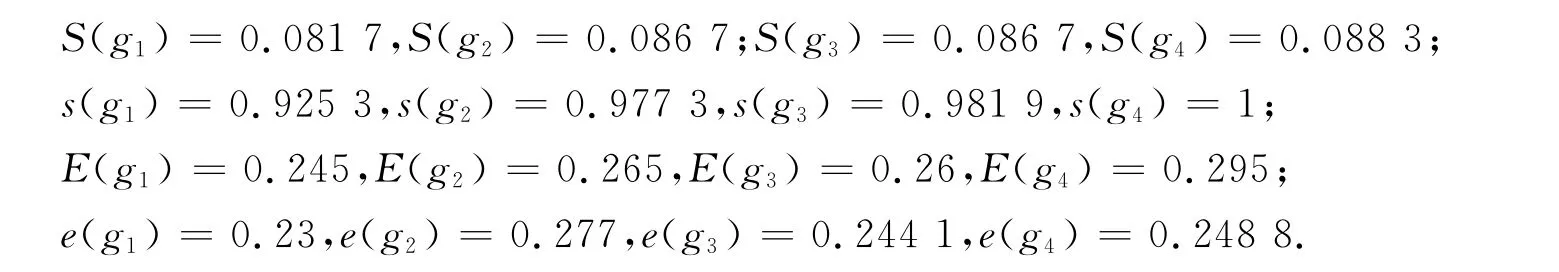
利用公式（8）得到每个方案的综合评价值

φ1＝0.780 2，φ2＝0.778 0，φ3＝0.769 3，φ4＝0.759 2，因而最优的方案为X1.

4 总结

笔者针对决策信息、属性权重为三角模糊数的模糊多属性群决策问题，利用方案与正、负理想方案之间的贴近度，融合方案的熵值信息、散度信息，提出一种新的排序方案的综合指标；同时，依据语言评价信息，将专家的语言权重信息转化为三角模糊数形式.给出一种新的解决模糊多属性群决策问题的方法.实例分析，验证了所述方法的合理与有效性，但是对于模糊多属性决策问题仍存在需要深入研究的问题，比如各种求解模糊多属性决策方法的比较等问题.

［1］冯向前，魏翠萍，李宗植.基于理想关联度的不确定多属性决策方法［J］.运筹与管理，2007，16（2）：24－29.

［2］周晓光，张强.基于 Vague集的群决策方法研究［J］.数学的实践与认识，2007，37（19）：12－18.

［3］陈晓红，阳曦.一种基于三角模糊数的多属性群决策方法［J］.系统工程与电子技术，2008，30（2）：278－288.

［4］戴厚平.基于模糊数直觉模糊集的多属性决策方法［J］.模糊系统与数学，2013，27（2）：149－154.

［5］郭欣.基于改进的信息熵为权重的模糊多属性决策［J］.中国科教创新导刊，2013，26：22－24.

［6］曾三云.带有方案优先序的模糊多属性决策方法［J］.模糊系统与数学，2013，27（1）：132－136.

［7］何霞，刘卫锋.一种有方案偏好的直觉模糊多属性决策方法［J］.运筹与管理，2013，22（1）：36－40.

［8］彭展声，农秀丽.模糊多属性决策的最小偏差法［J］.统计与决策，2009，6：156－157.

［9］胡丽芳，关欣，何友.一种新的灰色多属性决策方法［J］.控制与决策，2012，27（6）：895－898.

［10］Abbasbandy S，Asady B.Ranking of fuzzy numbers by sign distance［J］.Information Sciences，2006，16：2045－2416.

［11］Ma M，Friedman M，AKandel.A new fuzzy arithmetic［J］.Fuzzy Set and Systems，1999，108：83－90.

［12］Liu B D.Uncertainty theory：an introduction to its axiomatic foundations［M］.Berlin：Springer，2004.

［13］蒋泽军.模糊数学教程［M］.北京：国防工业出版社，2010.