浅水波方程的周期波解

傅海明，戴正德

（1.广州华夏职业学院 基础部，广东 广州510935；2.云南大学 数学与统计学院，云南 昆明650091）

随着科学技术的发展，非线性科学在自然科学、社会科学等领域中的应用越来越广泛，特别是寻找非线性发展方程的精确解在非线性的问题研究中占有重要地位.传统的求解非线性发展方程的方法主要有逆散射法［1］、Backlund法［2］、Darboux变换法［3］、Hirota双线性法［4－5］、Painlevé展开法［6］等.近年来，涌现出一系列新的求解方法，如齐次平衡法［7］、双曲正切函数展开法［8］、包络变换法［9］、利用分支理论直接积分的方法［10］、F－方法［11－12］等.

本文利用扩展了的Hirota法得到浅水波方程

的新的周期波解.下面，给出具体方法及步骤.

设

引进双线性算子

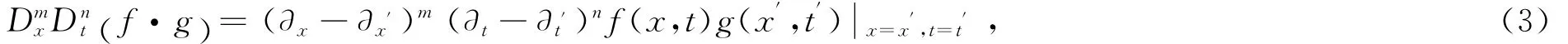
利用式（2），（3）把方程（1）写成如下双线性型

令

其中，ξi＝kix＋wit（i＝1，2，3，4）.把式（5）代入式（4），令sinξiexp（jξ4），cosξiexp（jξ4），sinhξ3exp（jξ4），coshξ3exp（jξ4），exp（0），i＝1，2；j＝－1，1的系数为零得

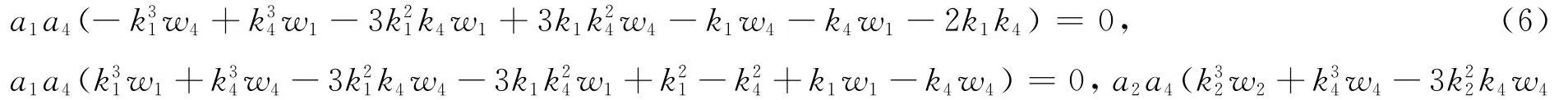
解以上方程组，得

（1）当a4＞0时，令ξ0＝ln.把式（7）和式（5）代入式（2）得到方程（1）的解为

图1 u1的图像

取a2＝1.2，a4＝4，k2＝2，k4＝0.4，w2＝0.8，w4＝1.2时，u1的图像见图1.

（2）当a4＜0时，令.把式（7）和式（5）代入式（2）得到方程（1）的解为

（1）当a4＞0时，令.把式（8）和式（7）代入式（2）得到方程（1）的解为

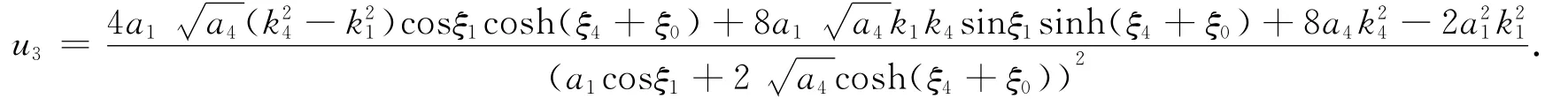
取a1＝1.8，a4＝2，k1＝1.8，k4＝1.2，w1＝1.6，w4＝0.4时，u3的图像见图2.

（2）当a4＜0时，令把式（8）和式（7）代入式（2）得到方程（1）的解为

取a1＝0.2，a4＝1.8，k1＝0.9，k4＝1.5，w1＝1.6，w4＝0.01时u4的图像见图3.

图2 u3的图像

图3 u4的图像

本文扩展了Hirota法，即将Hirota法中的测试函数用新的测试函数来替代.以浅水波方程为例，给出用这个扩展后的方法求孤波解的具体过程，这些周期解是新的.容易看到，这个扩展后的方法适用于相当一部分非线性发展方程.

［1］ABLOW ITZ M J，CLARKSON P A.Soliton，nonlinear evolution equations and inverse scattering［M］.Cambridge：Cambridge Univ.Press，1991.

［2］谷超豪.孤立子理论及其应用［M］.杭州：浙江科技出版社，1990.

［3］MATVEEV V B，SALLEM A.Daroux transformations and solitons［M］.Berlin：Springer，1991.

［4］HIROTA R.Exact solution of the Korteweg－de Vries equation for multiple collisions of solitons［J］.Phys Rev lett，1971，27：1192－1194.

［5］傅海明，戴正德.（3＋1）维孤子方程的周期孤波解［J］.东北师范大学学报：自然科学版，2011，43（1）：16－19.

［6］楼森岳.推广的Painlevé展开及 KdV方程的非标准截断解［J］.物理学报，1998，47：1739－1745.

［7］Haiming F U.Exact Solutions for a class of Variable Coefficients Nonlinear Evolution Equations［J］.Modern Applied Science，2008，2（5）：34－36.

［8］李志斌，张善卿.非线性波方程准确孤立波解的符号计算［J］.数学物理学报，1997，17（1）：81－89.

［9］傅海明，戴正德.一个（2＋1）－维激光方程的孤波解［J］.西北师范大学学报：自然科学版，2009，45（1）：44－47.

［10］LI JIBIN，ZHANG LIJUN.Bifurcations of traveling wave solution in generalized Pochhammer－Chree equation［J］.Chaos，Soitons and Fractals，2002，14：581－593.

［11］FAN E G.Travelling wave solutions in terms of special functions for nonlinear coupled evolution systems［J］.Physics Letters A，2002，300：243－249.

［12］傅海明，戴正德.Kadomtesv－Petviashvily方程的新解［J］.四川师范大学学报：自然科学版，2011，34（1）：77－79.