集值优化问题Proximal真有效解集的连通性

李小燕，岳瑞雪

（重庆师范大学 数学学院，重庆401331）

在向量优化问题中，首要的问题是如何定义解.1951年，Koopmans［1］在生产与分配的活动分析中首次引进了Pareto有效点的概念.然而，一些有效点并不具备标量化特征，为了避免这种情形，各种真有效点的概念被引入.如，Kuhn－Tucher［2］首次引进的 Kuhn－Tucher真有效点、Geoffrion［3］真有效点、Browein［4］真有效点、Benson［5］真有效点以及Borwein和Zhuang［6－7］在赋范空间中定义的超有效点（解）的概念等.

2005年，Lalitha和Ruchi Arora［8］利用Proximal法锥就向量优化问题又提出了一种新的真有效点的概念，称之为Proximal真有效点.而对真有效点集和真有效解集的连通性研究也是向量优化理论中十分重要的课题.许多学者对真有效解集的连通性进行了研究，并取得了大量的研究成果［9－12］.本文首先研究了集合的Proximal真有效点的连通性，其后讨论了集值优化问题Proximal真有效解集的连通性.

1 预备知识

设C⊂RP，若对任意的c∈C，λ≥0，λ∈R，有λc∈C，则称C为锥.若C∩－（）C⊂｛｝0，则称C为点集，C的严格正极锥定义为

C的正极锥定义为

本文总假设A为Rp中的闭集，C为Rp中的闭凸点锥.∈A称为A关于C的有效点，如果关于 的有效点之集记为 ，C Eff ［AC］.

定义1［13］令x∈RP，∈A为x在A上的投影，即｜｜｜｜＝min｜｜a｜｜.∀λ≥0，a∈A向量λ（x －）称为A在的Proximal法向量.所有法向量之集称为A在的Proximal法锥，记为NP（A ，），x在A上的投影之集记为projA（x）.假设a∈A，且对∀x∉A都有a∉projA（x），则令NPA，（）a＝｛｝0.

定义2［8］称点∈A为集合A的Proximal真有效点，如果

A的Proximal真有效点之集记为Pr［A，C］.

引理1 设φ∈C＊0，记SφA ＝ ｛∈A｜φ·＝inf｛φ·a｜a∈A ｝｝，D ［A，C］＝∪φ∈C＊0SφA，若A＋int C凸，则Pr［A，C］＝D［A，C］.

设S⊆Rp且S非空，Y＝Rp.考虑如下集值优化问题：

其中，F：S→2Y为集值映射.记（）F S＝∪x∈S（）F x.

定义3［8］∈S称为（）VP的Proximal真有效解，如果

（VP）的所有Proximal真有效解之集记为PE［F，C］.

设φ∈C＊0，记

定义4［14］设S是非空凸集，C是Y中的闭凸锥，F：S→2Y为集值映射，称F在S上是C－凸的，若对任意的x1，x2∈S，λ∈ （0，1）有

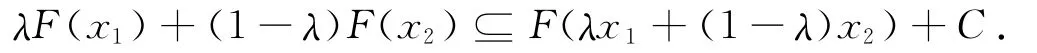
2 主要结果

定理1 若F在C上是C－次类凸的，即F （S）＋int C是凸集，则

Pr［F （S），C］＝D［F （S），C］，所 以F （）∩ D ［F （S），C］≠ ∅ ，则存在即存在使得，那么所以

引理2［15］设S是连通集，F：S→2Y为上半连续集值映射，且对任意的x∈S，（）F x是Y中的连通集，则∪x∈S（）F x是Y中的连通集.

定理2 若A为紧凸集，则Pr［A，C］为连通集.

证 由引理1有Pr［A，C］＝D［A，C］.首先证明SφA 为凸集.事实上，任取a1，a2∈SφA，λ∈ （0，1），有φ·a1＝ φ·a2＝inf｛φ·a｜a∈A ｝，由 A 为凸集，有λa1＋ （1－λ）a2∈A.所以φ［λa1＋ （1 －λa2）］＝λφ·a1＋ （1－αλ）φ·a2＝inf｛φ·a｜a∈A ｝，所以λa1＋ （1 －λa2）∈SφA .因此SφA为凸集.再证H：C＊0→2A，其中H（φ） ＝SφA，在C＊0上上半连续.假设H在某处不上半连续.则存在开集O⊇H（），｛φn｝⊆C＊0，φn→，使得H（φn）⊄O，即存在an∈H（φn），使得

由an∈H（φn），有

因为A为紧集，不失一般性，设an→∈A，则φn·an→·.由 （1）有·≤·a，∀a∈A.所以∈H（）⊆O，因此∈O.又由O为开集及an→有，当n充分大时有an∈O，这与an∉O矛盾.因此H在C＊0上上半连续.最后，易证C＊0为凸集.因此，由引理2有Pr［A，C］为连通集.

注1 若定理中的条件不成立，则结论不一定成立，见如下例子.

定理3 设S是非空紧凸集，C⊆Y为闭凸锥，F：S→2Y在S上是上半连续的，且对任意的x∈S，F （x） 是紧集.若F在S上是C－凸的，则PE［F，C］为连通集.

证 由定理1有PE［F，C］＝∪φ∈C＊0B ［F ，φ］ .先证B ［F ，φ］ 为非空凸集.事实上，因为S非空紧，F在S上上半连续，且对任意的x∈S，F （x）是紧集，所以F （S）是紧集，因而B ［F ，φ］ 非空.下证B ［F ，φ］ 是凸集.任取x1，x2∈B ［F ，φ］ ，λ∈ （0，1），则存在y1∈F （x1），y2∈F （x2），使得φ·F （S）＝φ·y1＝φ·y2.因为F在S上是C－凸的，则存在使得λy1＋ （1－λ）y2从而有因此所以minφ·，因此，λx1＋（1－λ）x2∈B ［F ，φ］ ，所以B ［F ，φ］ 是凸集.令H：C＊0→2S，其中H（φ） ＝B ［F ，φ］.

下证H在C＊0上上半连续.假设H在某处不上半连续.则存在开集使得H（φn）⊄O，即存在sn∈H（φn），使得sn∉O，∀n.

由sn∈H（φn），有minφn·F （S）∈φn·F （sn）.即存在yn∈F （sn），使得yn＝minφn·F （S）.因S为紧集， F在S上上半连续，且对任意的x∈S，F （x）是紧集，因此，F （S）是紧集，不失一般性，设则从而因F在S上上半连续，则，从而即，这与 矛盾sn∉O.

因此H在C＊0上上半连续.最后，易证C＊0为凸集.则由引理2有PE［F，C］为连通集.

［1］T C Koopmans.Analysis of production as an efficient combination of activities［C］.In：T.C.Koopmans，Activity Analysis of Production and Allocation.Cowles Commission Monograph.New York：John Wiley and Sons，1951，13：33－97.

［2］H W Kuhn，A W Tucker.Nonlinear programming［C］.In：proceeding of the Second Berkeley Symposium on Mathematical Statistics and Probability（University of California Press，Berkeley，CA），1951：481－492.

［3］A M Geoffrion.Proper Efficiency and the theory of vector maximization［J］.J.Math.Anal.Appl.，1968，22：616－630.

［4］J M Borwein.Proper Efficient Points for maximizations with respect to cones［J］.SIAM J.Control and Optim，1997，15：57－63.

［5］H P Benson.An improved version of proper efficiency for vector minimization with respect to cones［J］.J.Math.Anal.Appl.，1979，71：232－241.

［6］J M Borwein，D M Zhuang.Super efficiency in convex vector optimization［J］.ZOR－Methods Models Oper.Res.，1991，35：175－184.

［7］J M.Borwein，D M Zhuang.Super efficiency in vector optimization［J］.Amer.Math.Soc.，1993，338：105－122.

［8］C S Lalitha，Arora Ruchi.Proximal proper efficiency for minimisation with respect to normal cones［J］.Bull.Austral.Math.Soc.，2005，71：215－224.

［9］X H Gong.Connectedness of super efficient solution sets for set－value maps in Banach spaces［J］.Mathematical Methods of Operations Research，1996，44：135－145.

［10］W D Rong，Y N Wu.Characterizations of super efficiency in cone－convexlike vector optimization with set－valued maps［J］.Mathematical Methods of Operations Research，1998，35：247－258.

［11］X Y Zheng.Proper efficiency in locally convex topological vector spaces［J］.J.Optim.Theory and Appl，1997，94：469－486.

［12］凌晨.赋范线性空间中锥拟凸向量优化问题超有效解集的连通性［J］.数学研究与评论，2002，22（1）：103－106.

［13］F H Clarke，Y S Ledyaev，R J Stern，et al.Nonsmooth analysis and control theory［M］.New York：Springer Verlag，1998.

［14］Z F Li.Benson Proper Efficiency in the Vector Optimization of Set－valued maps［J］.Journal of Optimization Theory and Applications，1998，98（3）：623－649.

［15］胡毓达，胡一凡.锥拟凸与拓扑向量空间多目标最优化有效解集和弱有效解集的连通性［J］.应用数学学报，1989，12（1）：115－123.