光刻机运动平台系统的模型辨识
2015-06-15范文超陈兴林
范文超 陈兴林 王 斌 魏 凯
(哈尔滨工业大学航天学院,黑龙江 哈尔滨 150001)
光刻机运动平台系统的模型辨识
范文超 陈兴林 王 斌 魏 凯
(哈尔滨工业大学航天学院,黑龙江 哈尔滨 150001)
针对机械谐振对超精密光刻系统的影响,对包含有机械谐振的光刻机宏微运动平台进行辨识来抑制机械谐振。首先建立单自由度宏微耦合运动模型和谐振模型,然后基于递阶辨识原理对机械谐振模型进行分段辨识,最后基于谐振模型设计陷波器,抑制机械谐振。试验结果证明,该方法有效抑制了宏微平台的机械谐振,大幅提高了系统的动态响应性能。
光刻机 宏微耦合模型 机械谐振 递阶辨识 动态响应性能
0 引言
近年来,随着半导体加工领域的发展,超精密运动控制技术越来越受到重视。光刻机是一种光机电一体化的超精密制造设备,其中控制系统决定了光刻机的总体性能。在超精密光刻领域,谐振会影响精密运动系统的稳定性。光刻机系统要求的带宽很高,而机械谐振频率又比较低,导致系统固有机械谐振频率比系统的带宽小,噪声极易引起系统整机谐振,使系统变得不稳定[1]。
基于上述问题,本文采用基于递阶辨识原理的谐振模型辨识策略,对精密运动平台的机械谐振模型进行了参数辨识,建立了一个能够反映系统高频谐振特性的数学模型,并基于谐振模型设计了陷波器。试验结果表明,该方法有效抑制了微动台和宏动台的机械谐振。
1 光刻机平台单自由度数学模型
1.1 光刻机双工件台结构
光刻机双工件台是由平衡质量块、宏动台和微动台3部分组成的。由气浮支撑面将它们组合在一起,进行光刻工作[2]。
平衡质量块由4个气足提供支撑力,使其气浮于底座之上,不与双工件台底座接触,这样可以起到减小摩擦和隔振的作用,大大提高光刻机的精度。
宏动台的两端是直线电机的动子,对于宏动台采用双边驱动的策略,其执行机构是永磁直线电机(permanent magnet linear motor,PMLM)。
微动台的执行机构是音圈电机(voice coil motor,VCM)。整个微动台的底部有气足,同样可以起到减小摩擦和隔振的作用,保证了微动台的稳定性。微动台的顶部是一个具有6个自由度的平台,其上放置硅片,安装有定位装置,可以用双频响激光干涉仪来检查微动台的位置[3]。
1.2 直线电机和音圈电机数学模型
宏动台由永磁直线电机驱动,永磁直线电机的模型在转子dq0旋转坐标系中可以表达为:
(1)
式中:ud、uq为电机定子电压;id、iq为电机定子电流;Ld、Lq为电枢电感,在电枢中相等;λd、λq为磁链;Rs为电枢电阻;Ifd为励磁电流;Lmd为q轴的互感系数;p为极对数。
电磁推力方程为:
f=K[LmdIfdiq+(Ld-Lq)idiq]
(2)
对于固定安装好的永磁直线电机来说,Lmd和Ifd是一个常数,永磁直线电机通常采用矢量控制方法,id=0,所以d轴的磁链λd是固定的,仅iq提供推力。这样,电磁推力直接正比于iq,iq是受闭环控制的。这时式(2)推力方程为:
f=KLmdIfdiq=Kfiq
(3)
式中:Kf为电机推力系数。
永磁直线电机的输出力fe与q轴电流iq成正比,控制q轴的电流即可控制永磁直线电机输出力。
取反电动势系数Ke=pLmdIfd,i=iq,u=uq,那么推力方程为f=Kfi,则可以得到如下所示的电压方程:
(4)
根据牛顿第二定律,忽略电机扰动力等阻力,永磁直线电机带负载运动方程为:
f=ma
(5)
式中:f为永磁直线电机输出的力;a为直线电机加速度。
这样可以提供的模型如下:
(6)
结合式(6),可以得到直线电机的传递函数框图如图1所示。为了区分音圈电机和直线电机,各参数添加下标v表示音圈电机相关参数,添加下标l表示直线电机相关参数。音圈电机模型如图2所示。

图1 直线电机模型

图2 音圈电机模型
由于电气时间常数远小于机械时间常数,电气瞬态响应延迟可以被忽略,那么新的直线电机模型如下:
(7)
同理,建立音圈电机模型:
(8)
1.3 单自由度宏微耦合运动模型
在超精密控制领域,通常采用宏动台来实现高速度长行程运动,采用微动台实现小行程和高精度性能。宏微运动控制结构简化后的模型如图3所示。
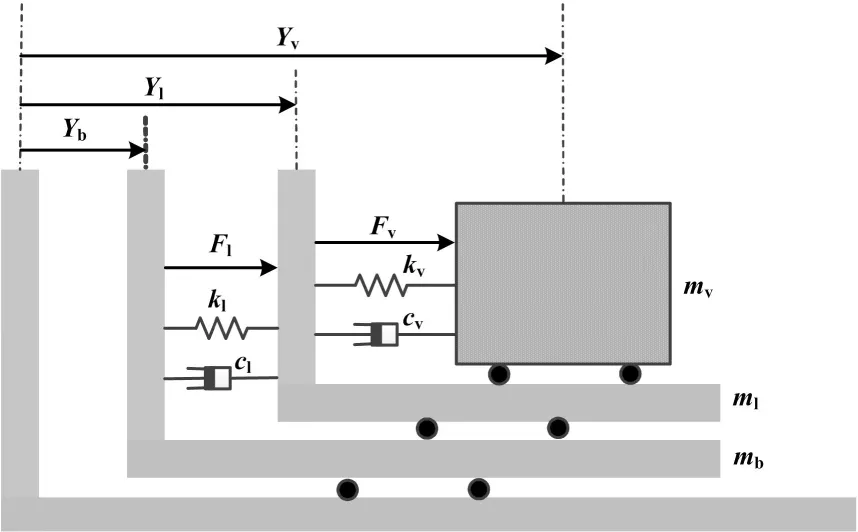
图3 宏微耦合力学模型
微动台、宏动台以及平衡质量块的位移参考位置是相对于地面静止的测量框架。在对硅片台上的晶圆进行扫描过程中,平衡质量块具有和宏动台相反的运动方向,将平衡质量块和宏动台之间视为无外力作用的整体。设初始位置均为零,建立力学方程和位移关系为:
(9)

平台采用气浮导轨支撑,可以忽略其阻尼系数cv、cl和刚度系数kv、kl,那么有:
(10)
精密运动平台y向宏微耦合的模型如图4所示。

图4 宏微耦合等效框图
建立精密运动平台的y向宏微耦合模型可以表示如下:
(11)
即:
(12)
实际中的精密运动平台参数如表1所示。

表1 电机参数参考值
根据表1,计算得到如下数值:Kev=42.218 8,Kel=43.399 4,Rvmv/Kfv=3.087 8,Rlmv/Kfl=0.539 1,Rlml/Kfl=1.290 9。
所以,精密运动平台的y向宏微耦合模型为:
2 机械谐振模型及参数递阶辨识
2.1 机械谐振模型
因为精密运动平台不是理想的刚体,机械谐振不可避免地存在于精密运动系统中,这是机电耦合的结果。如果将系统中的执行元件视为理想的刚体,对电机进行建模的过程中,常常将谐振模态当做系统未建模动态来考虑[4-6]。系统的谐振频率ωm较高,作为未建模动态来处理时,那么系统的带宽应该限制为:
ωBW<ωm/5
(13)
但是,如果系统的带宽要求很高,而机械谐振频率又比较低,那么如果两者很接近,或者系统固有机械谐振频率比系统的带宽小,噪声极易引起系统整机谐振,反馈又会加剧谐振,这样可能会使系统变得不稳定[7]。
被控对象包含机械谐振时,其开环Bode图在穿越0 dB线以后又回升到了0 dB线上,会使系统动态指标偏离理想值,甚至使系统稳定性变差或者不稳定。所以,抑制精密运动平台的机械谐振是十分重要的。
通过扫频试验,可以得到精密运动平台的频率特性数据。由数据可以看出,在低频频率段时跟理想模型是相符的,但是往往在较高频率段的数据已经和理想模型出现了很大的差异。显然,对于一个已经加工好的精密机械系统,改进机械系统结构是一个很费成本和不现实的情况,而精密运动系统又不能忽略谐振的影响,所以一般会先尝试从伺服控制系统设计的角度解决这个问题[8]。
对于精密运动平台的机械谐振来说,可以将其表示为许多个二阶环节串联的模式。由调试经验可知,谐振模型可以表示为二阶环节:
(14)
式中:ωc为系统谐振的中心频率;a、b为大于0的浮点数。
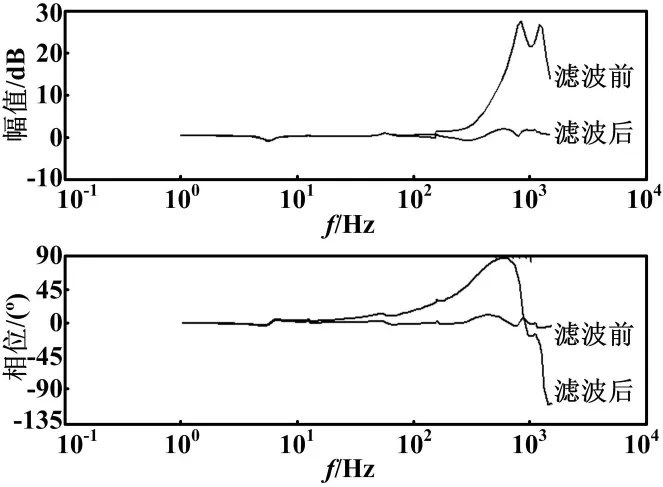
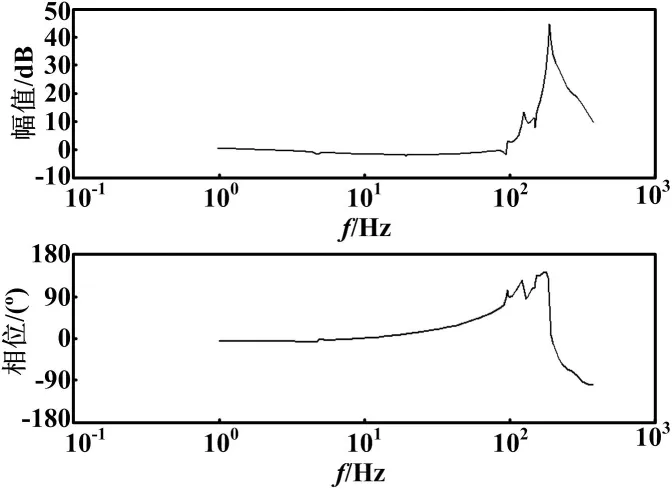
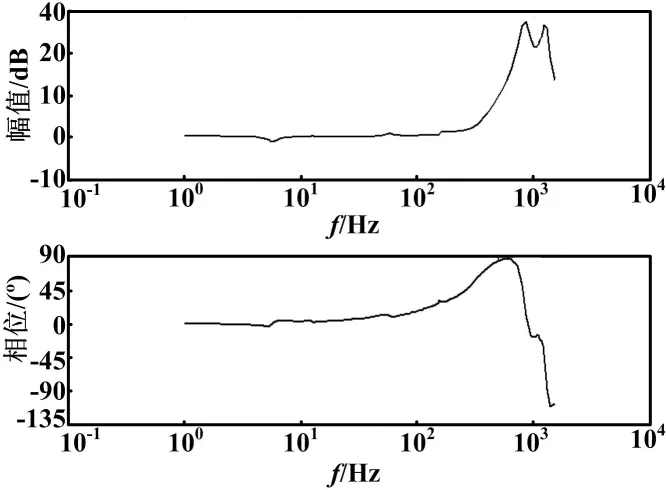
当a>b时,谐振被称为正谐振;a 2.2 参数递阶辨识 在工程中,常用递阶辨识来建立系统的模型。递阶辨识就是将复杂系统分为一个个微小子模型,通过参数优化等方法使模型和真实系统之间的误差变得极小,确定模型的参数。 对于系统的高频域模型辨识,往往采用递阶辨识方法,将模型分为各个子模型: G(jω)=Go(jω)Gr1(jω)Gr2(jω)…Grn(jω) (15) 式中:Go(jω)为低频段理想模型,Gr1(jω),Gr2(jω),Gr3(jω),…,Grn(jω)为高频段机械谐振模型。 然后再对每个高频段机械谐振模型的参数进行分段辨识。具体方法是先从全频率数据中修正掉低频段理想模型,基于修正后的模型与实际平台数据之间的误差来逐次确定其他高频部分的参数。 本章在已知精密运动平台单自由度耦合模型结构的情况下,基于递阶辨识原理,对精密运动平台的机械谐振模型进行了参数辨识,建立了一个能够反映系统高频谐振特性的数学模型,并基于谐振模型设计陷波器,有利于控制系统的设计[10-12]。 3.1 宏动台机械谐振辨识及其抑制方法 3.1.1 宏动台机械谐振辨识 通过扫频试验、数据插值和滤波、相关分析算法计算幅值比和相角差,最终得到宏动台的开环频率特性G(jω)。从系统开环频率特性中剔除掉已知的低频理论模型的频率特性: (16) 剩下的频率特性为各谐振的频率响应: (17) 宏动台机械谐振频率特性如图5所示。 图5 宏动台机械谐振频率特性 由图5可以看出,机械谐振模型: (18) 其幅值特性和相频特性分别为: 可知系统第一个谐振频率在90 Hz和100 Hz之间,且是负谐振,a (19) 辨识结果为: (20) 修正第一个谐振模型后的频率特性如图6所示。 图6 修正第一个谐振模型后的频率特性 再按照同样的方法进行参数辨识,依次得到系统中较为明显的谐振模型: (21) (22) (23) 3.1.2 宏动台机械谐振的抑制方法 本文在辨识出机械谐振模型的基础上,采用加陷波器的方案来抑制谐振。陷波器是一种带宽很窄的带阻滤波器。理想情况下,陷波器只有一个阻带频率点,采用其可以消除系统中该频率点处的分量,其他频率的分量不受影响,故可以用来消除机械谐振,从而拓展系统的带宽。已知系统机械谐振模型为: (24) 那么相对应的,可以设计陷波器抑制机械谐振: (25) 根据其谐振模型,设计相对应的陷波器为 (26) (27) (28) (29) 将陷波器和宏动台串联,则可以得到系统滤波前和滤波后不同的开环频率特性。图7是宏动台的机械谐振特性和添加陷波器后的系统频率特性。从图7可以看出,系统的主要机械谐振得到了有效的抑制,这也证明辨识出的机械谐振模型是可信的。 图7 补偿前后的宏动台频率特性 3.2 微动台机械谐振辨识及其抑制方法 3.2.1 微动台机械谐振辨识 微动台机械谐波辨识流程也是通过扫频试验、数据插值和滤波、相关分析算法计算幅值比和相角差,最终得到精密运动平台微动台的开环频率特性G(jω)。从系统开环频率特性中剔除掉已知的低频理论模型的频率特性,如图8所示,该频率特性即可以认为是微动台的机械谐振特性。和宏动台的机械谐振辨识一样,基于递阶辨识原理对谐振模型分段辨识[13]。 图8 微动台的机械谐振特性 辨识出的两个主要机械谐振模型为: (30) (31) 3.2.2 微动台机械谐振的抑制方法 采用和宏动台相同的方法来抑制微动台的机械谐振,根据已经辨识出的微动台的机械谐振模型,设计陷波器为: (32) (33) 按照示意将陷波器和微动台模型串联,则可以得到系统滤波前和滤波后不同的开环频率特性。图9是微动台的机械谐振特性和添加陷波器后的系统频率特性。从图9可以看出,微动台的主要机械谐振得到了有效的补偿。这也证明了机械谐振模型的有效性,模型是可信的。 图9 补偿前后的微动台频率特性 本文首先研究了精密运动平台的机械结构和工作原理,建立了其单自由度宏微耦合模型,得到了微动台位移、宏动台位移与直线电机、音圈电机输入电压之间的关系。由于理论建模中未考虑机械谐振,而机械谐振对光刻系统的带宽影响是显著的,所以本文建立了机械谐振模型。然后基于递阶辨识原理对谐振模型分段辨识,得到的就是机械谐振的频率特性。基于辨识出的机械谐振模型,设计了相应的陷波器,有效抑制了微动台和宏动台的机械谐振。 [1] Yang C,Zhang Z,Zhao Q.The study on precision positioning system of two-dimensional platform based on high speed and large range[J].Precision Engineering,2010,34(3):640-646. [2] Yang S M,Wang S C.Detection of resonance frequency in motion control systems[C]//Energy Conversion Congress and Exposition(ECCE),2013 IEEE,2013:3757-3761. [3] 曾鸣,张东纯,苏宝库.伺服转台高精度控制系统带宽设计的探讨[J].中国惯性技术学报,2001(2):56-60. [4] 张尚盈,陈学东,赵慧,等.超精密工件台的运动控制[J].华中科技大学学报:自然科学版,2008(10):009. [5] 赵霞,姚郁.递阶辨识方法在转台伺服系统调试中的应用研究[J].控制理论与应用,2002,19(2):229-234. [6] 董立立,赵益萍,梁林泉,等.机械优化设计理论方法研究综述[J].机床与液压,2010(15):114-119. [7] Wang D,Ding R,Dong X.Iterative parameter estimation for a class of multivariable systems based on the hierarchical identification principle and the gradient search[J].Circuits, Systems, and Signal Processing,2012,31(6):2167-2177. [8] 杨一博,尹文生,汪劲松,等.粗精动运动平台的系统辨识激励信号优化设计[J].机械工程学报,2010(9):165-170. [9] 王帅,陈涛,李洪文,等.光电跟踪伺服系统的频率特性测试与模型辨识[J].光学精密工程,2009(1):78-84. [10]Lei J,Luo X,Chen X,et al.Modeling and analysis of a 3-DOF Lorentz-force-driven planar motion stage for nanopositioning[J].Mechatronics,2010,20(5):553-565. [11]Slocum A,Basaran M,Cortesi R,et al.Linear motion carriage with aerostatic bearings preloaded by inclined iron core linear electric motor[J].Precision Engineering,2003,27(4):382-394. [12]Wang D,Ding R,Dong X.Iterative parameter estimation for a class of multivariable systems based on the hierarchical identification principle and the gradient search[J].Circuits,Systems,and Signal Processing,2012,31(6):2167-2177. [13]Ha J L,Fung R F,Han C F.Optimization of an impact drive mechanism based on real-coded genetic algorithm[J].Sensors and Actuators A:Physical,2005,121(2):488-493. Model Recognition of Lithography Motion Stage System In view of the influence of the mechanical resonance on ultra-precision lithography system, the macro-micro motion stage containing mechanical resonance is recognized for suppressing the mechanical resonance. Firstly, the single degree of freedom(SDOF) macro-micro coupling model and resonance model are built, then, based on hierarchical recognition principle, the mechanical model is recognized segmentally, finally, the notch filter is designed based on resonance model for suppressing the mechanical resonance. The test results show that this method effectively suppresses the mechanical resonance of the macro-micro stage, and greatly improves the dynamic response of the system. Lithography Macro-micro coupling model Mechanical resonance Hierarchical recognition Dynamic response 国家科技重大专项基金资助项目(编号:2009ZX02207)。 范文超(1990-),男,现为哈尔滨工业大学控制科学与工程专业在读硕士研究生;主要从事嵌入式系统设计和运动控制的研究。 TP273 A 10.16086/j.cnki.issn1000-0380.201505002 修改稿收到日期:2014-08-25。3 精密运动平台模型辨识及有效性验证试验


4 结束语
