带扰动离散非线性系统的小波自适应滑模控制

张晓宇 陈文卓

(华北科技学院电子信息工程学院，北京 101601)

带扰动离散非线性系统的小波自适应滑模控制

张晓宇 陈文卓

(华北科技学院电子信息工程学院，北京 101601)

在实际控制系统中，非线性、未建模动态和外扰经常是不可估计或无法测量的。采用小波网络(WN)设计动态未知的离散非线性系统智能自适应滑模控制(ASMC)，应用WN构造滑模控制律的等价控制，使用合适的自适应律在线调节网络参数。系统的滑模能够保证在有限时间到达切换带，所得到的闭环系统是渐近稳定的。通过扰动分析表明，所设计的控制器具有较强的鲁棒性。基于倒立摆试验系统的仿真及应用研究证明了其可行性和有效性。

离散非线性系统 多变量系统 小波网络 滑模控制 自适应

0 引言

滑模控制是非线性系统常用的综合方法之一[1-2]。然而，当系统非线性动态未知时，滑模控制设计就非常困难。此时，基于小波网络等价控制逼近就成为较好的辨识工具之一[3-5]。然而许多小波网络的应用研究都是离线辨识或训练[6-8]。对于控制系统来说，需要能够实现在线辨识和逼近，或获得在线自适应逼近器[9-12]，小波网络(wavelet network,WN)完全能够胜任。许多学者基于小波网络进行自适应滑模控制研究[13-26],如Wai R J 针对电机控制问题的研究[13-15],Xu J X 对非线性系统的自适应滑模控制研究[16-17]，王家军结合反推方法的感应电机控制研究[18],李毓洲、潘劲等针对电机控制的研究[19-20]以及其他诸多研究[21-25]。然而这些工作都是针对连续系统，且都没有考虑非仿射非线性系统。

本文考虑将自适应小波网络及滑模控制推广至一类带外部扰动的离散非仿射非线性系统。这样代表更广泛的实际工业过程或被控对象，便于计算机实现。当对象模型动态未知时，利用小波网络逼近等价控制，实现滑模控制综合,削弱滑模控制抖振，同时滑模控制对匹配不确定性和干扰的鲁棒性仍然得以保存。

1 问题描述

考虑如下一类离散多变量非仿射非线性系统：

(1)

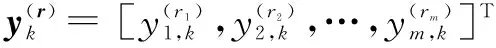
非线性动态f(xk,uk)=[f1(xk,u1,k),f2(xk,u1,k),…,fm(xk,u1,k)]构成系统动态函数向量。这里fi(xk,ui,k)∈L2(R),i=1,2,…,m都是未知的。d(xk,k)=[d1(xk,k),d2(xk,k),… ,dm(xk,k)]T是系统未知的有界干扰，这里di(xk,k)∈R, 干扰上界描述为：

|di(xk,k)|≤DiDi≥0i=1,2,…,m

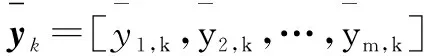
(2)

渐近收敛到原点，这里：

定义滑模面如下：

Sk=[S1,k,S2,k,…,Sm,k]T

(3)

式中：Si,k=Ciei,i=1,2,…,m，Ci=[ci,1,ci,2,…, ci,ri-1,1]T满足Hurwitz多项式。

hi(ei,k)=ei,k+ri-1+ci,ri-1ei,k+ri-2+…+ci,1ei,k

(4)

控制问题是寻找SMC控制：

ui,k=ueq,i+uv,ii=1,2,…,m

(5)

这里ueq,i是等价控制， uv,i是保证滑模面Sk可以到达并保持的到达控制率。到达条件可以选择为Lyapunov型：

(6)

式中：ΔSi,k=Si,k+1-Si,k为子滑模Si,k的前向差分。式(6)也可以写成求和式：

(7)

到达条件(6)将会使滑模面渐近收敛到原点。因为非线性动态 fi(xk,ui,k) 是未知的，控制输入uk不能直接设计。接下来，将采用一个自适应小波网络来实现这个SMC控制器。

后面的设计中，将基于如下假设。

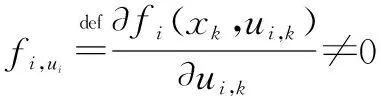
对于所有xk∈Ωxk光滑函数满足fi,ui>0或fi,ui<0。不失一般性，假设fi,ui>0。

假设2 存在正标量ζi,1、ζi,2及 ζi,3使得∀x∈Ωx、ζi,1≤fi,ui≤ζi,2和Δfi,ui≤ζi,3成立。

根据隐函数定理，下列引理被引入。

引理2 对于式(1)，存在一个子集Ωx,0∈Ωxk及独立局部解ui,k=ui(xk,vi)，使得fi(xk,ui,k)+ vi=0对于∀x(0)∈Ωx,0，i=1,2,…,m都成立。其中vi=vi(x)是xk的任意光滑函数。

2 小波网络

小波网络是建立在多分辨分析(multi-resolutionanalysis,MRA)基础之上的一种函数逼近方法。许多关于MRA的理论可以参考文献[3]～[5]和文献[8]。

这里ef,j是分辨率j的估计误差。随着j→,lim|ef,j|=0。在分辨率(j+1)， f(x)的逼近在空间Wj上有投影，被称为“细节”。

显然，|ef,j|>|ef,j+1|>…，随着j→，越来越多的细节被加入到f(x)估计中去。因此对于给定J，f(x) 在空间VJ上的投影被称作“粗糙”估计。随着分辨率j的增加，细节估计累积起来。自然地，存在一个“母小波”k∈Z，可以构成空间Wj的规范基。与尺度函数类似，小波函数ψj,k也满足：

则L2(R)中，∀f(x)自然可以写成：

(8)

式(8)是L2(R)空间上函数f(x)基于尺度基序列和小波基序列的估计。在实际应用中，函数估计是在有限维空间进行的，因此式(8)只存在理论上的意义，是不能应用的。由文献[8]引入如下定理。

(9)

这就意味着总存在一个以小波基序列形式的函数最优估计：

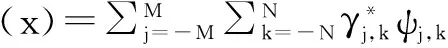
由此，当J≤-M时，估计：

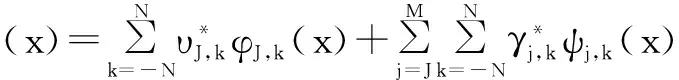
实际应用中还有一个问题是，控制系统往往是多维的。系统状态变量x是一个向量而不是单变量。尺度函数基及小波基必须扩展为如下多维形式：

这样f(x)估计变为：

(10)

这里：

Υ=[υJ,-N,υJ,-N+1,…,υN]T

(11)

Γj=[γj,-N,γj,-N+1,…,γj,N]T

(12)

ΦJ=[φJ,-N(x),φJ,-N+1(x),…,φJ,N(x)]T

(13)

Ψj=[ψj,-N(x),ψj,-N+1(x),…,ψj,N(x)]T

(14)

上述表明，L2(R)空间上任意函数f(x)都有一个基于尺度基和小波基的最优估计f*(x)。

3 基于自适应WN的SMC

现在寻找滑模(2)、(3)的子滑模Si,k(由于对称性，在下文中我们只考虑子滑模Si,k)的差分：

如果定义：

那么：

ΔSi,k=vi+fi(xk,ui,k)+di(xk,k)

(15)

控制目标是设计一个滑模控制ui,k使 Si,k=0。由式(5)描述的滑模控制由两部分组成：等价控制ueq,i和到达控制uv,i。因为系统的非线性动态都是未知的，采用上节描述的基于小波网络的函数逼近方法来估计等价控制。我们首先来设计等价控制ueq,i的估计。

3.1 等价控制设计

系统动态函数 fi(xk,ui,k) 满足假设1和2。根据引理1，当外部干扰 di(xk,k)不被考虑时，存在等价控制 ueq,i(xk,vi) 使 Si,k=0，即式(15)变为:

ΔSi,k=vi+fi(xk,ueq,i)=0

(16)

因fi(xk,ui,k)∈L2(R)，等价控制 ueq,i(xk,vi) 也位于L2(R)内。

根据定理1及式(10)，存在 ueq,i(xk,vi) 的最优估计如下:

Ψj(xk,vi)=[ψj,-N(xk,vi),…,ψj,N(xk,vi)]T

ΦJ(xk,vi)=[φJ,-N(xk,vi),…,φJ,N(xk,vi)]T

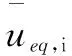
(17)

这里Υi及Γi,j为小波基系数，需要用自适应率:

(18)

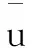
然而，即使是最优逼近在实际系统中也存在着一些误差：

这样再考虑式(16)，则有：

(19)

由上式可见，估计误差使Si,k趋向ΔSi,k≠0，必须有到达控制 uv,i才使到达条件(6)得到满足。

3.2 到达控制设计

单凭等价控制不能保证滑模面的到达，这在滑模控制的一般原理中也是如此。单纯的等价控制就不能构成滑模控制系统，也失去了其鲁棒性能。因此到达控制项是必需的。依据滑模控制的基本理论[1-2]，我们可以设计到达控制项uv,i为：

uv,i=-kiSi,k-ηisgn[Si,k]

(20)

这里参数ki和ηi分别满足：

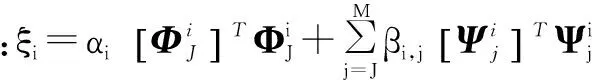
(21)

相应地，滑模Si,k的前向差分(19)可以写为：

(22)

3.3 稳定性分析

主要结果概括为如下定理2。

定理2 基于假设1～3，系统(1)在小波自适应滑模控制(AWSMC)(17)、(20)、(22)及自适应律(18)作用下,滑模Si,k能够到达如下切换带：

(23)

这里：

(24)

证明 选择Si,k的Lyapunov函数为：

将自适应律(18)代入上式，有

(25)

接着考虑以下两种情况。

① 如果Si,k>φi，则根据式(24)和假设3，下式成立：

那么有：

即：

因此ΔVi,k≤0。

② 如果Si,k<-φi，则根据式(24)和假设3，下式成立：

那么同样有:

即：

因此ΔVi,k≤0。

3.4 外扰分析

现在考虑外扰di(xk,k)，将其写为：

di(xk,k)=di,um(xk,k)+fi,ukdi,ma(xk,k)

式中：di,um(xk,k)为不匹配干扰；di,ma(xk,k)为匹配干扰。二者都上界，分别是：

有界干扰代入式(15)、式(16)，然后式(19)变为：

为了补偿匹配干扰，只需要在到达控制(20)中，使：

(26)

后续并不影响定理2的证明。这充分表明了滑模控制对匹配干扰的完全补偿特性。

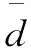
(27)

则定理2证明过程仍然有效。

滑模控制有一个重要的问题是抖振。这个问题已经被许多学者所研究[27-29]， 这其中的许多结果都可以被应用。例如，可采用文献[27]的到达控制项：

uv,i=-kiSi-ηisat(Si)

(28)

这里sat(x)是饱和函数。

(29)

式中：Δ>0是可选的正标量，即边界层厚度。

4 应用仿真

考虑一阶倒立摆的控制问题，设其精确非线性动态是未知的。本文提出的AWSMC控制设计不需要系统精确数学模型,因而只考虑其粗略离散模型。

x1,k+1=x2,k,x2,k+1=f(xk,uk)

这里xk=[x1,k,x2,k]T=[θk,θk+1]T为系统状态，uk为小车电机的控制电压，θk为摆角位移。

然后，估计其未知动态边界为：

20≤fui,k≤30，Δfui,k≤200

滑模选为Sk=[c,1]xk，其中c>0。选取最简单的Haar小波，即：

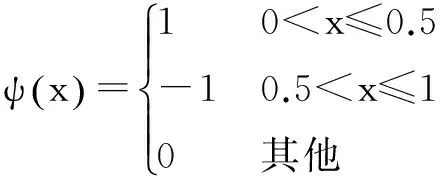
(30)

相应的尺度基函数为：

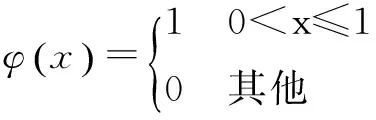
(31)

首先我们基于原点线性化，做了一般SMC控制试验，极点配置在-10.91±7.22i处，得到摆角位移曲线如图1虚线所示，相应小车控制电压曲线如图2虚线所示。

图1 摆角位移曲线图

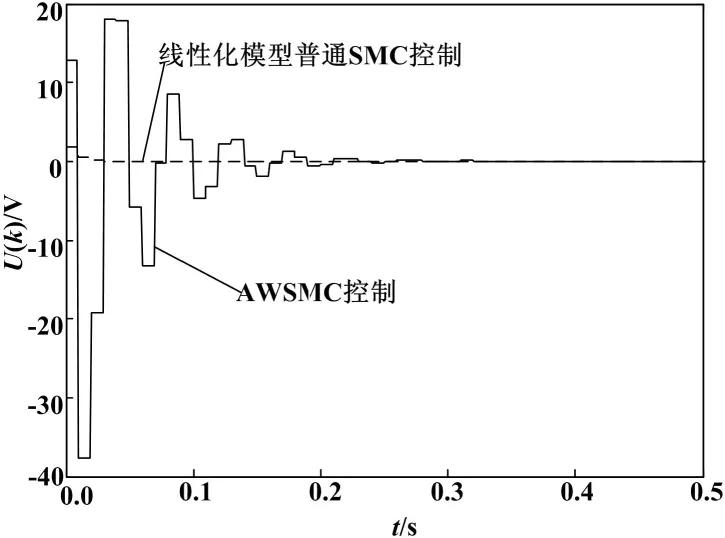
图2 控制电压曲线图

接着我们验证AWSMC 的抗外扰能力。用幅值0.3 rad、宽度0.2 s的脉冲外扰施加到摆角。为抵抗外扰，把控制器到达控制项参数η改为0.5，AWSMC仍然能够使系统稳定，摆角位移如图3所示，相应控制电压如图4所示。抗扰性能得到了验证。

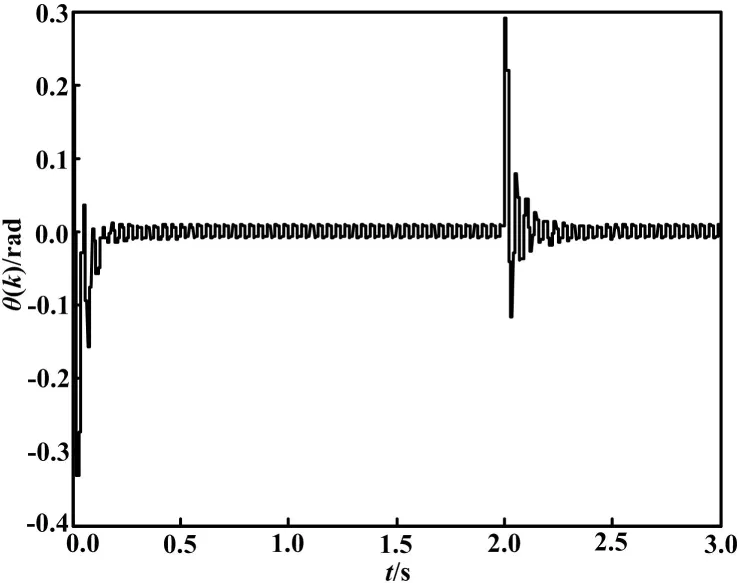
图3 AWSMC控制受扰下摆角位移曲线

图4 AWSMC控制受扰下控制电压曲线

5 结束语

对于一类MIMO带扰动的离散非仿射非线性系统，提出了基于小波网络的自适应滑模控制设计。在系统非线性动态函数未知的情况下，系统的等价控制律用小波网络进行逼近，通过合适的小波网络权参数自适应律保证逼近效果，增加到达控制项保证滑模切换带到达。通过Lyapunov 方法证明了滑模能够渐近到达一个切换带，切换带宽度取决于系统不确定性、外扰的大小。基于倒立摆的仿真研究证明了所提出方法的有效性。

[1] Edwards C，Spurgeon S K.Sliding mode control:theory and applications[M].London,UK:Taylor & Francis,1998.

[2] Slotine J J E，Li W.Applied nonlinear control[M].New Jersey:Prentice-Hall,1991.

[3] Zhang Q,Benvensite A. Wavelet network[J].IEEE Transactions on Neural Networks,1992,3(6):889-898.

[4] Zhang J.Wavelet neural networks for function learning[J].IEEE Transactions on Signal Processing,1995,43(6):1485-1495.

[5] Pati Y C,Krishnaprasad P S.Analysis and synthesis of feedforward neural networks using discrete affine wavelet transformations[J].IEEE Transactions on Neural Network,1993,4(1):73-85.

[6] Zhang Q.Using wavelet network in nonparametric estimation[J].IEEE Transactions on Neural Network,1997,8(2):227-236.

[7] Sureshbabu N,Farrell J A.Wavelet-based system identification for nonlinear control[J]. IEEE Transactions on Automation Conrtol,1999,44(2):412-417.

[8] Delyon B,Juditsky A,Benveniste A.Accuracy analysis for wavelet approximations[J].IEEE Transactions on Neural Network,1995,6(2):332-348.

[9] Sanner R M,Slotine J J E.Gaussian network for direct adaptive control[J].IEEE Transactions on Neural Network,1992,3(6):837-863.

[10]Polycarpou M M,Mears M J.Stable adaptive tracking of uncertain systems using nonlinearly parameterized on-line approximators[J].International Journal of Control,1998,64(2):363-384.

[11]Farrell J A.On performance evaluation in on-line approximation for control[J].IEEE Transactions on Neural Network,1998,9(5):1001-1007.

[12]Sanner R M,Slotine J J E.Structurally dynamic wavelet networks for adaptive control of robotic systems[J].International Journal of Control,1998,70(3):405-421.

[13]Wai R J.Robust control for nonlinear motor mechanism coupling system using wavelet neural network[J].IEEE Transactions on Systems Man and Cyber.Part:B,2003,33(3):489-497.

[14]Wai R J.Wavelet neural network control for induction motor drive using sliding mode technique[J].IEEE Transactions on Industrial Electronics,2003,50(4):733-748.

[15]Wai R J,Chang J M.Implemetation of robust wavelet neural network sliding mode control for inductive servo motor drive[J].IEEE Transactions on Industr.Electr.,2003,50(6):1317-1334.

[16]Xu J X,Tan Y.Nonlinear adaptive wavelet control using constructive wavelet networks[J].IEEE Transactions on Neural Networks,2007,18(1):115-127.

[17]Xu J X,Tan Y.Nonlinear adaptive wavelet control using constructive wavelet networks[C]//Proceedings of the American Control Conference.Arlington,VA:IEEE Press,2001:624-629.

[18]王家军.基于自回归小波神经网络的感应电动机滑模反推控制[J].自动化学报,2009,35(1):1-8.

[19]李毓洲,阳林.基于小波神经网络的永磁同步电机无速度传感器滑模控制[J].电机与控制应用,2010,37(3):31-34.

[20]潘劲,焦晓雷,危韧勇.无位置传感器无刷直流电机全局滑模控制研究[J].机电工程技术,2012,41(9):23-26+96.

[21]周芳,朱齐丹,姜迈,等.受限机械臂的自适应小波滑模位置/力混合控制[J].华中科技大学学报：自然科学版,2009,37(11):9-12.

[22]徐传忠,王永初,杨冠鲁.一种小波提升算法的多关节机器人滑模控制[J].扬州大学学报：自然科学版,2010,13(3):61-64.

[23]王志,吴红芳.基于小波神经网络补偿的飞艇滑模控制[J].西安工业大学学报,2011,31(5):465-469.

[24]胡庆雷,肖冰,马广富.输入受限的航天器姿态调节小波滑模反步控制[J].哈尔滨工业大学学报,2010,42(5):678-682.

[25]Zhang Xizheng，Wang Yaonan.Wavelet neural network based robust sliding-mode control for induction motor[J].Journal of Information & Computational Science,2011,8(7):1209-1216.

[26]Mallat S.Multiresolution approximation and wavelet orthonormal base of L2[J].IEEE Transactions AMS,1989,31(5):69-87.

[27]Slotine J J E,Sastry S S.Tracking control of nonlinear system using sliding surfaces with application to robot manipulators[J].International Journal of Control,1983,38(2):465-492.

[28]Chang F J,Twu S H and Chang S.Adaptive chattering alleviation of variable structure systems control[J].IEE Proceeding-D Control Theory and Applications,1990,137(1):31-38.

[29]Bartolini G.On multi-input chattering-free econd-order sliding mode control[J].IEEE Transactions on Automatic Control,2000,45(9):1711-1717.

Wavelet Adaptive Sliding Mode Control for Discrete Nonlinear Systems with Disturbances

In practical control systems, unusually, the non-linearity, the unmodeled dynamics, and external disturbances are immeasurable and cannot be estimated. Thus the intelligent adaptive sliding mode control (ASMC) based on wavelet network (WN) has been designed for dynamic unknown discrete nonlinear system. The equivalent control of SMC is constructed by WN, the network parameters are tuned online by appropriate adaptive laws. The sliding mode of the system can reach the switching zone in limited time; the closed loop system obtained is asymptotically stable. The disturbance analysis indicates that the controller designed still possesses stronger robustness. The simulation based on experimental system of the inverted pendulum and application research verify its feasibility and effectiveness.

Discrete nonlinear system Multiple variable system Wavelet network Sliding mode control Adaptive

国家自然科学基金青年科学基金资助项目(编号：61304024)；

河北省自然科学基金青年科学基金资助项目(编号：F2013508110)；

中央高校基本科研业务费基金资助项目(编号：3142013055)；

河北省教育厅科技计划基金资助项目(编号：Z2012089)。

张晓宇(1978-)，男，2006年毕业于浙江大学控制科学与工程专业，获博士学位，副教授；主要从事非线性控制、智能控制、复杂系统控制与应用的研究。

TP273

A

10.16086/j.cnki.issn1000-0380.201505001

修改稿收到日期：2014-09-23。