一类非线性军备竞赛博弈的动力学研究

张志攀，阳平华

（1.军械工程学院，石家庄 050003；2.广西崇左军分区，广西 崇左 532200）

一类非线性军备竞赛博弈的动力学研究

张志攀1，2，阳平华1

（1.军械工程学院，石家庄 050003；2.广西崇左军分区，广西 崇左 532200）

针对多国军备竞赛问题，基于混沌动力学理论，并考虑到非线性因素对军备竞赛的影响，改进了理查森军备竞赛模型，建立了三国非线性军备竞赛的动力学模型，通过Matlab数值仿真表明，各博弈方的预期函数影响军备竞赛的稳定性，通过调整国家的不同预期函数变量，能够使军备竞赛从混沌逐步趋于稳定，这一结果将为国际军控研究提供一定的参考。

军备竞赛，理查森模型，混沌，动力学

0 引言

当今世界并不太平，国家间的军备竞赛随处可见，在中东，以色列、伊朗、沙特都有称霸中东的企图，力图通过大量采购军火来确保自己的军事优势；在南亚，巴基斯坦与印度处于全天候地对抗状态，在核试验、常规武器采购等方面你追我赶；在东亚，朝鲜执意发展自己的核力量，与美、日、韩三国针锋相对，毫不退让。虽然国际社会对控制军备竞赛作出各种努力，但是收效却不是十分明显。军备竞赛的研究兴起于冷战时期，由于对美苏两个超级大国军备竞赛的担忧，学者们试图从理论角度证明军备竞赛的可控性。在军备竞赛的博弈中，国家是理性的局中人，为了使自身的利益最大化，它必须通过观察对手的情况并结合自身实际，做出自己的策略选择。早期军备竞赛模型的研究对象为两个国家，通过建立微分方程来反应国家军备竞赛中策略的相互影响关系，如理查森模型。但是，现实世界中军备竞赛往往不止限于两个国家，而是在多个国家之间发生。

近来年，一些学者对经典军备竞赛模型进行了改进，并围绕军备竞赛的稳定性问题展开了讨论，形成了3种不同的观点［1］：①认为军备竞赛存在稳定性，代表人物为Richardson；②认为军备数量呈非线性增长，最终将导致军备竞赛失稳，代表人物为MacGuire；③认为军备竞赛的稳定性仅限于局部地区，代表人物为Brito。同时国内许多学者也致力于军备竞赛稳定性的研究，骆桦［2］对超级大国主导下的军备竞赛稳定性进行研究，得到了单极世界军备竞赛的稳定条件。刘光华［3］结合有限理性的博弈特点，建立了两国军备竞赛的动力系统模型。本文在相关文献研究的基础上，通过改进经典模型中的影响因子，建立了非线性的三国军备竞赛博弈模型。

1 理查森军备竞赛模型介绍

理查森军备竞赛模型［4］是研究军备竞赛的主要模型之一，它是一种描述性的模型，即没有目标函数，也没有最大化假设，通过建立微分方程，描述在两个国家间武器变化的模型。设A、B两国军备是同质的，其数量分别用x（t）、y（t）表示，国家的军备增长比率与3个因素有关：①敌对国家的军备情况对本国军备增长的刺激作用；②本国已有的军备情况对本国军备增长的抑制作用；③由敌我双方情况演变而成的其他复杂因素也会影响本国军备数量，则两国军备竞赛的微分方程组可表示为：

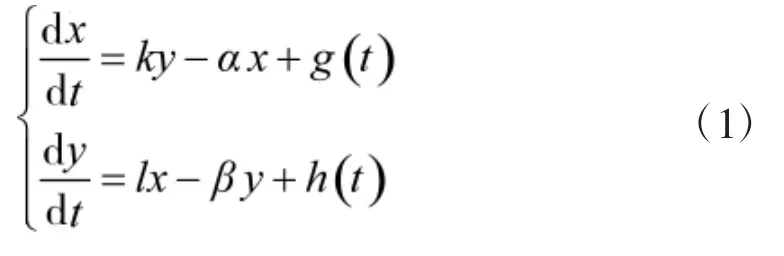
其中，k，α，l，β＞0，且为常数。当两国军备数量不再变化，可得到反应方程，即本国的军备数量为另一国的函数：

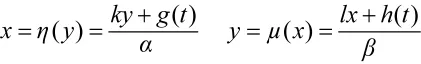
当kl-αβ＞0，g（t）≡g，h（t）≡h时，均衡解为：

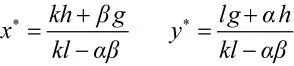
2 改进的理查森军备竞赛模型研究

理查森军备竞赛模型研究对象是两个国家，且国家间的相互关系是线性的，但现实中军备竞赛常常在多个国家出现，并且他们之间存在非线性的关系，军备并不是简单地军备数量上的竞争，更是军备质量、科研水平、持续发展潜力上的竞争，理查森军备竞赛模型仅仅建立的线性竞争模型显得过于简单。各国之所以能够进行军备竞赛，源于国家经济的迅速增长，军备增长与经济增长存在明显的趋同关系［5-6］。为此，对理查森军备竞赛模型进行了改进来研究多国非线性军备竞赛的问题。以三国军备竞赛为例，假设A、B、C三国军备数量分别用x（t）、y（t）、z（t）表示，且三国之间是独立的理性个体，不与任何国家结盟，由于不同信念国家军备竞赛的模型不同，关系较为复杂，这里仅研究信念相同国家的军备竞赛情况，即A、B、C三国在考虑军备竞赛时其模型是相似的。我们认为，军备竞赛依然是受三个方面的制约：对方实力，我方实力，其他复杂因素。考虑军备质量与数量间的倍增关系，设敌国军备数量对本国军备竞赛的促进作用是非线性二次函数关系，敌我双方复杂因素对军备竞赛的影响既与本国军备数量有关，也与敌对国家军备数量相关，也是非线性二次函数关系。二次函数的特点与经济成本增长规律一致［7］，同时又由于经济增长与军备竞赛的趋同关系，所以二次函数模型符合国家间军备增长的规律。因此，三国军备竞赛的微分方程组为：

式中a1，a2，a3分别为对方军备数量对国家的刺激系数，b1，b2，b3分别为本国军备数量对自身军备扩张的抑制系数，（c1，d1，f1），（c2，d2，f2），（c3，d3，f3）分别为其他复杂因数对军备竞赛的混合影响系数，且。由a1，a2，a3，b1，b2，b3，c1，c2，c3，d1，d2，d3，f1，f2，f3＞0二次函数的性质可知，当函数位于对称轴右侧时，函数值是随自变量单调递增的；当函数位于对称轴左侧时，函数值是随自变量单调递减的。x，y，z∈［0，1］，表示三国标准化后的军备数量。

对于方程（2），其反应方程为：

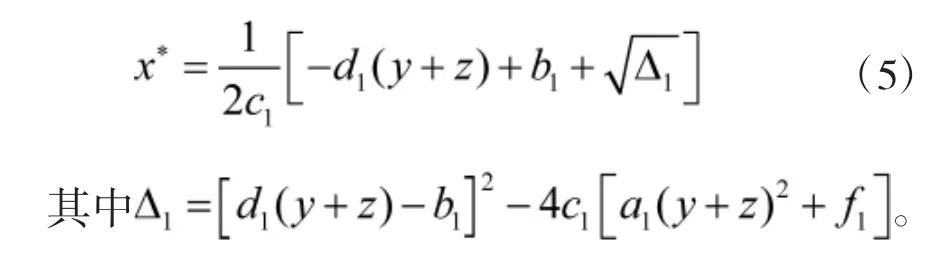
对于方程（3），其反应方程为：

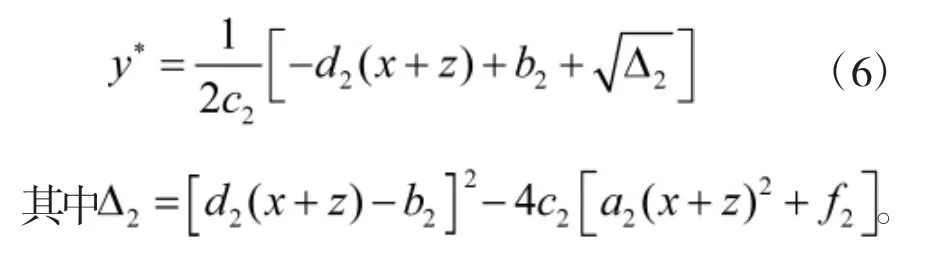
对于方程（4），其反应方程为：

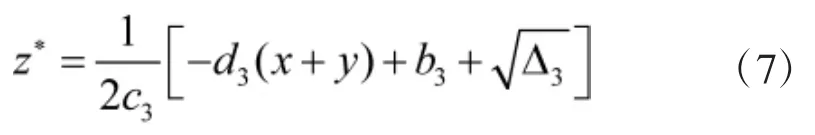
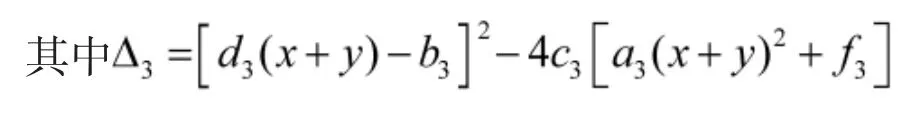
由反应方程可以看出，三国的军备水平是相互依赖的，其某一时期的军备数量与其他两个国家密切相关，一个国家是否增加军备数量，必须充分考虑其他国家的军备水平。国家之间的决策是一个动态的决策过程，其对下一时期的决策会有一个预期。由于国家自身发展水平的不一样，其策略预期函数均不相同。

实力弱小的国家往往只能按部就班确定自己军备数量，其表示为：

实力中等的国家则依据这一时期的自己军备数量与反应方程的差值自动调整下一时期军备数量，若高于反应方程值，则再下一轮军备调整需减少军备的增长数量，反之，则增加军备增长的数量，其表示为：

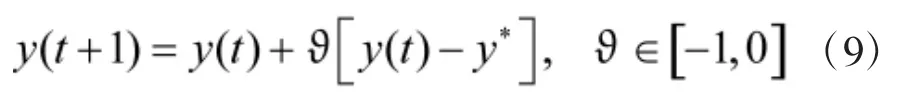
实力较强的国家则依据军备数量增长的速率自动调整下一时期军备数量，如果这一时期军备数量增长率为正，则减少下一时期的军备数量，反之，则增加下一时期的军备数量，其表示为：

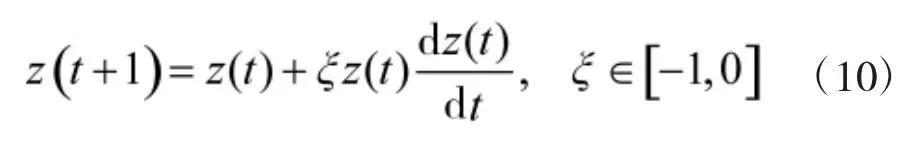
将式（5）代入式（8）得：

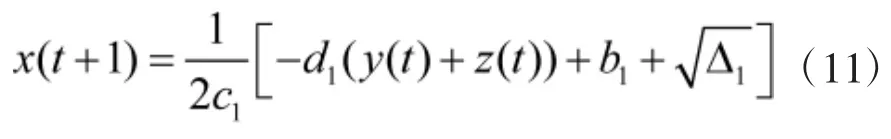
将式（6）代入式（9）得：

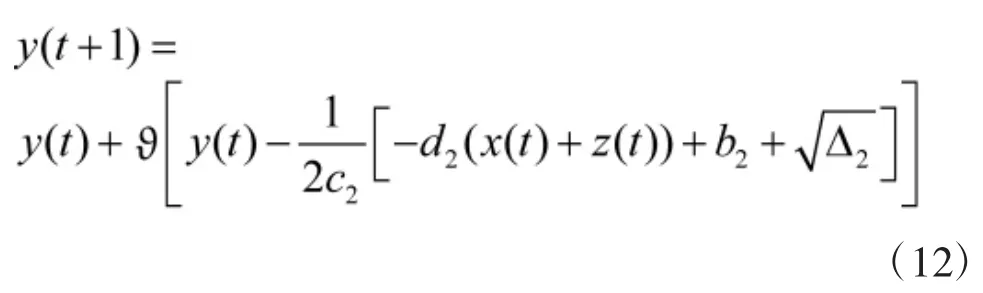
将式（4）代入式（10）得：

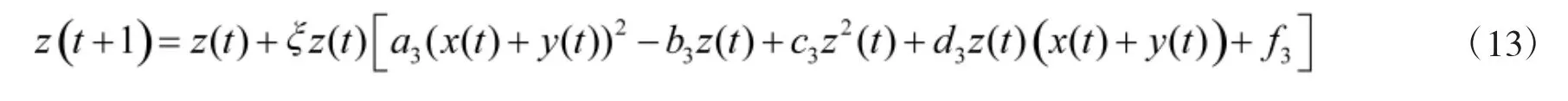
3 军备竞赛模型的动力学研究

如果将3个国家以及它们之间的关系看成一个系统，那么军备竞赛行为随时间发生变化就使得这三国构成了一个动力系统。军备竞赛的动力学行为就是偏离平衡态而发生变化的过程，因此，首先必须要确定动力系统方程组的稳定状态。通过由式（11）～式（13）组成的动力系统方程组求解雅可比矩阵［8］：

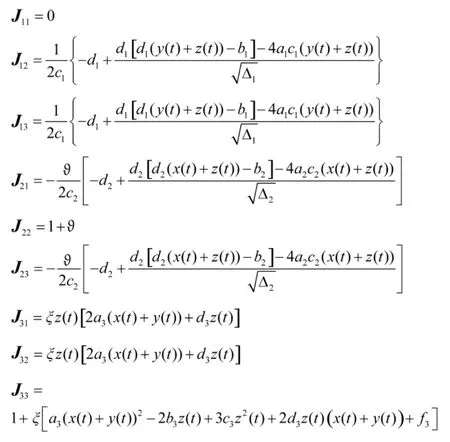
取a1=a2=a3=1，b1=0.08，b2=0.07，b3=0.06，c1=3.02，c2=3.04，c3=3.06，d1=d2=d3，f1=-4，f2=-4.2，f3=4.4。令x（t+1）=x（t），y（t+1）=y（t），z（t+1）=z（t），取弱国x的军备数量初值为0.2，中等国家y的军备数量初值为0.5，强国z的军备数量初值为0.8，且x，y，z均大于零，则纳什均衡点为：

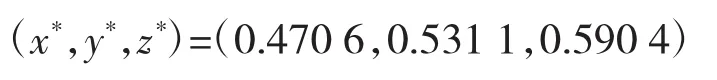
在均衡点处，其雅可比矩阵为：

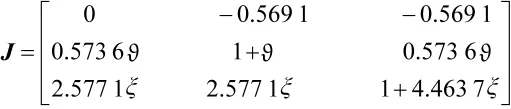
其特征方程为：

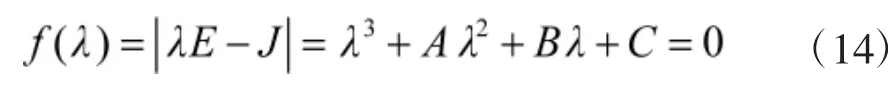
其中：

对于判定差分方程组系统的稳定性，有如下判定定理。

定理1［9］设齐次线性常系数差分方程组为：

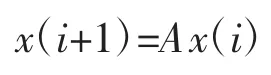
则该系统是渐进稳定的充分必要条件为：A的所有特征值在复平面的单位圆内。

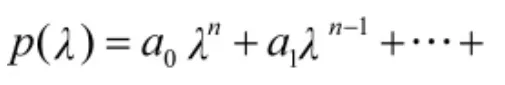
表1 多项式系数关系表

其中

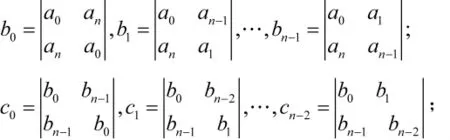
依次类推，直到一行只有3个元素为止，则p（λ）所有零点在复平面单位圆内的充分必要条件是

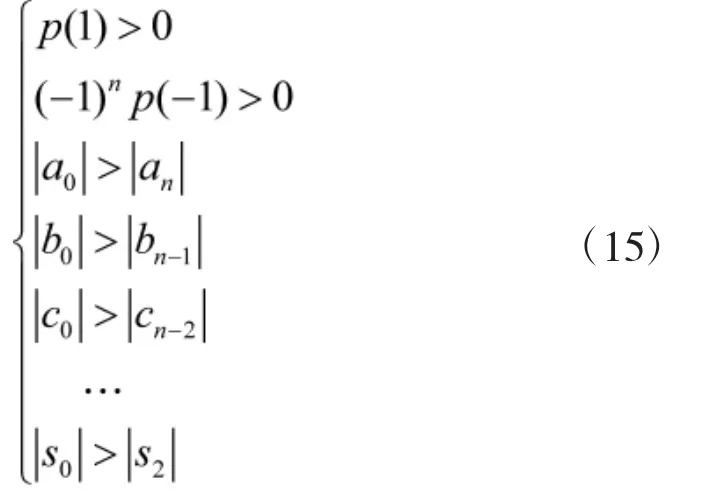
条件（15）即为Routh-Hurwitz判据，当特征方程（14）满足条件（15）时，则由方程（11）～方程（13）组成的差分方程系统在不动点（x*，y*，z*）处是稳定的。其稳定区域如图1所示。

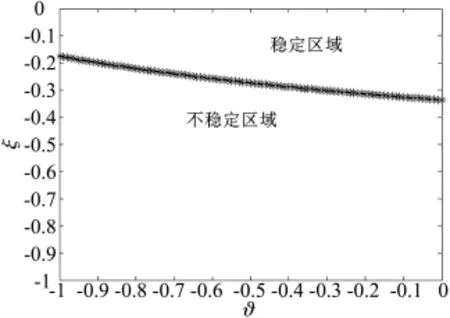
图1 三国军备竞赛在不动点的稳定区域

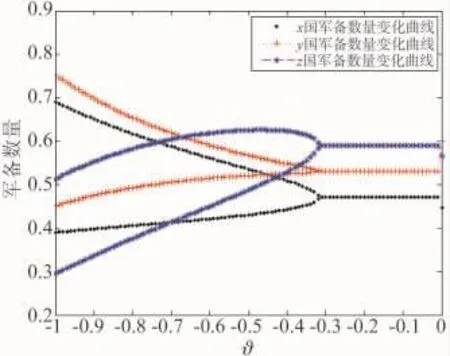
图2 ξ=-0.3时三国军备竞赛随ϑ变化的分叉图

由图1可以看出，当-0.176≤ξ＜0时，无论ϑ取何值，三国博弈处于稳定状态。当-0.337＜ξ＜-0.176，三国军备竞赛的稳定状态与ϑ有关。如图2所示，即表示当ξ=-0.3时，三国军备竞赛随ϑ变化的分叉图。

由图2可以看出，当ξ=-0.3，ϑ＜-0.31时，三国军备竞赛处于二倍周期分叉状态；当ϑ≥-0.31三国军备竞赛稳定在不动点处。

由图3可以看出，当ϑ=-0.1，ξ≥-0.32时，三国军备竞赛稳定在不动点；当ξ＜-0.32时，三国军备竞赛处于不稳定状态，当ξ＜-0.54三国军备竞赛处于混沌状态。

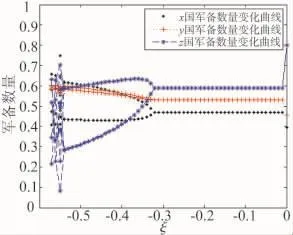
图3 ϑ=-0.1时三国军备竞赛随ξ变化的分叉图

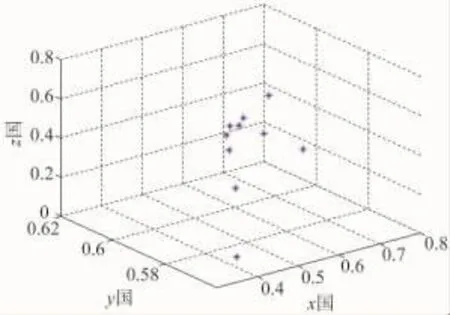
图4 混沌状态的吸引子

图4表示当ϑ=-0.1，ξ=-0.57时，三国军备竞赛处于混沌状态时的吸引子，此时军备竞赛处于极端的不稳定状态，各国为了取得最佳的利益，不断调整自己的装备数量，这也将造成其他国家的不安全感，并引发新一轮的军备竞赛，使地区局势动荡。图5～图7即为当国家x将军备数量从0.8改变为0.800 01时，三国军备数量的变化情况。

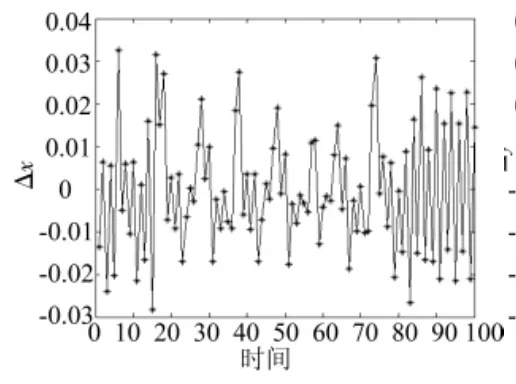
图5 国家x军备数量随时间变化情况

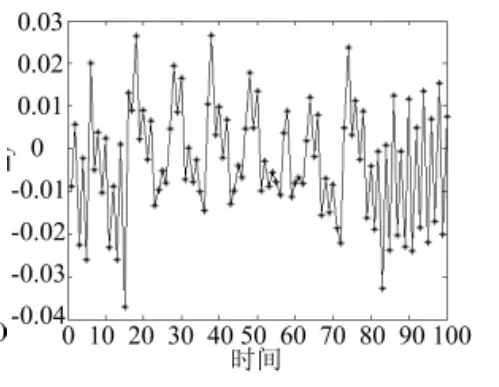
图6 国家y军备数量随时间变化情况

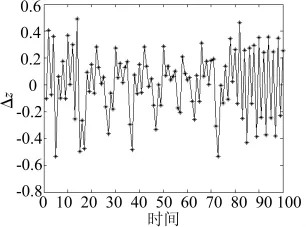
图7 国家z军备数量随时间变化情况

4 结论

军备竞赛中，各国的策略依据其他国家的军备情况而制定，而本国的做出的策略选择又将对下一时期其他国家的军备策略产生影响。军备竞赛的不稳定性，与各国采取不同的预期策略密切相关。本次研究发现，通过调整各国策略函数的预期取值，能够使三国军备竞赛从不稳定状态达到稳定状态，各国均没有改变他们策略的动机而使自身利益受损，这将有利于缓和地区局势，促进国际军控的发展和世界和平。

［1］魏伟.军备竞赛与裁军的博弈分析［J］.军事经济研究，2007，28（1）：18-20.

［2］骆桦，田晓军，周小红.单极世界军备竞赛微分方程稳定性的研究［J］.浙江理工大学学报， 2008，24（1）：103-105.

［3］刘光华，罗荣桂.基于博弈论的军备竞赛模型［J］.武汉理工大学学报，2006，28（10）：135-137.

［4］基斯.哈特利，托德.桑德勒.国防经济学手册［M］.北京：经济科学出版社，2001.

［5］杜清华.冷战后东南亚地图军备竞赛的经济学分析［J］.生产力研究，2011（11）：100-102.

［6］孙兆斌，曹少堔，郑凤云.民用经济与军事经济的趋同分析［J］.当代财经，2004（4）：14-16.

［7］浦小松.一类寡头垄断市场产量博弈及混合模型的动力学研究［D］.天津：天津大学，2012.

［8］廖晓昕.稳定性的理论、方法和应用［M］.武汉：华中科技大学出版社，2010.

［9］王翼.自动控制中的基础数学［M］.北京：科学出版社，1987.

Study on Dynamics of a Nonlinear Arms Race Game

ZHANG Zhi-pan1，2，YANG Ping-hua1
（1.Academy of Ordnance Engineering，Shijiazhuang 050003，China；
2.Chongzuo Military Subarea of Guangxi Military Region，Chongzuo 532200，China）

In allusion to the problem of multi-nation arms race，based on chaotic dynamical theory，and considering that the nonlinear factor affect arms race，the text adopted the quadratic equation to improved Richardson arms race model，founded a nonlinear three-nation arms race dynamical model.With Matlab we simulate a type of arms race and analyze results among different variables.The simulation result show that the anticipated function of game players affect stability of arms race.By adiusting variables of different anticipated functions，the state of arms race among nations take a stable turn from chaotic.The result will provide scientific indication for study on international arms control.

arms race，richardson model，chaotic，dynamics

E0-059

A

1002-0640（2015）03-0175-04

2014-01-18

2014-03-19

张志攀（1984- ）,男，四川成都人，硕士研究生。研究方向：博弈论及其军事应用。