L1正则化问题的对偶性理论*
2015-06-13吴焚供
吴焚供
(1. 华南师范大学数学科学学院,广州 广东 510631;2. 广东第二师范学院数学系,广州 广东 510303)
L1正则化问题的对偶性理论*
吴焚供1,2
(1. 华南师范大学数学科学学院,广州 广东 510631;2. 广东第二师范学院数学系,广州 广东 510303)
L1正则化问题是一个非光滑的无约束最优化问题,在变量选择,数据压缩和图像处理等领域有广泛的应用。给出了L1问题最优解存在的新的必要条件和充分条件,利用这些条件构造出L1正则化问题的一个Mond-Weir型对偶问题,最后给出了相应的弱对偶定理和强对偶定理。
L1正则化;最优解;对偶问题
正则化问题近年来备受关注,许多研究者考虑如下的Lp最小化问题
minF(x)=f(x)+ρ‖
其中f(x):Rn→R 为一光滑函数,ρ为一给定的非负正则化参数,p∈[0,1],变量x∈Rn,‖x‖p为定义在Rn上的Lp拟范数,当0 ‖ Lp正则化问题的一个重要的情况是如下的L2- Lp最小化问题 (1) 其中‖·‖为欧几里得范数,A∈Rm×n,m minF(x)=f(x)+ρ‖x‖1 (2) 该问题在文[7]和文[1]中分别被称为LASSO和BasisPursuit。他们证明了L1正则化问题与L0正则化问题在稀疏重建的意义下是等价的,从而L0正则化所要求的NP组合优化问题可以转化为L1罚优化问题。基于上述学者的工作,L1正则化成为当今数据分析的主流工具之一。 (3) 其中▽if(x)=∂f(x)/∂xi,sign(t)为符号函数。条件(3)在文[9]中被叙述为如下的等价形式在这些理论的基础上 x= sign (x-τ▽f(x))⊙ max{ |x-τ▽f(x)|-τρ,0} ,τ> 0 或 max{▽f(x)-ρ,min{x,▽f(x)+ρ}}=0 在这些理论的基础上,一些有效求解L1问题的算法得以建立,具体可参考文[9-11]等。 然而L1正则化问题毕竟是非光滑优化问题,若能构造出其光滑的对偶问题,则更有效的求解该问题便是有可能的。另一方面,早在1974年Mond[12]和1981年Mond和Weir[13]便考虑了一类特殊的不可微优化问题的对偶问题, 受其工作的启发,运用类似的方法构造出L1正则化问题的一个光滑的对偶问题,我们称之为Mond-Weir型对偶。 考虑原始问题(P) minF(x)=f(x)+ρ‖x‖1 证明 记S={y|y=▽f(x0)+ρw,wTx0=‖x0‖1,w∈Rn,|wi|≤1,i=1,2,…,n},若不存在w∈Rn使命题成立,则0∉S,由于S是闭凸集,根据凸集分离定理,存在z′∈Rn及α∈R,使得 z′Ty≤α<0,∀y∈S (4) 取w∈Rn,使得 这与假设Z0=Ø矛盾。 定理2(必要条件) 若x0是问题(P)的解,则存在w∈Rn,使得 ▽f(x0)+ρw=0 (5) (6) (7) 证明 若x0是问题(P)的解,则对任意给定的z∈Rn,及任意的实数α>0,有 F(x0+αz)-F(x0) = 两边除以α并令α→0+,则对任意的z∈Rn, 即Z0=Ø,所以由引理,定理结论成立。 定理3(充分条件) 若f为凸函数,且存在x0,w∈Rn使(x0,w)满足▽f(x0)+ρw=0及‖w‖1≤1,则x0是问题(P)的解。 证明 对任意的x∈Rn,由f(x)是凸函数,所以 F(x)-F(x0)=f(x)+ρ‖x‖1-f(x0)-ρ‖x0‖1≥ (x-x0)T▽f(x0)+ρ‖x‖1-ρ‖x0‖1 再由式(5)-(6)及xTw≤‖x‖1·‖w‖1,有 以下我们均假设f是凸函数,我们将建立起原问题(P)与如下问题(D)的对偶关系。 (D) maxG(u)=f(u)-uT▽f(u) s.t.▽f(u)+ρw=0 (8) ‖w‖1≤1 (9) 记问题(P)的可行域为ΩP,问题(D)的可行域为ΩD。 定理4(弱对偶定理) 问题(P)的下确界大于或等于问题(D)的上确界。 证明 对任意x∈ΩP,(u,w)∈ΩD, F(x)-G(u)=f(x)+ρ‖x‖1-f(u)+ uT▽f(u)≥(x-u)T▽f(u)+ρ‖x‖1+uT▽f(u) 根据式(8)-(9),有 F(x)-G(u)≥ρ(‖x‖1-xTw)≥0 所以结论成立。 定理5(强对偶定理) 若x0∈Rn是原问题(P)的一个最优解,则若存在w∈Rn,使(x0,w)∈ΩD,则(x0,w)必是问题(D)的解,且两问题的最值相等。 证明 若x0是问题(P)的解,则由定理2存在w使式(5)-(7)成立,而且有 ▽f(x0)= 再由定理4,只要(x0,w)∈ΩD,则(x0,w)∈ΩD必是(D)的解。 [1]CHENSS,DONOHODL,SAUNDERSMA.Atomicdecompositionbybasispursuit[J].SIAMJournalonScientificComputing, 1998, 20(1): 33-61. [2]CHARTRANDR.Exactreconstructionofsparsesignalsvianonconvexminimization[J].SignalProcessingLetters,IEEE, 2007, 14(10): 707-710. [3]CHARTRANDR,STANEVAV.Restrictedisometrypropertiesandnonconvexcompressivesensing[J].InverseProblems, 2008, 24(3): 035020. [4]CHENX,ZHOUW.Smoothingnonlinearconjugategradientmethodforimagerestorationusingnonsmoothnonconvexminimization[J].SIAMJournalonImagingSciences, 2010, 3(4): 765-790. [5]DONOHODL.Compressedsensing[J].InformationTheory,IEEETransactionson, 2006, 52(4): 1289-1306. [6]FANJ,LIR.Variableselectionvianonconcavepenalizedlikelihoodanditsoracleproperties[J].JournaloftheAmericanStatisticalAssociation, 2001, 96(456): 1348-1360. [7]TIBSHIRANIR.Regressionshrinkageandselectionviathelasso[J].JournaloftheRoyalStatisticalSociety:SeriesB(Methodological), 1996: 267-288. [8]CLARKEFH.Optimizationandnonsmoothanalysis[M].SIAM, 1990. [9]HALEET,YINW,ZHANGY.Fixed-pointcontinuationforl1-minimization:Methodologyandconvergence[J].SIAMJournalonOptimization, 2008, 19(3): 1107-1130. [10]SHEVADESK,KEERTHISS.Asimpleandefficientalgorithmforgeneselectionusingsparselogisticregression[J].Bioinformatics, 2003, 19(17): 2246-2253. [11]FUWJ.Penalizedregressions:thebridgeversusthelasso[J].JournalofComputationalandGraphicalStatistics, 1998, 7(3): 397-416. [12]BERTRAMM.Aclassofnondifferentiablemathematicalprogrammingproblems[J].JournalofMathematicalAnalysisandApplications,1974, 46:169-174. [13]MONDB,WEIRT.Generalizedconcavityandduality[C].GeneralizedConcavityinOptimizationandEconomics, 1981: 263-279. Duality Theorem forL1-Regularization Problem WUFengong1,2 (1. Department of Mathematics, South China Normal University, Guangzhou 510631, China; 2. Department of Mathematics, Guangdong University of Education, Guangzhou 510303, China) L1-regularizationproblemisanon-smoothunconstrainedoptimizationproblem,whichiswidelyusedinthefieldssuchasvariableselection,datacompressionandimageprocessing.OptimalityconditionsforthesolutionofL1-regularizationproblemisgiven.AndaMond-WeirtypedualproblemforL1-regularizationproblemisformulated,byusingtheseoptimalconditions.Finallyaweakdualitytheoremandastrongdualitytheoremareproved. L1-regularization;optimalitycondition;dualproblem 2014-03-07 广东省教育厅科研项目“育苗工程”(自然科学)资助项目(2013LYM_0061) 吴焚供(1980年生),男;研究方向:最优化算法理论;E-mail:wufengong@gdei.edu.cn 10.1347/j.cnki.acta.snus.2015.01.003 O A 0529-6579(2015)01-0010-03
1 最优性条件

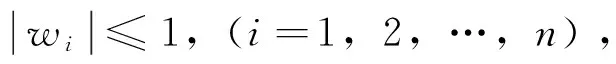

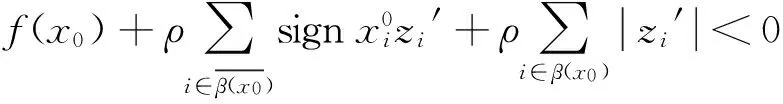
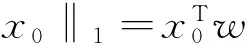
2 对偶性定理