一种带时间窗车辆路径问题的混合蚁群算法*

黄 震，罗中良，黄时慰

(惠州学院 计算机科学系，广东惠州，516007)



一种带时间窗车辆路径问题的混合蚁群算法*

黄 震，罗中良，黄时慰

(惠州学院 计算机科学系，广东惠州，516007)

针对带时间窗车辆路径问题求解时蚁群算法存在容易陷入局部最优，而遗传算法初始种群的优劣对算法有效性存在直接影响，提出一种混合蚁群优化算法。算法首先在蚁群算法的节点选择概率公式中引入时间窗因素，以得到初始种群，然后通过遗传算法的交叉算子和变异算子对初始种群中的较优路径进行交叉和变异操作，从而得到更优的路径。通过Matlab环境下对文中混合算法进行仿真实验，在车辆利用率和路径规划上效果明显，表明了算法的高效性，同时混合算法可以避免陷入局部最优。

蚁群算法；遗传算法；车辆路径问题；时间窗

车辆路径问题(Vehicle Routing Problem,VRP)是一类经典的组合优化问题。一般指对一系列的客户点组织适当的行车路线，使车辆有序地通过它们，在满足一定的约束条件(如货物需求量、车辆容量限制等)下，达到一定的目标(如距离最短、费用最少等)，带时间窗车辆路径问题(Vehicle Routing Problem with Time Windows,VRPTW)是在VRP的基础上要求在配送过程中按照客户要求在一定的时间窗内到达客户点，即在不违背车辆容量限制、时间限制等约束条件的前提下，合理制定运输时的车辆配送路径方案，以尽可能小的成本满足处在不同地理位置的客户对货物运送和服务时间的要求[1]。由于VRPTW带有服务时间的访问限制，VRPTW比VRP更贴近实际应用，广泛地应用于交通和物流领域，由于VRPTW是NP难问题，主要都是使用启发式算法[2-3]来求解，已有不少学者对该问题进行了相关的研究[4-11]。其中，李全亮[4]提出利用蚂蚁算法求解VRPTW，从数值计算上探索了蚂蚁算法的优化能力，获得了满意的效果；李琳等[5]将蚁群系统与最大最小蚂蚁系统相结合，并在状态转移规则中引入时间窗跨度与服务等待时间因素；何小锋等[6]提出一种量子蚁群算法，增加量子比特启发因子、利用量子旋转门实现信息素更新，实验表明该算法求解VRPTW比蚁群算法效率更高；吴天羿等[7]在初始种群的产生、交叉、变异等方面对遗传算法进行改进，在求解VRPTW中比遗传算法更有效。

本文首先使用蚁群算法求解VRPTW，实验结果发现蚁群算法存在容易陷入局部最优的缺点，于是将蚁群算法和遗传算法相结合，通过蚁群算法产生初始种群，然后进行交叉和变异操作，实验结果表明混合算法不仅可以避免陷入局部最优，而且具有比较快的收敛速度和良好的全局寻优能力，能够有效的求解VRPTW。

1 VRPTW的数学模型

VRPTW描述为[12]：某仓库有k辆车，每辆车的最大载重量为w，需要为n个客户配送货物， 其中仓库编号为0，客户编号为1至n，每辆车从仓库出发为客户送货，最终回到仓库，qi(i=1,2…,n)为各客户的货物需求量，ati表示车辆到达客户i的时间，wti表示车辆在客户i的等待时间，sti表示车辆在客户i的服务时间，tij表示车辆从客户i到客户j的行驶时间，[ei,li]是客户i的时间窗，即客户i的最早开始服务时间为左时间窗ei，最迟开始服务时间为右时间窗li，Cij为车辆从客户i到客户j的配送成本。

引入决策变量Xijk，其取值如下：

(1)

VRPTW的目标函数表示为：

(2)

一般情况下VRPTW的目标有2个，第一目标是配送的车辆数K最少，第二目标是总配送距离最短，所以需要在式(2)中将p1和p2的值设置为p1≫p2。

VRPTW的约束条件如下：

∀j∈{1,2,...,n}

(3)

(4)

(5)

(6)

(7)

ati≤li,∀i∈{1,2,...,n}

(8)

ei≤ati+wti≤li,∀i∈{1,2,...,n}

(9)

ati+wti+sti+tij+(1-xijk)p3≤atj

∀i,j∈{1,2,...,n},∀k∈{1,2,...,K}

(10)

wti=max{0,ei-ati},∀i∈{1,2,...,n}

(11)

ati≥0,∀i∈{1,2,...,n}

(12)

wti≥0,∀i∈{1,2,...,n}

(13)

sti≥0,∀i∈{1,2,...,n}

(14)

其中式(3)、(4)约束每个客户只由唯一车辆服务；式(5)是对仓库约束，即由仓库出发和回到仓库的车辆都是K辆；式(6)车辆的载重约束；式(7)为次回路消除条件，式(8)至式(14)是时间窗约束。

2 混合蚁群算法求解VRPTW

2.1 求解VRPTW的编码方式

本文在求解VRPTW时采用整数编码方式[13]，需要编码的包括初始种群的染色体个体和每个染色体对应的解路径，本文采用0表示仓库(有K辆车)，1至n表示客户编号，具体编码方式如下：

1)每个染色体个体采用一个n维整型向量[r1,r2,...,rn]表示，ri∈{1,2,…,n}，每个ri对应一个客户。

2)解路径采用一个n+K+1维的整型向量[t1,t2,...,t(n+K+1)]表示，tj∈{0,1,…,n}，每个tj对应仓库或客户。

每个染色体个体对应一个解路径，由染色体个体求解路径的基本原理是求出K条子路径，每条子路径对应一辆车的行驶回路，具体求解方法如下：

1)将解路径向量的第一维分量t1赋值为0，表示车辆由仓库出发；

2)定义变量Q(初始值为0)，将染色体个体中的客户r1的货物需求量加到Q中，如果Q不超过车辆的最大载重量则计算atr1(即从仓库到达客户r1的时间)，如果atr1没有超过客户r1的时间窗则将r1加入到解向量中(即将r1赋值给解路径向量的第二维t2)；

3)按步骤2类似的方法继续计算染色体个体向量中r1后面的每一个客户ri，如果满足重量约束和时间窗约束则将ri加入到解向量中，如果Q超重或者atr1超过时间窗则不把ri加入到解路径向量中，而是将仓库编号0加入到解路径向量中(表示车辆回到仓库)，这样在解路径向量中就构成了子路径1；

4)按照步骤2、3的方法遍历染色体个体向量中剩下的客户编号，可以求出所有子路径。

2.2 求解VRPTW的混合蚁群算法

算法的流程如图1所示。

图1 混合蚁群算法流程图Fig.1 Flow diagram of hybrid ant colony algorithm

2.2.1 蚁群算法产生新种群 首先采用的蚁群算法求解VRPTW的新种群，具体步骤如下。

1)设置蚂蚁数量(一般与客户数相同)，每只蚂蚁的节点选择概率如式(15)所示

(15)

其中τik是指边(i，k)上的信息素，ηik是指与边(i，k)相关的启发信息函数，一般取1/d(i,k)，d(i,k)为节点i与k之间的距离；α和β分别为信息素因子和启发因子，分别影响信息素和启发信息函数的重要程度。

Tik是时间窗信息函数，γ是时间窗信息因子，Tik计算方法如式(16)

(16)

waitj是车辆在节点j的等待时间，当车辆到达节点j的时间atj早于节点的左时间窗ej时，等待时间取值为ej-atj，若车辆到达时间晚于左时间窗ej且早于右时间窗lj则将等待时间设置为较小的数；lj-ej为节点j的时间窗跨度，在等待时间相同的情况下时间窗跨度越小的节点应该优先选择，由公式(16)可知，等待时间越短、时间窗跨度越小的节点选择概率越大，使得车辆配送的效率越高。

2)当蚂蚁从节点i选中节点j后，应该减少边(i,j)的信息素，这样可以增加蚂蚁选择其他节点的概率，本文按照式(17)更新边(i,j)上的信息素

τij=(1-ρ)τij+ρΔτij

Δτij=Q/lk

(17)

其中ρ∈[0,1]为信息素挥发系数，Q是信息素大小(通常取常数)，lk是指本次迭代中第k只蚂蚁已经走过的路径长度。

3)每只蚂蚁按照步骤1选择完所有节点后即产生一个染色体个体，所有蚂蚁产生的染色体个体构成初始群体。

2.2.2 计算适应值 产生了新种群后，需要计算各染色体个体对应的适应值，具体步骤如下。

1)各染色体个体按照2.1的方法求解对应的解路径；

2)解路径的子路径数量即配送需求的车辆数K，将各子路径的配送成本全部加起来求出总配送成本后，根据公式(2)计算出染色体个体的适应值；

3)比较各染色体对应的适应值，更新当代局部最小值lbest和全局最小值gbest。

2.2.3 交叉和变异操作 遗传算法的交叉操作可以提高算法的全局搜索能力，本文在蚁群算法产生的新种群中选取两个染色体个体作为父代进行交叉操作，进行交叉的父代个体选择方法如下。

1)选取当代局部最小值lbest作为第一个父代个体；

2)为了更有利于后代的进化效果，第二个父代需要选择与lbest有一定差异的个体[14]，具体做法是先随机选择一个染色体个体作为父代2，然后计算两个父代的适应值F1和F2以及当前迭代适应值的最大值Fmax和最小值Fmin，接着计算(F1-F2)/(Fmax-Fmin)的绝对值，如果结果大于给定的阈值则开始交叉操作，否则重新选择第二个父代。

按照上述方法选择了两个父代个体后，开始交叉操作，本文算法采用了部分匹配交叉算子，交叉操作具体步骤如下。

1)随机产生两个交叉位作为交叉区域；

2)将两个父代的交叉区域分别加入对方的末尾；

3)分别删除两个父代中与交叉区域相同的客户点即产生两个新的个体；

4)计算新个体的适应值，如果新个体更优则更新局部最小值lbest和全局最小值gbest。

例如，父代个体1为X=[3 1 8 4 2 6 7 5]，父代个体2为Y=[2 8 5 7 3 4 6 1]，随机产生两个交叉位分别为3和6，取出X的第3至第6位[8 4 2 6]作为交叉区域，Y的第3至第6位[5 7 3 4]作为交叉区域，将交叉区域加入到对方末尾后两个个体分别成为[3 1 8 4 2 6 7 5 5 7 3 4]和[2 8 5 7 3 4 6 1 8 4 2 6]，分别删除相同客户点后产生两个新个体为[1 8 2 6 5 7 3 4]和[5 7 3 1 8 4 2 6]。

变异操作相对交叉操作更简单，一般只需要将染色体个体中的某一位与另一位交换即可，通过变异可以提高算法的局部搜索能力，本文算法的变异操作的步骤如下。

1)选取当代局部最小值lbest作为变异的个体；

2)在lbest的两条不同子路径上分别产生1个变异位，计算两个变异位交换后的个体适应值，如果适应值更优则保留变异后的个体。

3)如果变异后的个体更优则更新局部最小值lbest和全局最小值gbest。

2.2.4 全局更新信息素 当一次迭代结束后，需要更新每条边的信息素，信息素按照式(18)的方法更新

(18)

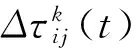
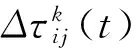
(19)

其中信息素大小Q为常数，Lk为第k只蚂蚁在本次迭代的路径总长度。

3 仿真实验

3.1 实验的参数设置

本文使用Matlab对算法进行仿真实验，其中蚁群算法的各参数设置为：α=1，β=5，γ=2，ρ=0.1，q0=0.7，Q=100；遗传算法的交叉概率设置为0.9，阈值设置为0.2，变异概率设置为0.2，求解目标函数时p1设置为10 000，p2设置为1。

3.2 实验及结果分析

3.2.1 实验1 实验1采用VRPTWBENCHMARKPROBLEMS测试集的数据，该测试集的数据分为C类(客户的地理位置集中分布)、R类(客户的地理位置随机分布)和RC类(客户的地理位置集中和随机相混合)3种数据集，本实验选取3类数据中有25个客户的C101-25、R101-25、RC101-25和有100个客户的C101-100、R101-100、RC101-100共6组数据，6组数据的理想解如表1所示。

表1 测试集的理想解Table 1 Optimal Solutions of the test problems

本文分别使用蚁群算法和本文算法进行10次仿真实验，25个客户的数据迭代次数为400次，100个客户的数据迭代次数为800次，蚁群算法和本文算法求出的最好解的结果如表2所示。

表2 实验1的仿真结果Table 2 Simulation results of the first experiment

由表2可知，本文算法在6组数据中无论在车辆数还是在配送的路径长度都明显优于蚁群算法的结果。在6组数据中，本文算法的都得到了理想解的车辆数，误差率均为0，而路径长度的误差率分别是0、0.1%、0.19%、0.43%、2.23%和4.61%，结果都非常接近理想解，其中C101-25得到了理想解，C101-25的配送路线如图2所示，图2中的X坐标和Y坐标是仓库和客户位置的坐标，路线图由3辆车配送，路径长度为191.813 6，由3条子路径构成，分别是0-5-3-7-8-10-11-9-6-4-2-1-0、0-20-24-25-23-22-21-0、0-13-17-18-19-15-16-14-12-0，其中0表示仓库号，1至25表示客户号。

图2 C101-25的车辆配送路线图Fig.2 Vehicle distribution routing for C101-25

3.2.2 实验2 为了更好的说明本文算法求解VRPTW的有效性，实验2采用文献[5]中的数据，实验数据包括1个仓库和20个客户，分布在边长为200km的正方形区域，仓库的坐标为145km,130km，每辆车的载重量为8t，车辆的行驶速度为60km/h，忽略车辆在客户点的服务时间，20个客户的具体数据如表3所示。

表3 客户的具体数据Table 3 Data of customers

文献[5]得到的最好解是3辆车进行配送，车辆利用率分别是96.25%、100%和100%，配送路径总长度为1 266.01km，本实验对上述数据进行仿真实验10次，实验的迭代次数400次，实验结果如表4所示。

表4 实验2的仿真结果Table 4 Simulation results of the second experiment

由表4可知，本文算法得到的最差解都比文献[5]的最好解的路径总长度更短，最好解的路径总长度为1 249.27km，对应的3条子路径分别是：0-7-8-15-16-13-20-0、0-5-14-4-3-17-11-0、0-18-1-10-2-12-9-19-6-0，车辆利用率分别是98.75%、97.5%和100%，实验表明本文算法的结果在同样使用3辆车配送的基础上，车辆的使用率更加平均，路径的总长度则更短。

4 结 论

本文将蚁群算法和遗传算法相结合来求解VRPTW，介绍了求解VRPTW的编码和解码方法、产生新种群的方法、交叉和变异以及全局更新信息素的方法。进行了两个仿真实验，实验1验证了本文算法在求解VRPTW时比基本蚁群算法更加有效，实验2表明本文算法比文献[5]的结果更优，说明本文算法是求解VPRTW的有效算法。

[1] 蒋波．基于遗传算法的带时间窗车辆路径优化问题研究[D]．北京：北京交通大学，2010．

[2] 罗中良,易明珠.最优化问题的蚁群混合差分进化算法研究[J].中山大学学报：自然科学版，2008，47(3)：37-41

[3] 罗中良,易明珠,唐华,等.开Y-开Δ变压器相序调整的蚁群优化方法及收敛性研究[J]．中山大学学报：自然科学版，2007，46(2)：29-32

[4] 李全亮．蚂蚁算法在带时间窗车辆路径问题中的应用研究[J]．数学的实践与认识，2006，36(10)：173-178．

[5] 李琳,刘士新,唐加福．改进的蚁群算法求解带时间窗的车辆路径问题[J]．控制与决策，2010，25(9)：1378-1382．

[6] 何小锋,马良．带时间窗车辆路径问题的量子蚁群算法[J]．系统工程理论与实践，2013，33(5)：1255-1261．

[7] 吴天羿，许继恒，刘建永，等．求解有硬时间窗车辆路径问题的改进遗传算法[J]．系统工程与电子技术，2014，36(4)：708-712．

[8] 袁建清.求解动态车辆调度问题的混合禁忌搜索算法[J].计算机应用与软件，2012，29(4)：148-150．

[9] 李进,傅培华．基于能耗的带时间窗车辆路径问题建模与仿真[J]．系统仿真学报，2013，25(6)：1147-1154．

[10] 王飞．带时间窗车辆调度问题的改进粒子群算法[J]．计算机工程与应用，2014，50(6)：226-229．

[11] 戚铭尧，张金金，任丽．基于时空聚类的带时间窗车辆路径规划算法[J]．计算机科学，2014，41(6)：218-221．

[12] 潘立军．带时间窗车辆路径问题及其算法研究[D]．长沙：中南大学，2012．

[13] 黄震．混合量子粒子群算法求解车辆路径问题[J]．计算机工程与应用，2013，49(24)：219-223．

[14] 周艳聪，孙晓晨，余伟翔．基于改进遗传算法的物流配送路径优化研究[J]．计算机工程与科学，2012，34(10)：118-122．

Application Research of Hybrid ant Colony Algorithm in Vehicle Routing Problem with Time Windows

HUANGZhen,LUOZhongliang,HUANGShiwei

(Department of Computer Science, Huizhou University, Huizhou 516007, China)

A hybrid ant colony algorithm was proposed.Because, ant colony algorithm used to solve the vehicle routing problem with time windows (VRPTW) is easy to fall into local optimum, and the quality of initial population in genetic algorithm affects the effectiveness of the algorithm directly. Firstly, the algorithm introduces the factors of time windows into node selection probability formula of ant colony algorithm to get the initial population. Secondly， the crossover and the mutation were operated to get a better path for the initial population. Applying Matlab environment for hybrid algorithm simulation, the effects on the vehicle utilization and path planning is obvious. It shows the algorithm is efficient, and can avoid falling into local optimum.

ant colony algorithm；genetic algorithm；vehicle routing problem；time window

2014-06-22

广东省科技计划资助项目(2012B010100038);广东省高等学校教学质量与改革工程本科类资助项目(粤高教函【2013】113号-113)、惠州市科技计划资助项目(A512.0234)、全国大学生创新训练资助项目(105771300)

黄震(1980年生 )，男；研究方向：智能算法、无线传感器网络;通讯作者:罗中良;E-mail:195146501@qq.com

10.1347/j.cnki.acta.snus.2015.01.009

TP301.6

A

0529-6579(2015)01-0041-06